Directx11教程(61) tessellation学习(3)

      现在我们看看在不同tess factor的情况下，三角形是如何细分的？(这儿三条边和内部tess factor值是一样的，而且partitioning("integer"))

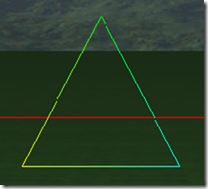
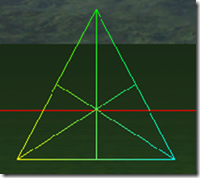
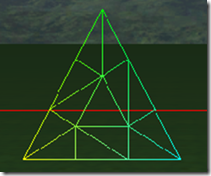
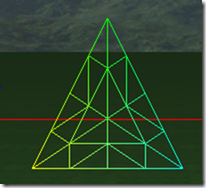
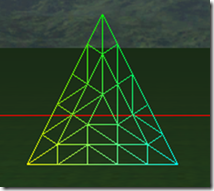
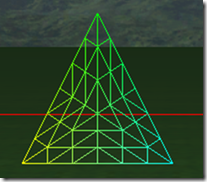
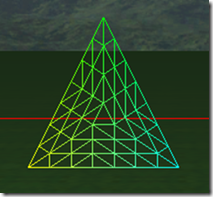
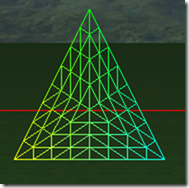
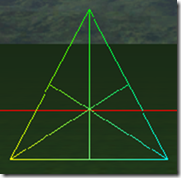
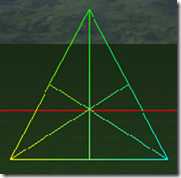
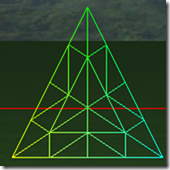
下面8张图是三角形在tess factor 1到8的情况下的细分细节：

 

     因为TS阶段是硬件自己做的，没有算法细节，所以我们只能从这些图中，来猜一猜不同tess factor情况下的规律。

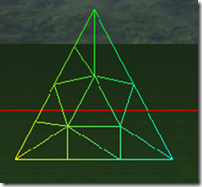
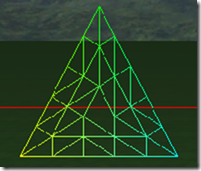
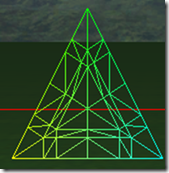
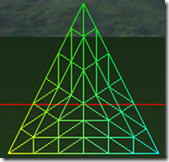
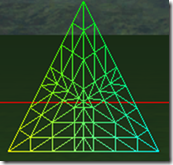
     可以看出在奇数的情况下，1, 3, 5, 7，…, 三角形包括(N+1)/2个环形的的三角形，而中心是一个三角形。在偶数的情况下，三角形内部包括N/2个环形的三角形，但中心是一个点，而不是一个三角形。三角形的边在tess factor 1-8的情况，分别被分为1-8段，对于内部的环形三角形，从外到内，每进一个层次，边分段数是是上一个边分段数减2，比如tess factor = 5,有三个环形三角形，最外边的边分段是5，中间的一个是3，最里面的是1。

     在tess factor 1-8的情况下，细分的三角形个数为：1, 6, 13, 24, 37, 54, 73, 96, 121, 150,有规律吗？

奇数tess factor：1， 13,   37， 73， 121， => 12, 24, 36,48,…(6*2, 6*4, 6*6, 6*8…)

偶数tess factor:6, 24, 54, 96, 150, => 18, 30, 42, 54, … (6*3, 6*5, 6*7, 6*9…)

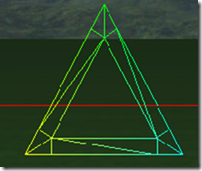
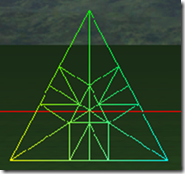
      每条边以及内部 tess factor也可以不一样，比如三条边的细分因子是2、3、4，内部细分因子是3，则三角形的细分如下图所示：

      从directx11 sdk上可以查到，Partitioning因子可以有四种，我们例子中用的是Integer,下面我们看看其它三种情况下，三角形的细分有什么变化。

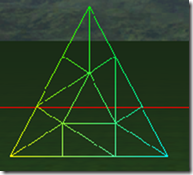
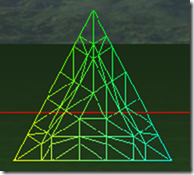
    fractional_odd表示tess factor是奇数，范围1..63, 此时细分效果和Integer是一样的，如果此时tess factor为偶数，则细分的效果很古怪。下面的就是fractional_odd的情况下，tess factor 1-8的戏份效果，偶数的细分并不均匀。

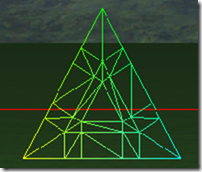
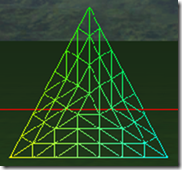
     fractional_even表示tess factor是偶数，范围是2-64，如果此时tess factor为1，则和2的结果是一样的，如果此时tess factor为奇数，则细分效果不均匀，下面的图是tess factor在1-8的情况下的细分效果：

 

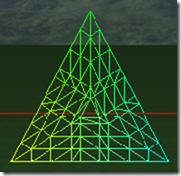
     pow2看字面意思，应该是2的幂次tess factor才有效，但是在我的卡(HD5760)上，细分效果和Integer是一样的。