verilog语法实例学习(11)

同步时序电路的一般形式

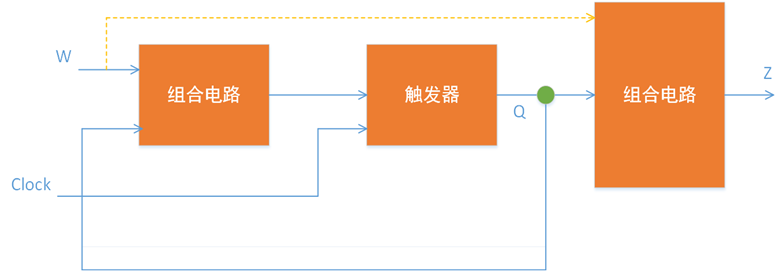
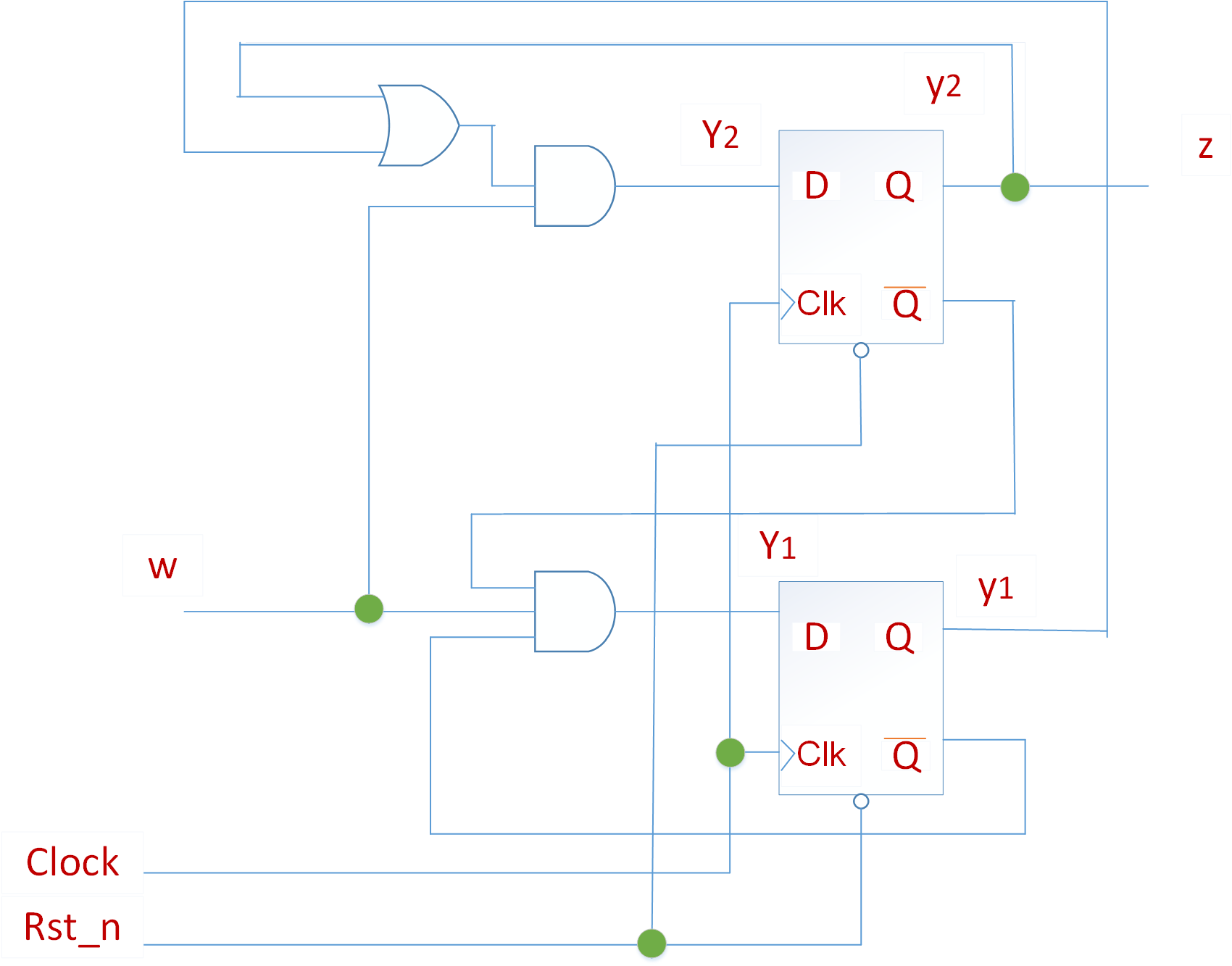
      时序电路由组合逻辑以及一个或多个触发器实现。一般的架构如下图所示：W为输入，Z为输出，触发器中存储的状态为Q。在时钟信号的控制下，触发器通过加在其输入端的组合逻辑输入，使得电路从一个状态变成另一个状态。采用边沿触发的触发器可以确保一个时钟周期内只发生一次状态变化。它们可以由时钟上升沿或下降沿触发，产生这种状态变化的时钟边沿称为有效时钟边沿。

      发器有两路组合逻辑输入，分别为原始输入W和触发器的当前输出Q，因此当前状态的改变不仅却决于触发器的当前状态，还取决于电路的原始输入。在上图中，可以得知，时序电路的输出由另一个组合电路产生，该组合电路是当前原始输入和触发器当前状态的函数。时序电路输出总取决于电路当前状态，却不一定直接依赖原始输入，图中的虚线表示可能存在也可能不存在。为了区分这两种存在，通常将输出仅由电路状态决定的时序电路称为Moore型，而输出由电路状态和原始输入共同决定的称为Mealy型。

摩尔有限状态机

      一个实际问题的描述：假设自动驾驶的汽车，以一定的速度运行，w=0，表示运行速度正常，w=1，表示运行超速。速度控制的策略，等间隔时间检测速度，如果两次或多次连续超速(w=1),则在一个时间间隔后开始设置减速信号z=1，否则z=0。如果用电路描述上述问题，则等时间间隔为时钟周期，在每个时钟的上升沿进行状态判断。输入输出信号时序序列如下：

时钟周期	t0	t1	t2	t3	t4	t5	t6	t7	t8	t9	t10
w	0	1	0	1	1	0	1	1	1	0	1
z	0	0	0	0	0	1	0	0	1	1	0

      我们用状态机来描述该问题：首先有一个起始状态A，电路加载或复位后为该状态。假设当前为A状态，如果w=0，不做任何事情，输出z=0，在时钟上升沿检测后，仍保持A状态，输出z=0，如果w=1，仍输出z=0，在下一个时钟周期边沿进入状态B，输出z=0；假设当前为B状态，如果w=0，输出z=0，在下一个时钟上升沿进入A状态，输出z=0，如果w=1，此时z输出仍为0，在下一个时钟上升沿，进入状态C，此时输出z=1；假设当前状态为C状态，如果w=0，此时仍有z=1，在下一个时钟上升沿进入A状态，此时输出z=0，如果w=1，在下一个时钟上升沿，仍操持状态C，输出z=1。

     该状态机的状态表如下：

现在状态	下一状态		输出 z
	w=0	w=1
A	A	B	0
B	A	C	0
C	A	C	1

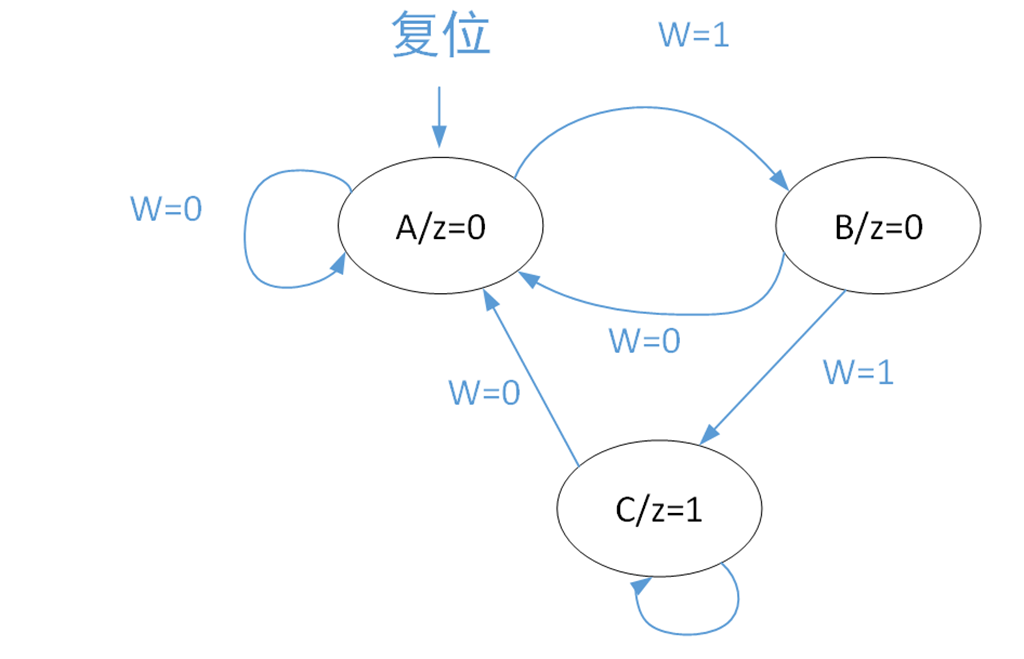
状态机状态图如下：复位信号强制电路进入A状态，任何条件下复位都成立，图中用箭头表示。

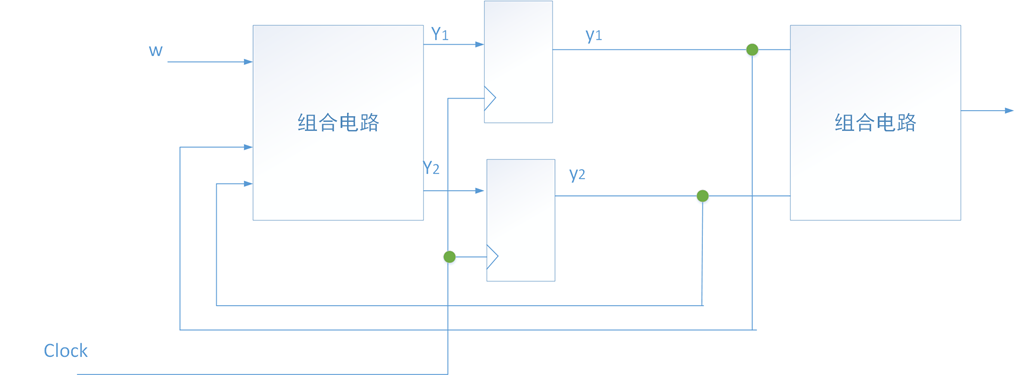
       上面的状态图和状态表中，我们用了3个状态A,B,C。在逻辑电路实现过程中，每个状态用状态变量的特定取值（值的组合）来表示。每个状态变量可能以触发器来实现。由于需要实现3种状态，因此采用2个状态变量就可以满足要求，令两个状态变量分别用y₁,y₂，来表示电路当前状态。另外用Y₁，Y₂表示下一状态，它由反馈电路和输入w决定。

从而，我们得到详细的状态赋值表。根据这个赋值表，我们能设计出具体电路，状态11在这个电路中没有使用。

	现在状态	下一状态		输出
		w=0	w=1
	y2y1	Y2Y1	Y2Y1	z
A	00	00	01	0
B	01	00	10	0
C	10	00	10	1
	11	dd	dd	d

Y₁的真值表

w/y2y1	00	01	11	10
0	0	0	d	0
1	1	0	d	0

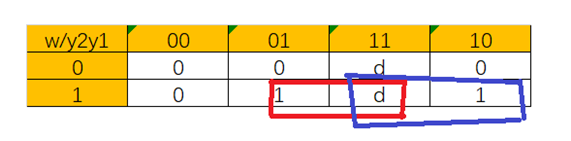
Y₂的真值表

w/y2y1	00	01	11	10
0	0	0	d	0
1	0	1	d	1

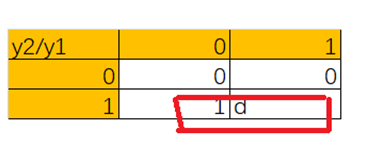
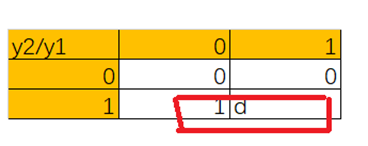
z的真值表

y2/y1	0	1
0	0	0
1	1	d

从上面赋值表中，我们能够得到下一个状态Y₁，Y₂的逻辑表达式为：

Y1=w~y₁~y₂

Y2=wy₁~y₂+w~y₁y₂(或w(y₁+y₂))

z=~y₁y₂(或z=y₂)

考虑11状态，可以画出卡诺图来简化电路，简化后的电路Y2和z如上面括号中的蓝色表达式。

状态机的verilog代码：

module moore(clk, w, Rst_n, z);

   input clk;   //时钟信号
	input w;
	input Rst_n; //复位信后
	output z;
   reg [1:0] y, Y; //现在的状态

	parameter A=2'b00,B=2'b01,C=2'b10;

	always @(w,y)
	begin
	  case(y)
	    A:
		    if(w==0) Y=A;
		    else Y=B;
		 B:
		    if(w==0) Y=A;
		    else Y=C;
	    C:
		    if(w==0) Y=A;
		    else Y=C;
	    default: Y=2'bxx;
	  endcase

	end

	always @(posedge clk,negedge Rst_n)
	begin
	  if(Rst_n==0)
	    y <= A;
	  else
	    y <= Y;
	end

	assign z=(y==C);
endmodule

testbench为：

`timescale 1ns/1ns
`define clock_period 20

module moore_tb;
  reg w;
  reg clk=1;
  reg Rst_n;
  wire z;


  moore moore0(.clk(clk),.w(w),.Rst_n(Rst_n),.z(z));
  always # (`clock_period/2) clk = ~clk;

  initial
  begin
    w = 1'b0;
	 Rst_n = 1'b1;
	 #(`clock_period)
	 Rst_n = 1'b0;
	 #(`clock_period)
	 Rst_n = 1'b1;
	 w = 1'b0;
	 #(`clock_period)
	 w = 1'b1;
	 #(`clock_period)
	 w = 1'b0;
	 #(`clock_period)
	 w = 1'b1;
	 #(`clock_period)
	 w = 1'b1;
	 #(`clock_period)
	 w = 1'b0;
	 #(`clock_period)
	 w = 1'b1;
	 #(`clock_period)
	 w = 1'b1;
	 #(`clock_period)
	 w = 1'b1;
	 #(`clock_period)
	 w = 1'b0;
	 #(`clock_period)
	 w = 1'b1;
	 #(`clock_period)
	 w = 1'b1;

	 #(`clock_period*20)
    $stop;
  end

endmodule

如果用2’b11表示状态C，则有下面的状态表：

	现在状态	下一状态		输出
		w=0	w=1
	y2y1	Y2Y1	Y2Y1	z
A	00	00	01	0
B	01	00	11	0
C	11	00	11	1
	10	dd	dd	d

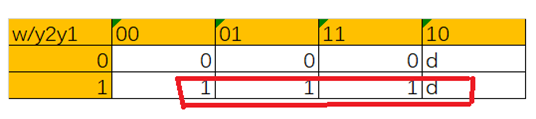
Y₁的真值表

w/y2y1	00	01	11	10
0	0	0	0	d
1	1	1	1	d

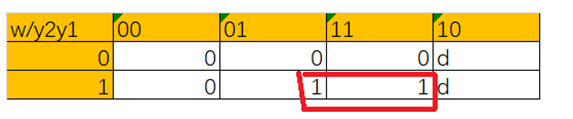
Y₂的真值表

w/y2y1	00	01	11	10
0	0	0	0	d
1	0	1	1	d

Z的真值表

y2/y1	0	1
0	0	0
1	1	d

用卡诺图简化输出表达式，

则有Y₁=w

Y₂=wy₁

z=y₂

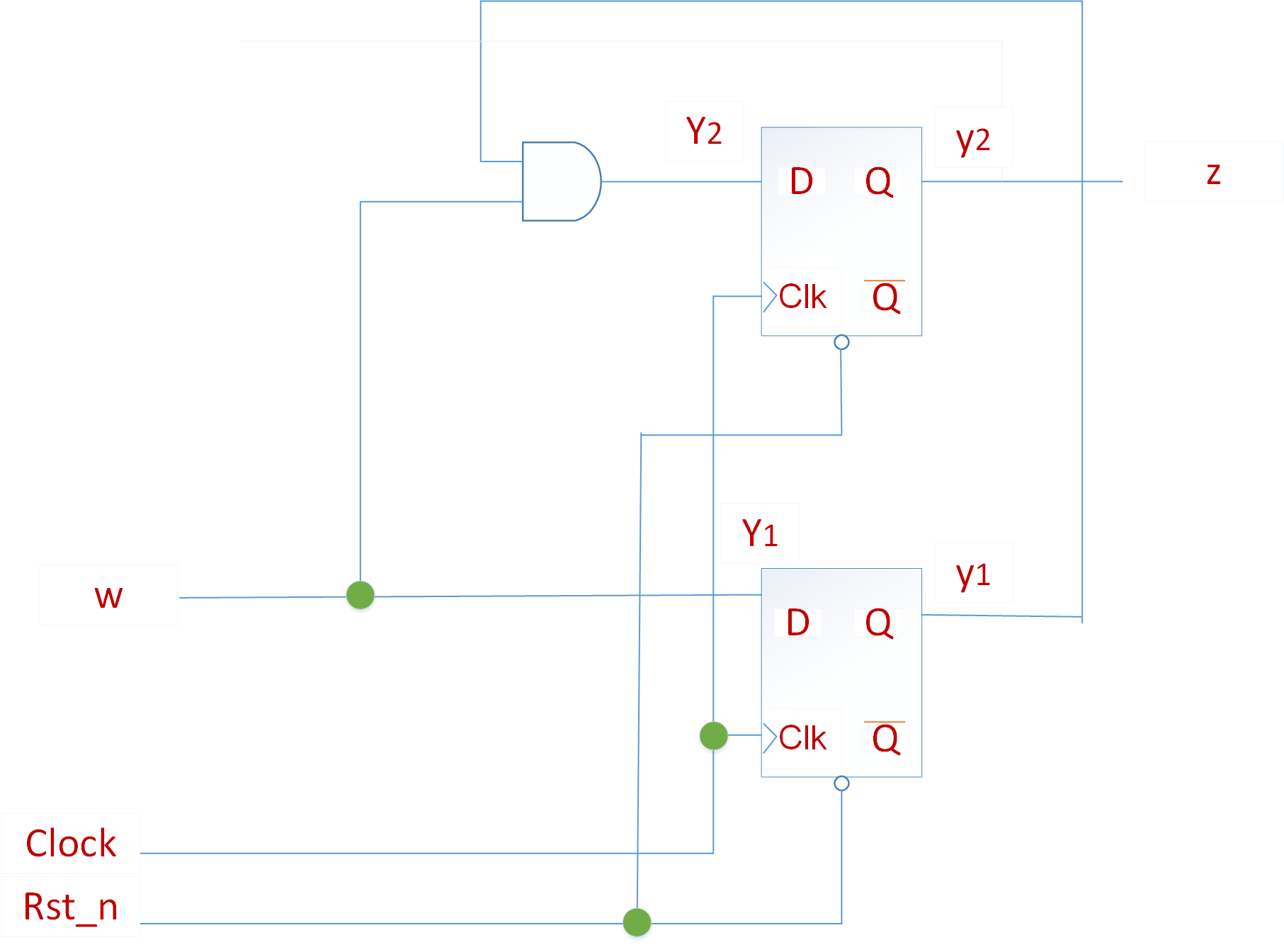
可以用下面更简化的电路实现：

假设用独热码表示状态A，B，C，则需要三位状态码，如下面的表格所示：

现在状态	下一状态		输出
	w=0	w=1
y3y2y1	Y3Y2Y1	Y3Y2Y1	z
001	001	010	0
010	001	100	0
100	001	100	1

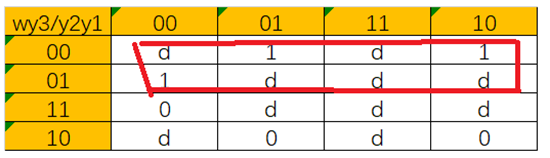
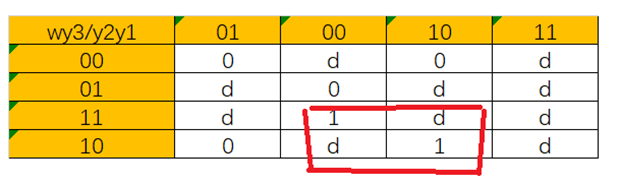
Y₁的真值表

wy3/y2y1	00	01	11	10
00	d	1	d	1
01	1	d	d	d
11	0	d	d	d
10	d	0	d	0

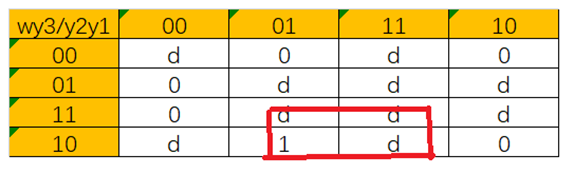
Y₂的真值表

wy3/y2y1	00	01	11	10
00	d	0	d	0
01	0	d	d	d
11	0	d	d	d
10	d	1	d	0

Y₃的真值表

wy3/y2y1	01	00	10	11
00	0	d	0	d
01	d	0	d	d
11	d	1	d	d
10	0	d	1	d

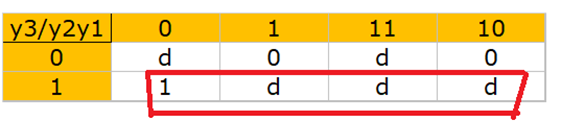
Z的真值表

y3/y2y1	00	01	11	10
0	d	0	d	0
1	1	d	d	d

用卡诺图简化输出表达式，所以有

Y₁=~w

Y₂=wy₁

Y₃=w~y₁

z=y₃

没有下一个状态与y₂有关，所以可以优化掉y₂触发器。

梅利有限状态机

一个实际问题的描述：假设前面自动驾驶的例子中，我们做一个修改，第二次检测到w=1的相同的周期内，z=1。输入输出信号时序序列如下：

时钟周期	t0	t1	t2	t3	t4	t5	t6	t7	t8	t9	t10
w	0	1	0	1	1	0	1	1	1	0	1
z	0	0	0	0	1	0	0	1	1	0	0

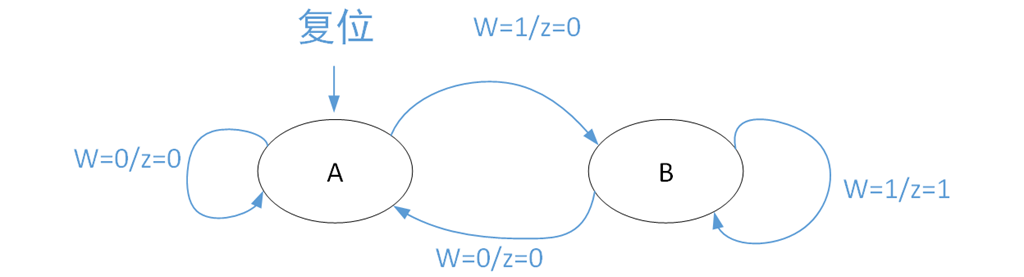
      我们用状态机来描述该问题：首先有一个起始状态A，电路加载或复位后为该状态。假设当前为A状态，如果w=0，输出z=0，如果w=1，输出z=0，在下一个时钟周期边沿进入状态B；假设当前为B状态，如果w=0，输出z=0，在下一个时钟上升沿进入A状态，如果w=1，输出z=1，在下一个时钟上升沿，仍保持状态B。

状态图如下：

该状态机的状态表如下：

现在状态	下一状态		输出 z
	w=0	w=1	w=0	w=1
A	A	B	0	0
B	A	B	1	1

状态分配表如下：

	现在状态	下一状态		输出 z
		w=0	w=1	w=0	w=1
	y	Y	Y	z	z
A	0	0	1	0	0
B	1	0	1	0	1

Y的真值表：

w/y	0	1
0	0	0
1	1	1

z的真值表：

w/y	0	1
0	0	0
1	0	1

Y=w

z=wy

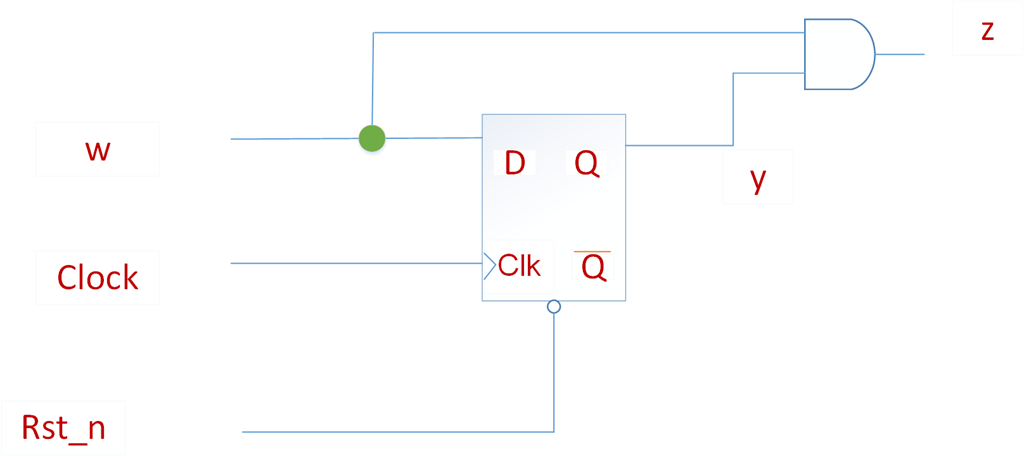
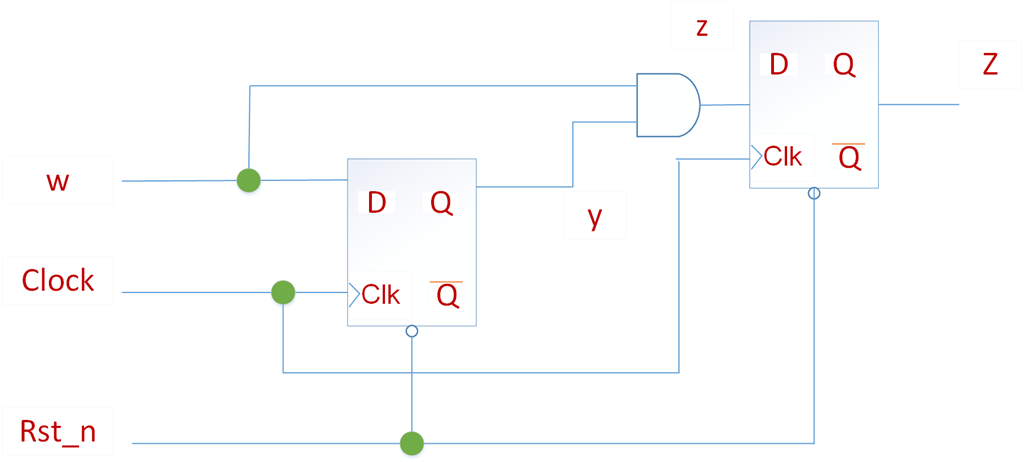
状态机的实现电路：

module mealy(clk, w, Rst_n, z);

   input clk;   //时钟信号
	input w;
	input Rst_n; //复位信后
	output  reg z;
   reg  y, Y; //现在的状态

	parameter A=1'b0,B=1'b1	;

	always @(w,y)
	begin
	  case(y)
	    A:
		    if(w==0)
			 begin
			    Y=A;
				 z=0;
			 end
			 else
			 begin
			    Y=B;
				 z=0;
			 end

		 B:
		    if(w==0)
			 begin
			    Y=A;
				 z=0;
			 end
			 else
			 begin
			    Y=B;
				 z=1;
			 end
	    //default: Y=1'bx;		 
	  endcase

	end

	always @(posedge clk,negedge Rst_n)
	begin
	  if(Rst_n==0)
	    y <= A;
	  else
	    y <= Y;
	end

endmodule

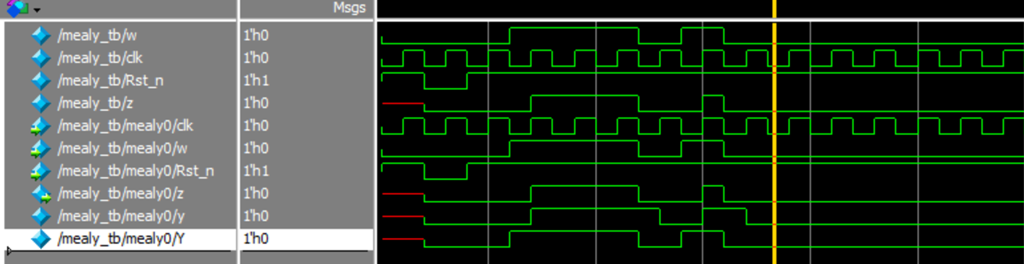
可以看到，相比moore型电路，mealy型电路更简单。另外从波形中，我们可以看到mealy型的电路输出z要比moore型早一个时钟周期。如果要得到和moore型一样时钟周期的输出，可以在mealy型实现电路上加一个触发器，打一拍，则可以得到和moore型一样的z输出时序。这时，mealy型也就转化成了对应的moore型电路。