verilog语法实例学习(10)
常用的时序电路介绍
T触发器和JK触发器
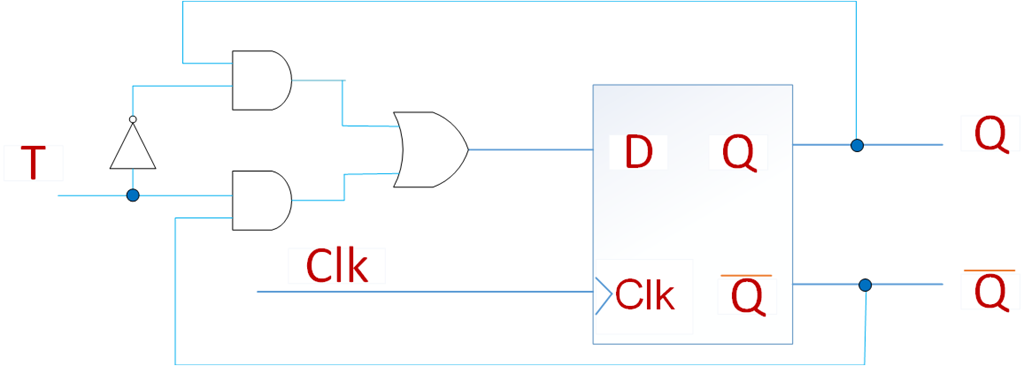
在D触发器输入端添加一些简单的逻辑电路,可以生成另一种类型的存储元件。比如下图所示的T触发器。该电路有一个上升沿触发的触发器和两个与门,一个或门,以及一个反相器组成。
在时钟上升沿到来之时,若T=0,则D=Q,若T=1,则D=~Q,因此,若T=0,在上升沿,电路保持当前状态,若T=1,则当前状态反转。
T触发器特性表图下,T触发器是构建计数器的一个有用元件。任何可以实现该特性的电路都可以称为T触发器。
| T | Q(t+1) |
| 0 | Q(t) |
| 1 | ~Q(t) |
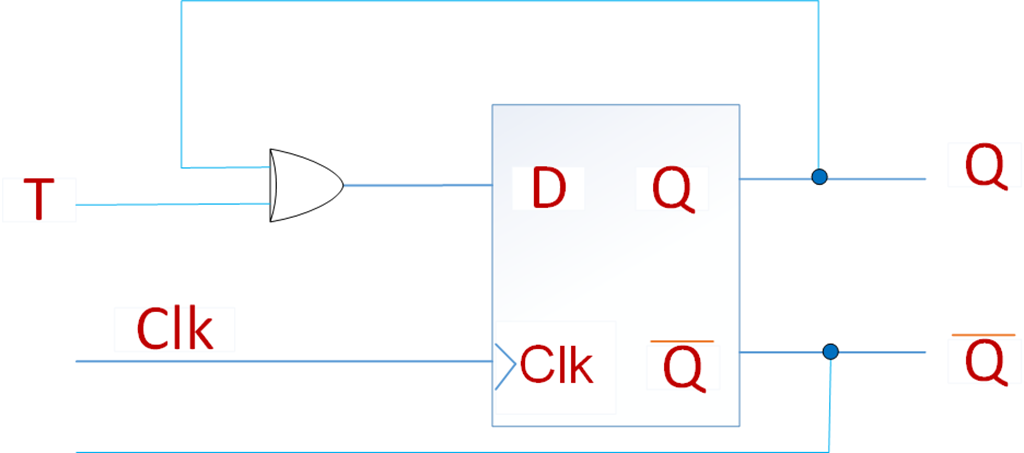
上述电路中D = ~T&Q+T&~Q=T^Q,所以我们也可以用下面的电路,通过一个异或门来实现T触发器。
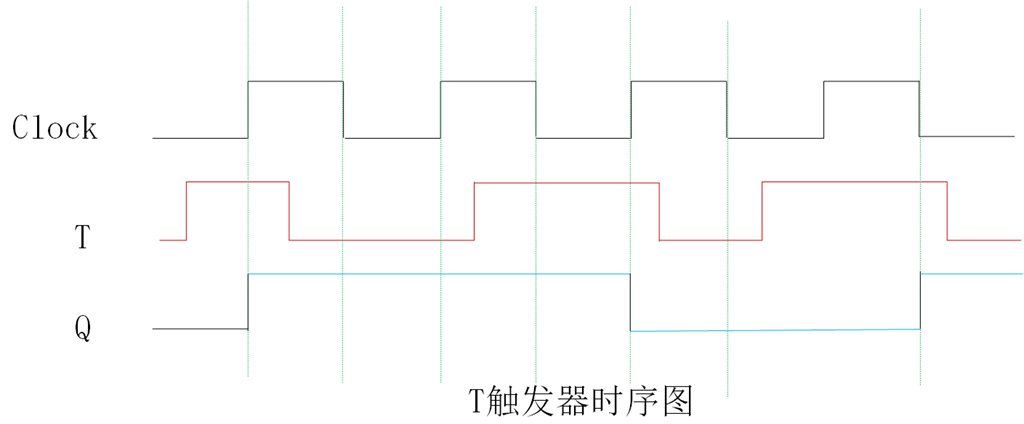
下面时T触发器的时序图:从图中,我们可以看到如果T=1,在时钟的上升沿,Q翻转信号值。
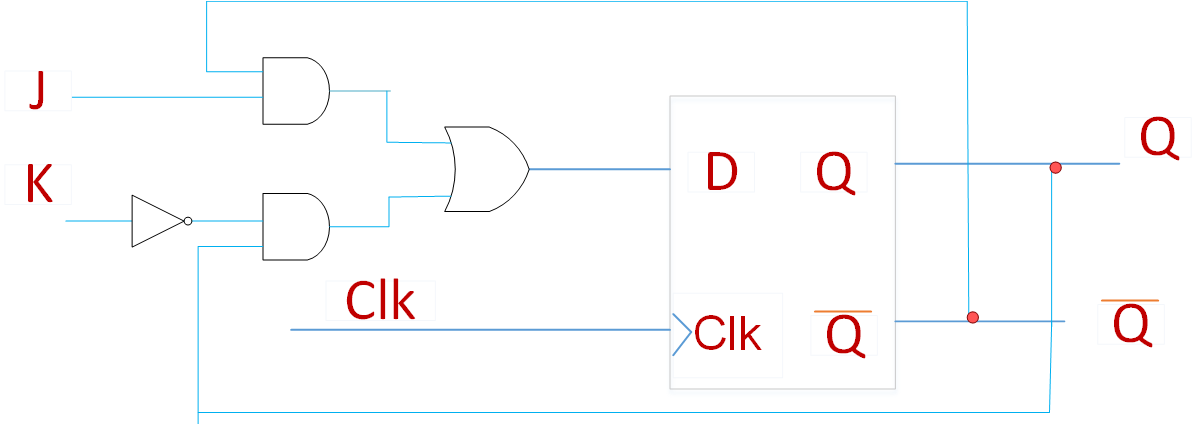
对T触发器进行一点改动,如下图所示,则形成另一个电路,该电路有两个输入,J,K。该电路中:D = J&(~Q)+~K&Q,它的特性表为:J=K,此时JK触发器等价于T触发器,J不等于K,该电路等价于SR触发器,此时S=J, R=K。D触发器是一种灵活的电路,可以像D触发器和SR触发器一样,存储数据,也可以把JK连接起来当T触发器使用。
| J | K | Q(t+1) |
| 0 | 0 | Q(t) |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | ~Q(t) |
计数器
计数器可以用加法减法器来实现,也可以用寄存器来实现。但由于计数器仅有+1,-1的变化,没必要采用复杂的电路。下面我们来学习用T触发器和D触发器构建的计数器电路。
T触发器构建的异步递增计数器
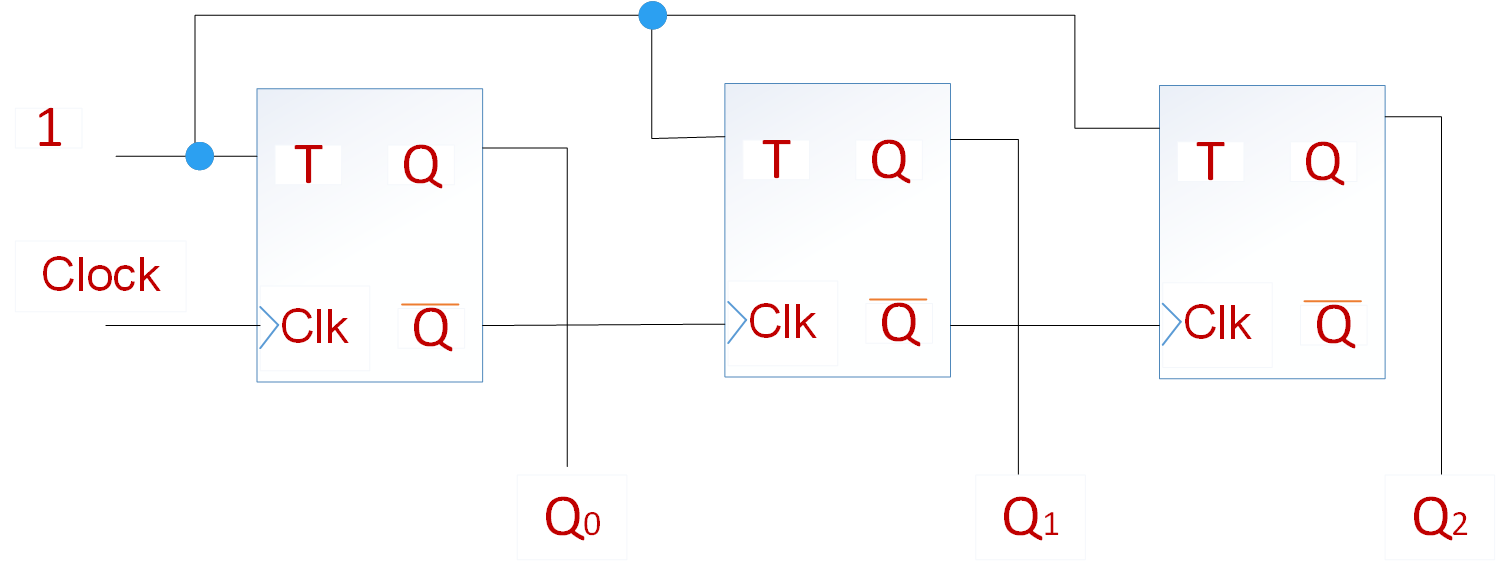
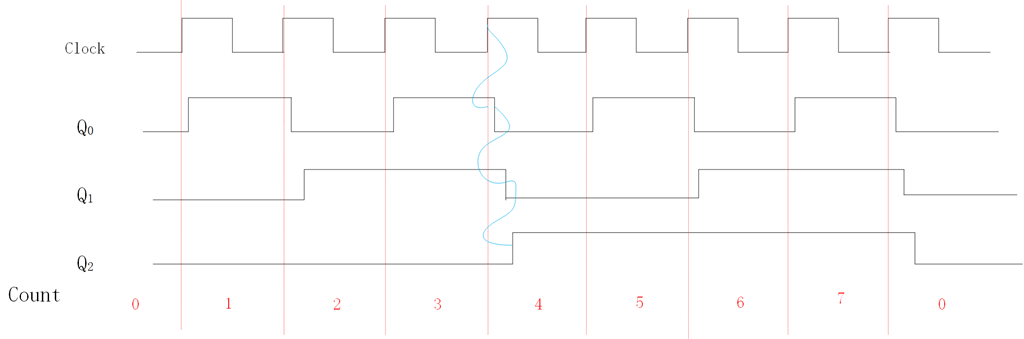
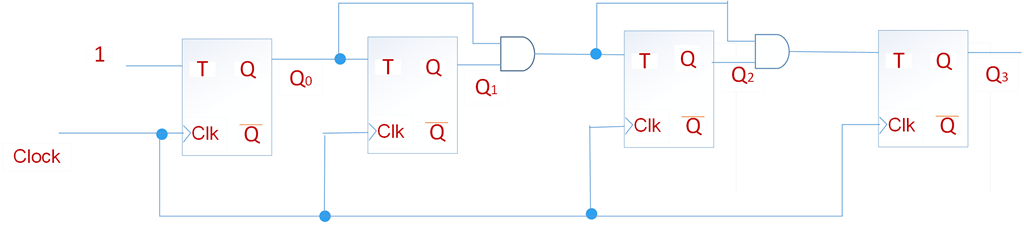
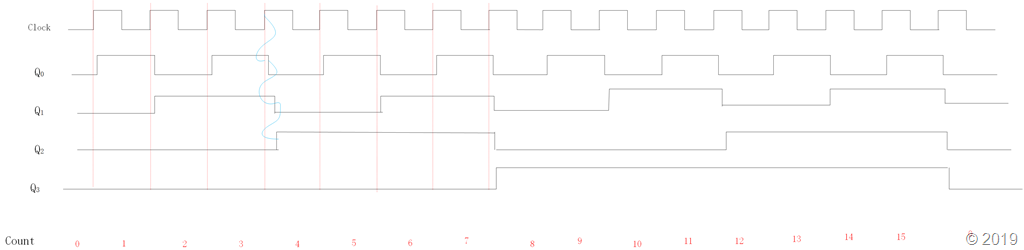
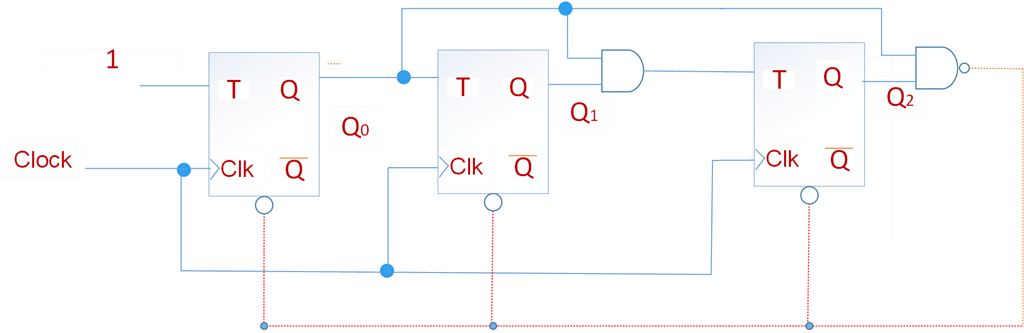
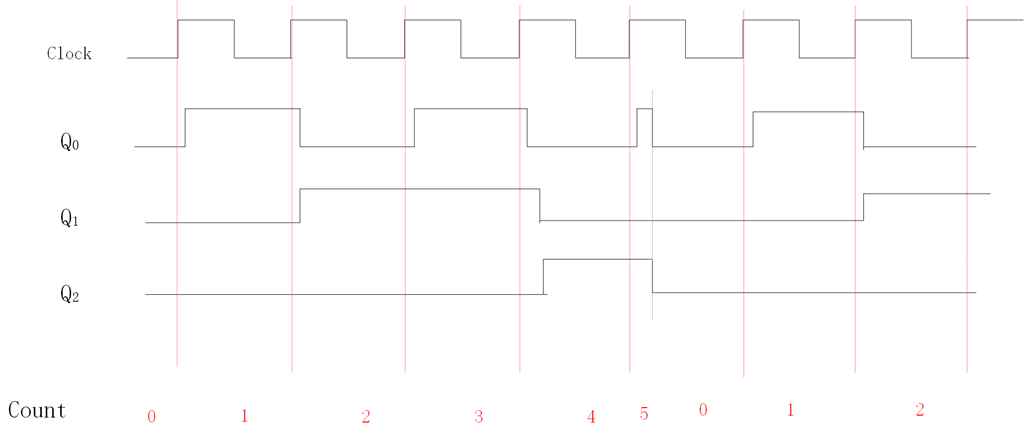
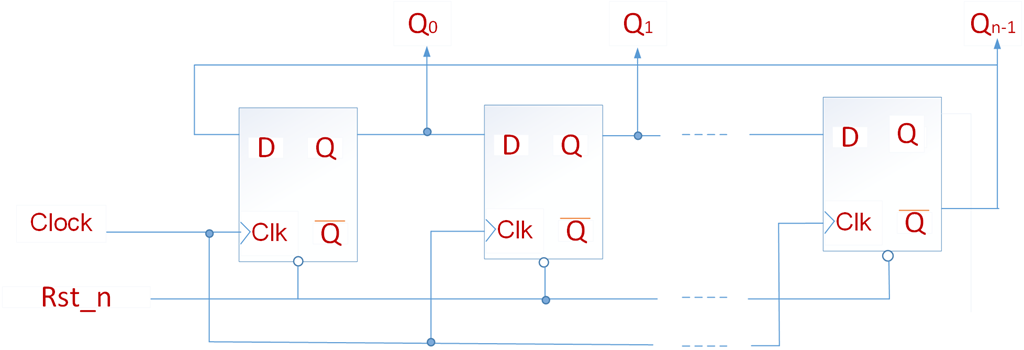
下图给出了一个3位的计数器电路,计数范围位0~7。三个触发器的时钟采用级联的方式连接。每个触发器的输入端T连接到逻辑电平1。触发器的状态在每个时钟的上升沿发生翻转。我们假设此电路的目的是对时钟脉冲的个数进行计数。如下面的时序图所示,每个时钟周期Q0状态变化一次,该变化发生在时钟上升沿稍后一点的时刻,延时是由于触发器的传输引起的。第二个触发器时钟信号为~Q0,所以Q1在Q0的下降沿稍后一点发生变化。同理,Q2在Q1的下降沿稍后一点发生变化。我们注意到Q2Q1Q0,其时序图为0,1,2,3,…,7,0, 1…等等,此电路是一个模8计数器,因为计数方式每次加1,所以为递增计数器。
因为时钟信号是级联的,而不是同步的,从时序图中可以看到在计数3和4之间,由那么一小段Q2Q1Q0=010(不稳定状态)
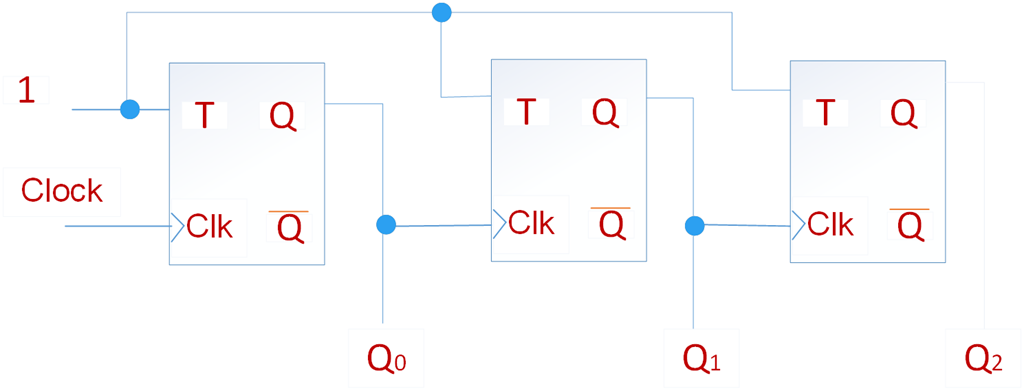
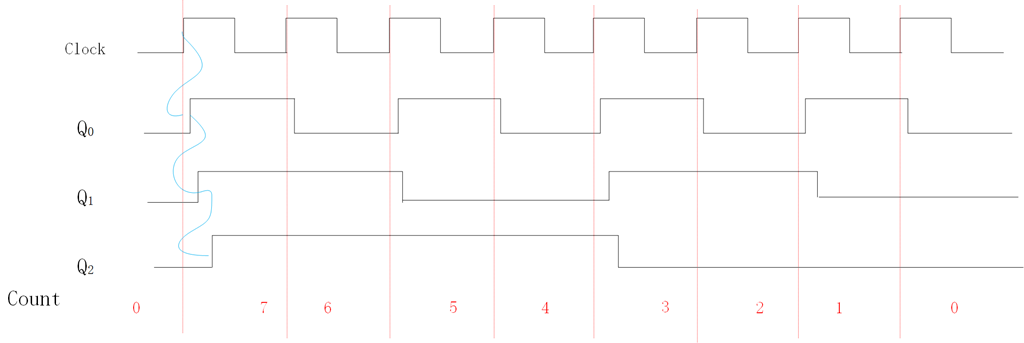
T触发器构建的异步递减计数器
采用下面的电路,我们可以得到递减计数器。和递增计数器的区别是Q1和Q2的时钟是接在输入Q,而不是~Q。
T触发器构建的同步递减计数器
上面构建的异步递增/递减计数器电路非常简单,但是运行速度不快。如果用这个电路构建多位计数器,由于时钟级联引起的延时可能会很长以至于不能满足所期望的性能要求。下面的方法,所有的触发器用同一时钟,可以构建一个速度更快的计数器。
下表是一个4位计数器在16个时钟周期内的内容。可以看到,Q0在每个时钟周期都要变化,Q1的状态仅在Q0=1时变化,Q2的状态仅在Q1,Q0都等于1时变化,Q3的状态仅在Q2,Q1,Q0都为1时候变化。一般来说,对于n位计数器,特定的触发器只在前面的触发器输出都为1时才发生变化。因此,用T触发器构建计数器,则输入端为:
T0=1
T1=Q0
T2=Q1Q0
T3=Q2Q1Q0
…
Tn=Qn-1 Qn-2…Q1Q0
| 时钟周期 | Q3 | Q2 | Q1 | Q0 | |
| 0 | 0 | 0 | 0 | 0 | |
| 1 | 0 | 0 | 0 | 1 | |
| 2 | 0 | 0 | 1 | 0 | Q1改变 |
| 3 | 0 | 0 | 1 | 1 | |
| 4 | 0 | 1 | 0 | 0 | Q2改变 |
| 5 | 0 | 1 | 0 | 1 | |
| 6 | 0 | 1 | 1 | 0 | |
| 7 | 0 | 1 | 1 | 1 | |
| 8 | 1 | 0 | 0 | 0 | Q3改变 |
| 9 | 1 | 0 | 0 | 1 | |
| 10 | 1 | 0 | 1 | 0 | |
| 11 | 1 | 0 | 1 | 1 | |
| 12 | 1 | 1 | 0 | 0 | |
| 13 | 1 | 1 | 0 | 1 | |
| 14 | 1 | 1 | 1 | 0 | |
| 15 | 1 | 1 | 1 | 1 |
用上面表达式构建的4位计数器电路图如下:
Q0的的输出要经过两个与门的延时才能到达Q3,这个延时必须小于时钟周期减触发器的建立时间。
下面是该电路的时序图,由于所有信号在时钟上升沿经过相同延时后发生变化,所以该电路为同步计数器。
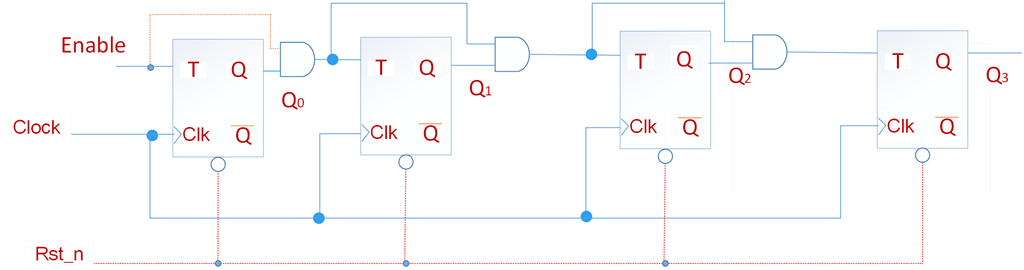
下面是带复位和使能信号的计数器,使能信号直接接在Q0输入端,如果Enable=0,则计数器不会计数,如果Enable=1,则和上面的计数器电路是一样的。复位信号在其的下降沿复位所有的触发器。
D触发器构建的同步计数器
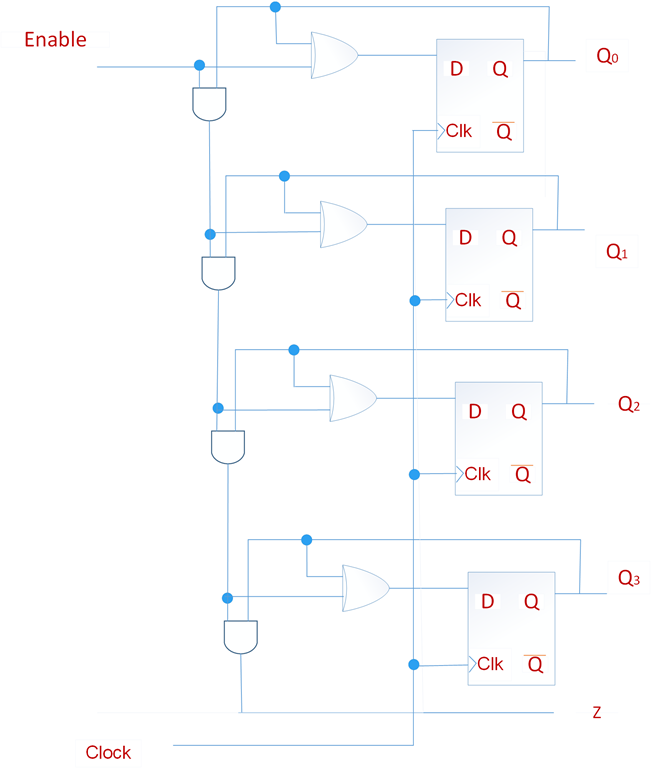
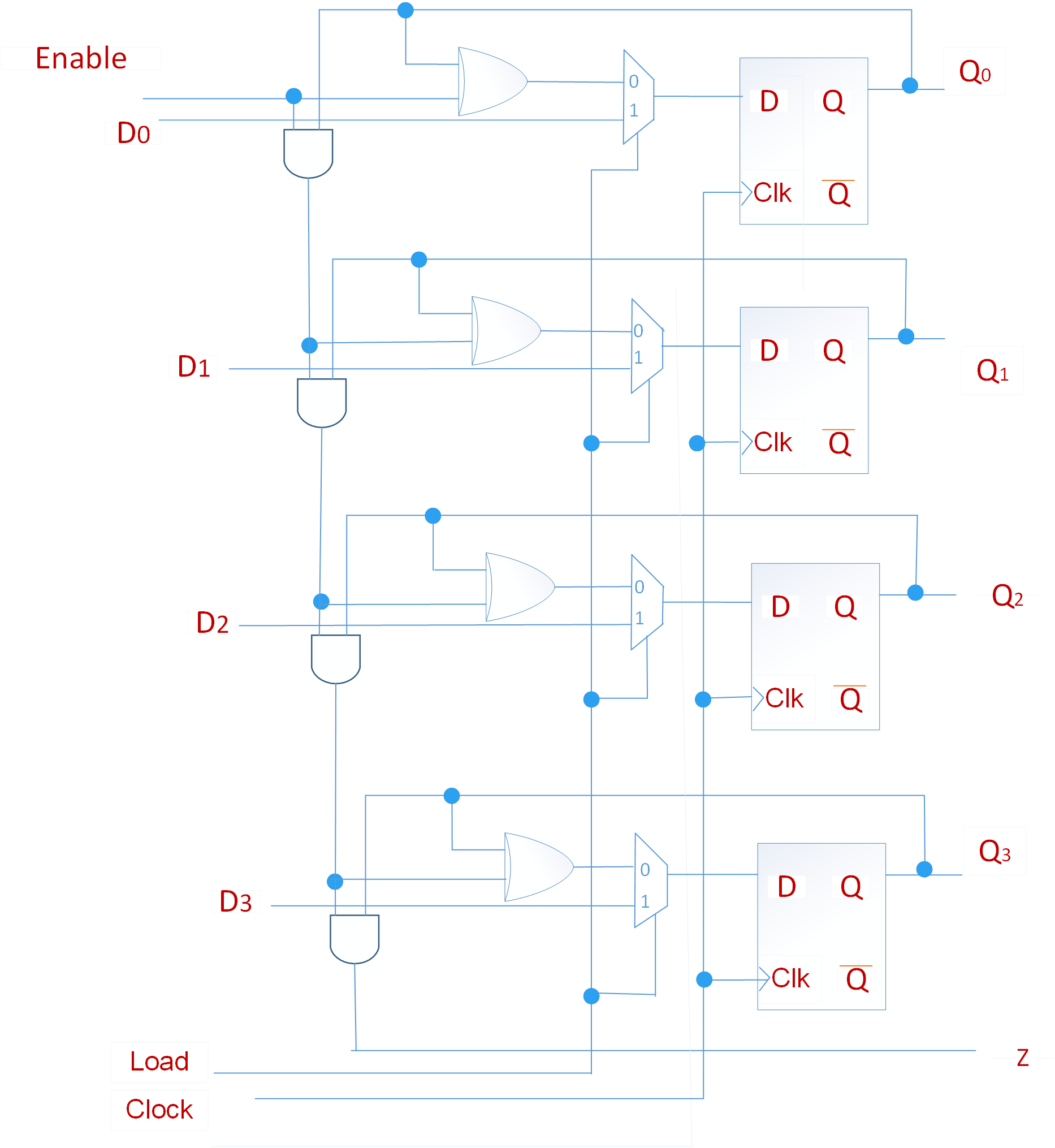
下面的电路结构是D触发器构成的4位同步计数器,计步顺序是0,1,2,…,15,0,1…计数值由触发器的输出端Q3Q2Q1Q0给出,假设使能端Enable=1,则计数器输入端由下面的表达式给出:
D0=Q0=Q0^1
D1=Q1^Q0
D2 = Q2^(Q1&Q0)
D3 = Q3^(Q2&Q1&Q0)
…
Dn=Qn^(Qn-1&Qn-2…Q1&Q0)
公式的推导: to do
加上Enable信号,公式为:
D0=Q0=Q0^Enable
D1=Q1^(Q0& Enable)
D2 = Q2^(Q1&Q0& Enable)
D3 = Q3^(Q2&Q1&Q0& Enable)
…
Dn=Qn^(Qn-1&Qn-2…Q1&Q0& Enable)
由下面的表格可知,第i级触发器的状态只有在它前面所有的触发器都处于Q=1的状态时候才改变。在此状况下,与第i级异或门相连的与门输出都为1,与Di相连的异或门输出为~Qi(与1异或,得到反值),否则或门的输出将使Di=Q,从而使该触发器保持原状态。
| 钟周期 | Q3 | Q2 | Q1 | Q0 | |
| 0 | 0 | 0 | 0 | 0 | |
| 1 | 0 | 0 | 0 | 1 | |
| 2 | 0 | 0 | 1 | 0 | Q1改变 |
| 3 | 0 | 0 | 1 | 1 | |
| 4 | 0 | 1 | 0 | 0 | Q2改变 |
| 5 | 0 | 1 | 0 | 1 | |
| 6 | 0 | 1 | 1 | 0 | |
| 7 | 0 | 1 | 1 | 1 | |
| 8 | 1 | 0 | 0 | 0 | Q3改变 |
| 9 | 1 | 0 | 0 | 1 | |
| 10 | 1 | 0 | 1 | 0 | |
| 11 | 1 | 0 | 1 | 1 | |
| 12 | 1 | 1 | 0 | 0 | |
| 13 | 1 | 1 | 0 | 1 | |
| 14 | 1 | 1 | 1 | 0 | |
| 15 | 1 | 1 | 1 | 1 |
我们增加一个额外的与门以产生输出Z,由于这个输出的存在,可以很容易的把两个4位计数器拼接成一个更大的计数器;同时这个输出还可用于检测计数是否达到了最大值(全部为1)。如果达到了则在下一个时钟周期进行清零。这在实际应用中也是十分有用的。
下面的电路本质上和上面T触发器构成同步计数器是相同的。增加一些电路,可以把D触发器改造成T触发器,D=Q^T,也实现了一个T触发器,
推导:to do
具有并行加载功能的计数器
把上面的电路进行一点小改动,加入一个二路选择器,用Load信号作为选择器的sel信号,来控制是载入还是计数功能。Load=1,并行载入一个计数值,Load=0,正常的计数功能。
同步复位与异步复位
计数器必须有清零的功能,在开始计数前其内容必须置0或复位。通过添加单个触发器的清零功能便可以达到此目的。但是对于在正常计数过程中如何使计数器的内容清零呢?n位的递增计数器使模为2n的计数器。如何得到不是2的幂的计数器呢?例如,模是6的计数器,它的计数序列是0,1,2,3,4,5,0,1等等。
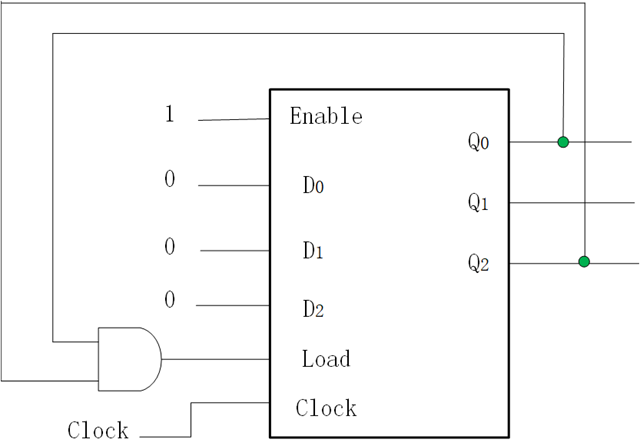
最直接的方法就是计数到5时候复位。可以通过探测Q2=Q0=1就够了,因为只有计数器等于5时,才有Q2=Q0=1。基于这种方法的电路如下图所示。计数器的并行加载功能用于在计数器达到5时使计数器复位。
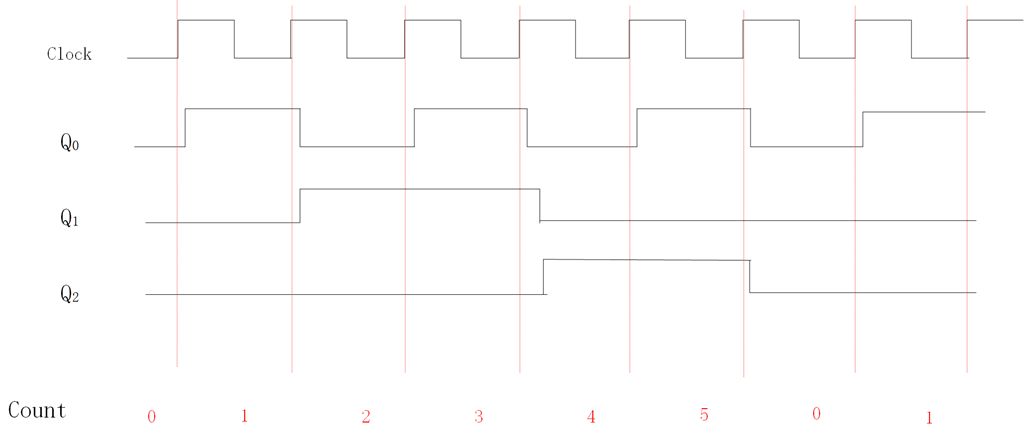
从下面时序图看出,复位的操作发生在计数到5后的时钟上升沿,它把D2D1D0=000加载到计数器,同时计数器的值在一个完整的时钟周期内建立起来获得期望的序列。
下面的电路通过触发器的特性实现清零。因为触发器的清零是低电平有效,所以可以用与非门检测计数值是否为5,如为5,则复位所有的触发器清零。从原理上看,该电路可以正常工作,但该电路存在隐患。当计数值等于5时,电路就会出现问题,因为只要计数等于5,与非门就会触发复位行为,触发器在与非门检测到5后很短时间内就使计数器清零,计数器等于5的时间依赖于电路的延迟而不是时钟,所以计数器等于5的时间很短,远小于一个时钟周期,在某些应用中,可能不能满足要求。这种复位称作异步复位。相比较起来,同步复位方案要比异步复位方案好。
其它类型的计数器
下面来看其它几种常用的计数器,第一中使用十进制序列,另外两种产生非二进制的代码序列。
BCD(二-十进制)计数器
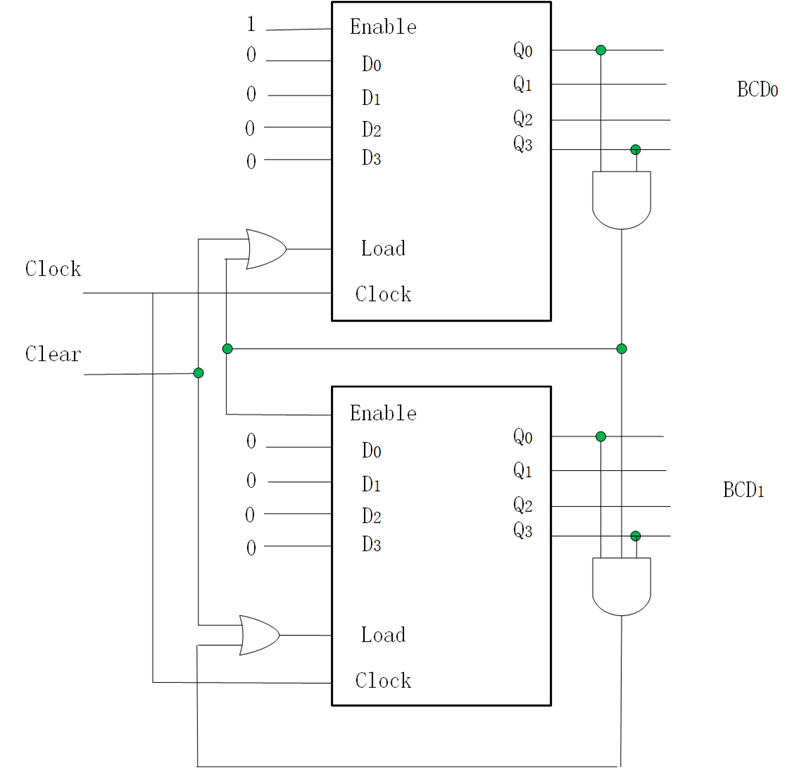
下面是一个二位的BCD码计数器,有两个模10的计数器组成。在模10计数器中,当计数器达到9时,必须将4个触发器复位,于是当Q3=Q0=1时,值Load=1,在时钟的下一个上升沿,将0000装入触发器。第一级的BCD0计数器的输入Enable一直为1,第二级的BCD1的输入Enable只有在第一级BCD0=9时候才为1,使下一个时钟脉冲到来时候,BCD1加1。实际电路中,有一个Clear控制信号控制清零,在下面电路中,Clear为高电平有效。
环形计数器
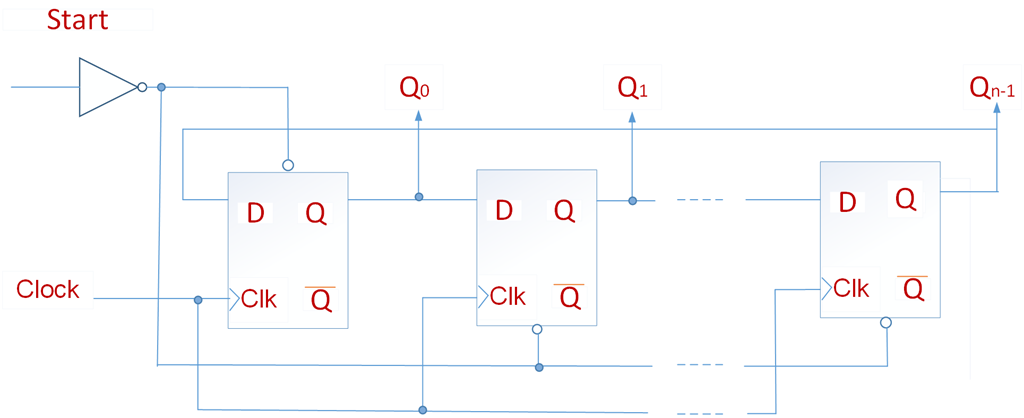
前面的计数器计数值都是一个二进制数。使用这种计数器时候,如果期望达到某个特定值时候产生一个动作,则必须检测这个计数值是否达到,这可以用与门实现。还有一些特殊的计数器,比如下图移位寄存器电路实现的四位环形计数器。start信号等于1向第一个触发器中置入1,而其它触发器中清零来设置初始值位100…00,start信号等于0,计数器正常计数。start信号的所有变化发生在时钟有效沿之后,以免违反触发器的时序参数。每个计数值都是一个独热码,编码中只有一个1,其它为0。
Johnson计数器
Johnson计数器如下图所示,它的反馈是~Q,n位的Johnson计数器可以产生2n位的计数序列。例如:4位的Johnson计数器的计数序列为0000,1000,1100,1110,1111,0111,0011,0001,0000,1000,…,为了对Johnson计数器进行初始化,必须使所有的触发器复位。不管是Johnson计数器还是环形计数器,如果初始化有错,都不能产生所期望的计数序列。
计数器verilog实现
有并行载入功能的递增计数器
verilog代码如下:
module upncount(R,Rst_n,clk,E,L,Q);
parameter n=8;
input [n-1:0] R;
input Rst_n;
input clk;
input E;
input L;
output reg [n-1:0] Q;
always @(posedge clk, negedge Rst_n)
begin
if(!Rst_n)
Q <= 0;
else if(L)
Q <= R;
else if(E)
Q<= Q + 1;
end
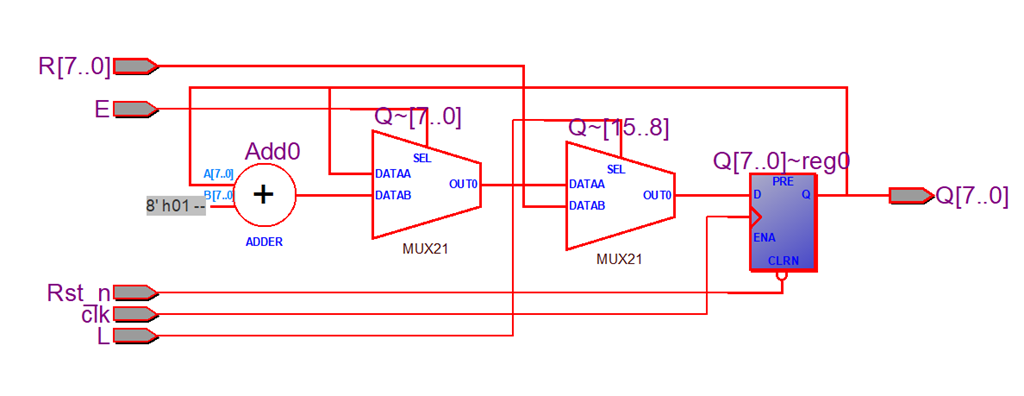
endmodule这些代码在quartus II综合与分析后,电路如下:一个加法器,两个二路选择器一个8位的寄存器。
用下面的testbench,可以得到如下波形。
`timescale 1ns/1ns `define clock_period 20 module upncount_tb; reg clk; reg Rst_n; reg [7:0] R; reg L; reg E; wire [7:0] Q; upncount #(.n(8)) upncount0(.R(R),.Rst_n(Rst_n),.clk(clk),.E(E),.L(L),.Q(Q)); initial clk = 1; always #(`clock_period/2) clk = ~clk; initial begin Rst_n = 1'b1; E= 1'b1; L=1'b0; R=8'd99; #(`clock_period) Rst_n = 1'b0; #(`clock_period) Rst_n = 1'b1; #(`clock_period*10); L = 1'b1; #(`clock_period); L = 1'b0; #(`clock_period*20); #2000; $stop; end endmodule
有并行载入功能的递减计数器
代码和波形如下:
module downncount(R,clk,E,L,Q);
parameter n=8;
input [n-1:0] R;
input clk;
input E;
input L;
output reg [n-1:0] Q;
always @(posedge clk)
begin
if(L)
Q <= R;
else if(E)
Q<= Q - 1;
end
endmodule`timescale 1ns/1ns `define clock_period 20 module downncount_tb; reg clk; reg [7:0] R; reg L; reg E; wire [7:0] Q; downncount #(.n(8)) downncount0(.R(R),.clk(clk),.E(E),.L(L),.Q(Q)); initial clk = 1; always #(`clock_period/2) clk = ~clk; initial begin E= 1'b1; L=1'b0; R=8'd99; #(`clock_period*10); L = 1'b1; #(`clock_period); L = 1'b0; #(`clock_period*20); #2000; $stop; end endmodule





 浙公网安备 33010602011771号
浙公网安备 33010602011771号