数据库索引的实现原理
数据库索引,是数据库管理系统中一个排序的数据结构,以协助快速查询、更新数据库表中数据。索引的实现通常使用B_TREE。B_TREE索引加速了数据访问,因为存储引擎不会再去扫描整张表得到需要的数据;相反,它从根节点开始,根节点保存了子节点的指针,存储引擎会根据指针快速寻找数据。

这张图不错
上图显示了一种索引方式。左边是数据库中的数据表,有col1和col2两个字段,一共有15条记录;右边是以col2列为索引列的B_TREE索引,每个节点包含索引的键值和对应数据表地址的指针,这样就可以都过B_TREE在O(logn)的时间复杂度内获取相应的数据,这样明显地加快了检索的速度。
==============================================================================================================================
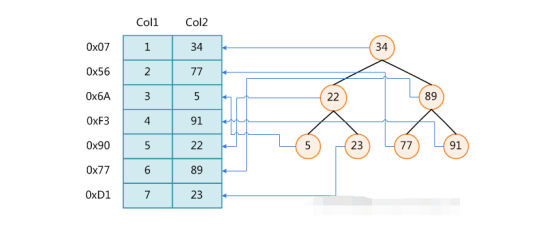
数据库索引,是数据库管理系统中一个排序的数据结构,以协助快速查询、更新数据库表中数据。索引的实现通常使用 B 树及其变种 B+ 树。
在数据之外,数据库系统还维护着满足特定查找算法的数据结构,这些数据结构以某种方式引用(指向)数据,这样就可以在这些数据结构上实现高级查找算法。这种数据结构,就是索引。
为表设置索引要付出代价的:一是增加了数据库的存储空间,二是在插入和修改数据时要花费较多的时间(因为索引也要随之变动)。
上图展示了一种可能的索引方式。左边是数据表,一共有两列七条记录,最左边的是数据记录的物理地址(注意逻辑上相邻的记录在磁盘上也并不是一定物理相邻的)。为了加快 Col2 的查找,可以维护一个右边所示的二叉查找树,每个节点分别包含索引键值和一个指向对应数据记录物理地址的指针,这样就可以运用二叉查找在 O(log2n)的复杂度内获取到相应数据。
创建索引可以大大提高系统的性能。
第一,通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。
第二,可以大大加快数据的检索速度,这也是创建索引的最主要的原因。
第三,可以加速表和表之间的连接,特别是在实现数据的参考完整性方面特别有意义。
第四,在使用分组和排序子句进行数据检索时,同样可以显著减少查询中分组和排序的时间。
第五,通过使用索引,可以在查询的过程中,使用优化隐藏器,提高系统的性能。
也许会有人要问:增加索引有如此多的优点,为什么不对表中的每一个列创建一个索引呢?因为,增加索引也有许多不利的方面。
第一,创建索引和维护索引要耗费时间,这种时间随着数据量的增加而增加。
第二,索引需要占物理空间,除了数据表占数据空间之外,每一个索引还要占一定的物理空间,如果要建立聚簇索引,那么需要的空间就会更大。
第三,当对表中的数据进行增加、删除和修改的时候,索引也要动态的维护,这样就降低了数据的维护速度。
索引是建立在数据库表中的某些列的上面。在创建索引的时候,应该考虑在哪些列上可以创建索引,在哪些列上不能创建索引。一般来说,应该在这些列上创建索引:在经常需要搜索的列上,可以加快搜索的速度;在作为主键的列上,强制该列的唯一性和组织表中数据的排列结构;在经常用在连接的列上,这些列主要是一些外键,可以加快连接的速度;在经常需要根据范围进行搜索的列上创建索引,因为索引已经排序,其指定的范围是连续的;在经常需要排序的列上创建索引,因为索引已经排序,这样查询可以利用索引的排序,加快排序查询时间;在经常使用在 WHERE 子句中的列上面创建索引,加快条件的判断速度。
同样,对于有些列不应该创建索引。一般来说,不应该创建索引的的这些列具有下列特点:
第一,对于那些在查询中很少使用或者参考的列不应该创建索引。这是因为,既然这些列很少使用到,因此有索引或者无索引,并不能提高查询速度。相反,由于增加了索引,反而降低了系统的维护速度和增大了空间需求。
第二,对于那些只有很少数据值的列也不应该增加索引。这是因为,由于这些列的取值很少,例如人事表的性别列,在查询的结果中,结果集的数据行占了表中数据行的很大比例,即需要在表中搜索的数据行的比例很大。增加索引,并不能明显加快检索速度。
第三,对于那些定义为 text, image 和 bit 数据类型的列不应该增加索引。这是因为,这些列的数据量要么相当大,要么取值很少。
第四,当修改性能远远大于检索性能时,不应该创建索引。这是因为,修改性能和检索性能是互相矛盾的。当增加索引时,会提高检索性能,但是会降低修改性能。当减少索引时,会提高修改性能,降低检索性能。因此,当修改性能远远大于检索性能时,不应该创建索引。
根据数据库的功能,可以在数据库设计器中创建三种索引:唯一索引、主键索引和聚集索引。
唯一索引
唯一索引是不允许其中任何两行具有相同索引值的索引。
当现有数据中存在重复的键值时,大多数数据库不允许将新创建的唯一索引与表一起保存。数据库还可能防止添加将在表中创建重复键值的新数据。例如,如果在 employee 表中职员的姓(lname)上创建了唯一索引,则任何两个员工都不能同姓。主键索引数据库表经常有一列或列组合,其值唯一标识表中的每一行。该列称为表的主键。在数据库关系图中为表定义主键将自动创建主键索引,主键索引是唯一索引的特定类型。该索引要求主键中的每个值都唯一。当在查询中使用主键索引时,它还允许对数据的快速访问。聚集索引在聚集索引中,表中行的物理顺序与键值的逻辑(索引)顺序相同。一个表只能包含一个聚集索引。
如果某索引不是聚集索引,则表中行的物理顺序与键值的逻辑顺序不匹配。与非聚集索引相比,聚集索引通常提供更快的数据访问速度。
局部性原理与磁盘预读
由于存储介质的特性,磁盘本身存取就比主存慢很多,再加上机械运动耗费,磁盘的存取速度往往是主存的几百分分之一,因此为了提高效率,要尽量减少磁盘 I/O。为了达到这个目的,磁盘往往不是严格按需读取,而是每次都会预读,即使只需要一个字节,磁盘也会从这个位置开始,顺序向后读取一定长度的数据放入内存。这样做的理论依据是计算机科学中著名的局部性原理:当一个数据被用到时,其附近的数据也通常会马上被使用。程序运行期间所需要的数据通常比较集中。
由于磁盘顺序读取的效率很高(不需要寻道时间,只需很少的旋转时间),因此对于具有局部性的程序来说,预读可以提高 I/O 效率。
预读的长度一般为页(page)的整倍数。页是计算机管理存储器的逻辑块,硬件及操作系统往往将主存和磁盘存储区分割为连续的大小相等的块,每个存储块称为一页(在许多操作系统中,页得大小通常为 4k),主存和磁盘以页为单位交换数据。当程序要读取的数据不在主存中时,会触发一个缺页异常,此时系统会向磁盘发出读盘信号,磁盘会找到数据的起始位置并向后连续读取一页或几页载入内存中,然后异常返回,程序继续运行。
B-/+Tree 索引的性能分析
到这里终于可以分析 B-/+Tree 索引的性能了。
上文说过一般使用磁盘 I/O 次数评价索引结构的优劣。先从 B-Tree 分析,根据 B-Tree 的定义,可知检索一次最多需要访问 h 个节点。数据库系统的设计者巧妙利用了磁盘预读原理,将一个节点的大小设为等于一个页,这样每个节点只需要一次 I/O 就可以完全载入。为了达到这个目的,在实际实现 B-Tree 还需要使用如下技巧:
每次新建节点时,直接申请一个页的空间,这样就保证一个节点物理上也存储在一个页里,加之计算机存储分配都是按页对齐的,就实现了一个 node 只需一次 I/O。
B-Tree 中一次检索最多需要 h-1 次 I/O(根节点常驻内存),渐进复杂度为 O(h)=O(logdN)。一般实际应用中,出度 d 是非常大的数字,通常超过 100,因此 h 非常小(通常不超过 3)。
而红黑树这种结构,h 明显要深的多。由于逻辑上很近的节点(父子)物理上可能很远,无法利用局部性,所以红黑树的 I/O 渐进复杂度也为 O(h),效率明显比 B-Tree 差很多。
综上所述,用 B-Tree 作为索引结构效率是非常高的。
应该花时间学习 B-树和 B+ 树数据结构
=============================================================================================================
1)B 树
B 树中每个节点包含了键值和键值对于的数据对象存放地址指针,所以成功搜索一个对象可以不用到达树的叶节点。
成功搜索包括节点内搜索和沿某一路径的搜索,成功搜索时间取决于关键码所在的层次以及节点内关键码的数量。
在 B 树中查找给定关键字的方法是:首先把根结点取来,在根结点所包含的关键字 K1,…,kj 查找给定的关键字(可用顺序查找或二分查找法),若找到等于给定值的关键字,则查找成功;否则,一定可以确定要查的关键字在某个 Ki 或 Ki+1 之间,于是取 Pi 所指的下一层索引节点块继续查找,直到找到,或指针 Pi 为空时查找失败。
2)B+ 树
B+ 树非叶节点中存放的关键码并不指示数据对象的地址指针,非也节点只是索引部分。所有的叶节点在同一层上,包含了全部关键码和相应数据对象的存放地址指针,且叶节点按关键码从小到大顺序链接。如果实际数据对象按加入的顺序存储而不是按关键码次数存储的话,叶节点的索引必须是稠密索引,若实际数据存储按关键码次序存放的话,叶节点索引时稀疏索引。
B+ 树有 2 个头指针,一个是树的根节点,一个是最小关键码的叶节点。
所以 B+ 树有两种搜索方法:
一种是按叶节点自己拉起的链表顺序搜索。
一种是从根节点开始搜索,和 B 树类似,不过如果非叶节点的关键码等于给定值,搜索并不停止,而是继续沿右指针,一直查到叶节点上的关键码。所以无论搜索是否成功,都将走完树的所有层。
B+ 树中,数据对象的插入和删除仅在叶节点上进行。
这两种处理索引的数据结构的不同之处:
a,B 树中同一键值不会出现多次,并且它有可能出现在叶结点,也有可能出现在非叶结点中。而 B+ 树的键一定会出现在叶结点中,并且有可能在非叶结点中也有可能重复出现,以维持 B+ 树的平衡。
b,因为 B 树键位置不定,且在整个树结构中只出现一次,虽然可以节省存储空间,但使得在插入、删除操作复杂度明显增加。B+ 树相比来说是一种较好的折中。
c,B 树的查询效率与键在树中的位置有关,最大时间复杂度与 B+ 树相同(在叶结点的时候),最小时间复杂度为 1(在根结点的时候)。而 B+ 树的时候复杂度对某建成的树是固定的。可以扫描2的次方。
B_TREE(来源于数据结构,做个收藏)
1、B_TREE的定义
B_TREE是一种平衡多叉排序树,是一种动态查找效率很高的树形结构。B_TREE中所有结点的孩子结点的最大值称为B_TREE的阶,B_TREE的阶通常用m表示,简称为m叉树。一般来说,应该是m>=3。一颗m阶的B_TREE或是一颗空树,或者是满足下列条件的m叉树:
- 树中每个结点最多有m个孩子结点;
- 除根结点外,其它结点至少有(int)m/2+1个孩子结点;
- 若根结点不是叶子节点,则根结点至少有2个孩子结点;
- 结点的结构:
 其中,n为结点中关键字个数,(int)m/2<=n<m;di(1<=i<=n)为该结点的n个关键字值的第i个,且di<d(i+1);ci(0<=i<=n)为该结点孩子结点的指针,且ci所指向的节点的关键字均大于或等于di且小于d(i+1);
其中,n为结点中关键字个数,(int)m/2<=n<m;di(1<=i<=n)为该结点的n个关键字值的第i个,且di<d(i+1);ci(0<=i<=n)为该结点孩子结点的指针,且ci所指向的节点的关键字均大于或等于di且小于d(i+1); - 所有的叶结点都在同一层上。
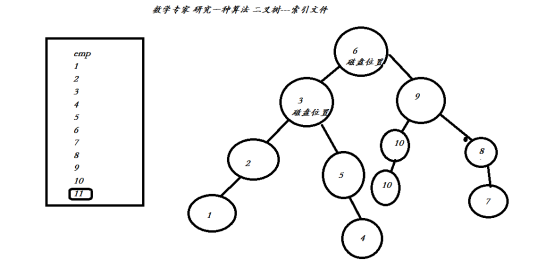
一棵4阶B_TREE的示例。4叉树结点的孩子结点的个数范围[2,4]。其中,有2个结点有4个孩子结点,有1个结点有3个孩子结点,有5个结点有2个孩子结点。

图 一棵4阶B_TREE
2、B_TREE的查找
在B_TREE上查找x,现将x的关键字与根结点的n个关键字di逐个比较,然后做如下处理:
- 若x.key==di,则查找成功返回;
- 若x.key<d1,则沿着指针c0所指的子树继续查找;
- 若di<x.key<d(i+1),则沿着指针ci所指的子树继续查找;
- 若x.key>dn,则沿着指针cn所指的子树继续查找。
3、B_TREE的插入
将元素x插入到B_TREE的过程为:
- 查找到x应该插入的结点(插入结点一定是叶结点);
- 判断该结点是否还有空位置,即判断该结点是否满足结点关键字的个数n小于m-1这个条件。若n<m-1,则说明该结点还有空位置,直接把数据插入(注意插入时要满足B_TREE结点结构定义);若n=m-1,则需要分裂该结点,即以中间关键字为界(包括要插入的关键字)把结点分为两个结点,并把中间元素向上插入到双亲结点,若双亲结点未满,则把它插入到双亲结点合适的位置,否则,继续往上分裂(直到根结点分裂可能会有树的高度增1的可能)。
4、B_TREE的删除
定义要删除结点x的关键字的个数为n,l=(int)m/2;
- 查找x是否存在,若不存在,则返回;若存在,则继续;
- 对于叶结点上的删除,分为3种情况:1、n>l则直接删除该数据元素;2、n=l且该结点左(右)兄弟结点关键字个数大于l,把删除数据元素结点的左(右)兄弟结点中最大(小)的元素上移到双亲结点上,同时把双亲结点中大于(小于)上移关键字的关键字下移到要删除数据元素的结点上;3、n=l且该结点左(右)兄弟结点关键字个数等于l,把要删除数据元素的结点的左(右)兄弟结点以及双亲结点上分割二者的数据元素合并成一个结点;
- 对于非叶结点的删除,可以转换为叶结点上的删除:假设要删除的元素为di,首先寻找要删除数据元素的结点的ci所指向子树中的最小关键字,设为d(min),然后把k(min)复制到ki,最后删除关键字为k(min)的元素(此时的k(min)必为某个叶结点上的元素)。


