测试用例设计之正交实验法

1.正交表介绍

标准正交表:

　　Ln(m^k)  :  

　　　　L: 表示正交表

　　　　n: 实验行数   且 n = (m-1)*k + 1

　　　　k: 因素数 (输入 或 控件数量)

　　　　m: 水平数 (输入的取值 或者 每个控件的下拉选项数量)

　　　　标准正交表的每个因素的水平数相同.

混合正交表:

　　Ln(m1^k1m2^k2m3^k3.......)

　　　　L: 表示正交表

　　　　n: 实验行数   且 n = (m1-1)*k1 + (m2-1)*k2+(m3-1)*k3+.........+1

　　　　m1^k1: k1个控件有m1个选项

　　　　m2^k2: k2个控件有m2个选项

　　　　m3^k3: k3个控件有m3个选项

2.正交表法应用场景:

　　多条件组合用例设计，但是不适用依赖和联动（比如省市区那样的下拉框）。常见于页面组合设置用例设计和兼容性组合用例设计。用最少的实验覆盖最多的操作，测试用例设计很少，效率高。正交性从全面试验中挑选出部分有代表性的点进行试验。

3.正交表设计步骤

设计测试用例的步骤：

1、确定因子（变量）

2、确定水平（变量的取值）

3、选择一个合适的正交表

4、把变量的值映射到表中

5、把每一行的各因素水平的组合作为一个测试用例

6、加上你认为可疑且没有在表中出现的用例组合

4.选择正交表

1、考虑因素（变量）的个数

2、考虑因素水平（变量的取值）的个数

3、考虑正交表的行数

4、取行数最少的一个

正交表查询地址

http://support.sas.com/techsup/technote/ts723_Designs.txt

5.设计用例时三种情况

因子和水平相符，且水平数（变量的取值）相同、因素数（变量）刚好符合某一正交表，则直接套用正交表，得到用例。

 

例子：

 

对某人进行查询，假设查询某个人时有三个查询条件：

 

根据“姓名”进行查询

 

根据“身份证号码”查询

 

根据“手机号码”查询

 

考虑查询条件要么不填写，要么填写，此时可用正交表进行设计

 

① 因素数和水平数

 

有三个因素：姓名、身份证号、手机号码。每个因素有两个水平：

 

姓名：填、不填

 

身份证号：填、不填

 

手机号码：填、不填

 

② 选择正交表

 

表中的因素数＞＝3

 

表中至少有三个因素的水平数＞＝2

 

行数取最少的一个

 

结果：L4(2^3)

 

 

③ 变量映射

 

姓名：1→填写，2→不填写；

 

身份证号：1→填写，2→不填写；

 

手机号码：1→填写，2→不填写；

 

④ 用L4(2^3)设计的测试用例

 

测试用例如下：

 

1：填写姓名、填写身份证号、填写手机号

 

2：填写姓名、不填身份证号、不填手机号

 

3：不填姓名、填写身份证号、不填手机号

 

4：不填姓名、不填身份证号、填写手机号

 

⑤增补测试用例

 

5：不填姓名、不填身份证号、不填手机号

 

测试用例减少数：8→5

 

因素数不相同

水平数（变量的取值）与某正交表相同，但因素数（变量）却不相同，则取因素数最接近但略大于实际值的正交表表，套用之后，最后一列因素去掉即可。

例子：

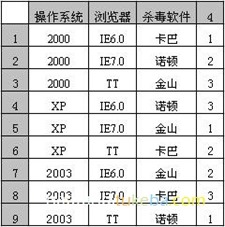
兼容性测试：

操作系统：2000、XP、2003

浏览器：IE6.0、IE7.0、TT

杀毒软件：卡巴、金山、诺顿

如果全部进行测试的话，3^3=27个组合，需要进行27次测试。

① 因素数和水平数

有三个因素：

操作系统、浏览器、杀毒软件

每个因素有三个水平。

② 选择正交表

表中的因素数＞＝3

表中至少有三个因素的水平数＞＝3

行数取最少的一个

结果：L9(3^4)，如下图：

③ 变量映射

操作系统：1→2000，2→XP，3→2003

浏览器：1→IE6.0，2→IE7.0，3→TT

杀毒软件：1→卡巴，2→金山，3→诺顿

④用L9(3^4)设计的测试用例

测试用例如下：

2000、IE6.0、卡巴

2000、IE7.0、诺顿

2000、TT、金山

XP、IE6.0、诺顿

XP、IE7.0、金山

XP、TT、卡巴

2003、IE6.0、金山

2003、IE7.0、卡巴

2003、TT、诺顿

⑤增补测试用例

由于目前IE6.0、XP、卡巴的使用量很高，故增添以下测试用例：

XP、IE6.0、金山

XP、IE6.0、卡巴

2003、IE6.0、卡巴

测试用例减少数：27→12

 

3、水平数不相同（最常见，必掌握）

因素（变量）与某正交表相同，但水平数（变量的取值）不相同。

例子：

假设有一个系统有5个独立的变量（A，B，C，D，E）。变量A和B都有两个取值（A1 、A2和B1、B2）。变量C和D都有三个可能的取值（C1、C2、C3和D1、D2、D3）。变量E有六个可能的取值（E1、E2、E3、E4、E5、E6）。

① 因素数和水平数

有五个因素（变量）：

A、B、C、D和E

两个因素有两个水平（变量的取值）、两个因素有三个水平，一个因素有六个水平：

A：A1、A2

B：B1、B2

C：C1、C2、C3

D：D1、D2、D3

E：E1、E2、E3、E4、E5、E6

② 选择正交表

表中的因素数（变量）＞＝5

表中至少有二个因素的水平数（变量的取值）＞＝2

至少有另外二个因素的水平数＞＝3

还至少有另外一个因素的水平数＞＝6

行数取最少的一个：L49(7^8)或者L18(3^6 6^1)）

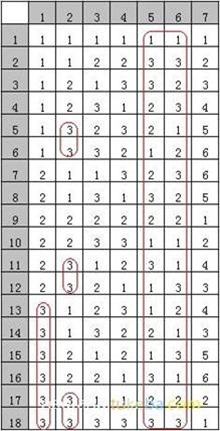
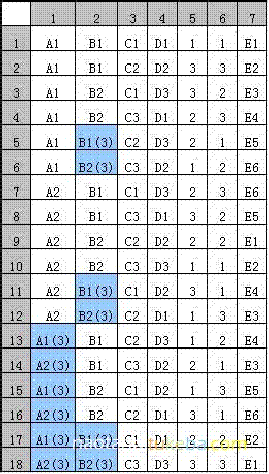
结果：L18(3^6 6^1)（如下图）

③ 变量映射

A：1→A1、2→A2

B：1→B1、2→B2

C：1→C1、2→C2、3→C3

D：1→D1、2→D2、3→D3

E1、2→E2、3→E3、4→E4、5→E5、6→E6

④ 用L18(3^6 6^1)设计的测试用例

略

测试用例减少数：216→18

加上一些可疑的情况（设为n个）为18＋n，它比原来也少多了。

6.ALLpairs工具生成混合正交表

下载地址

https://www.softpedia.com/dyn-search.php?search_term=allpairs 

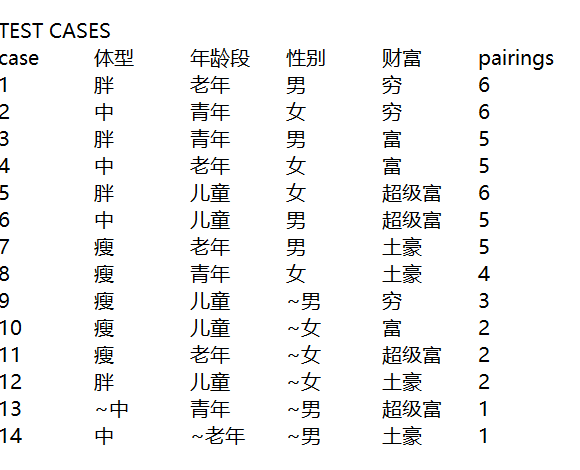
1、先根据测试要求得到取值表（下面是我一个案例取值表）用excel表

 

2、将取值表数据复制粘贴到新建的test.txt文本当中

3、将test.txt放进allpairs所解压的文件夹里面如下：

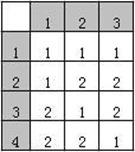
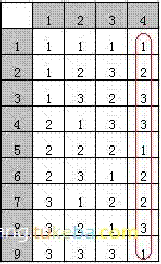
 4.在命令行执行allpairs.exe test.txt>test1.txt 

test1.txt即为所需正交表，波浪线表示可以选任一水平。