腐蚀膨胀运算是数学形态学中的基本运算。数学形态学的基础是集合论，用来表示和描述区域性状很有用。它的应用可以简化图像数据，保持它们的基本形状特性并去除不相干的结构。形态学有四个基本运算：腐蚀，膨胀，开运算和比运算。这里我们实现一种基于腐蚀膨胀运算实现的自适应对比度增强算法。
首先我们看一下腐蚀和膨胀运算，他们是应用于二值图像的。通过一个探针，也是一个集合，称为结构元素，对二值图像（也是一个集合）进行变换，以突出所需要的信息。结构元素的大小和形状会影响图像处理的结果，他们由分析的目的来确定。
腐蚀运算用来收缩或者细化对象，结构元素的大小和形状决定了收缩的程度和范围。腐蚀运算用某个结构元素对二值图像进行探测，找出图像内部可以容纳该结构元素的区域。它是一种消除边界点，是边界向内部收缩的过程。具体的数学公式不去探讨，腐蚀运算是对于二值图像的每个点，如果在结构元素范围内的所有点都为1，则该点为1。否则为0。而膨胀运算是使二值图像加长或变粗的操作。对于二值图像的每个点，在结构元素范围内的所有点如果都为0，则该点为0。否则为1。可见腐蚀和膨胀运算是对于二值图像中的亮点（值为1）而言的。腐蚀操作后，图像中的亮点范围缩减。相反，膨胀元算后，亮点的范围增大。
了解了二值图的腐蚀膨胀运算，我们就可以把腐蚀膨胀运算推广到任意的灰度图。对于任意灰度图，腐蚀运算就是求结构元素范围内（领域）最小值，即腐蚀运算使领域中心值变为为结构元素内的最小像素值。比如，结构元素为矩形领域，则腐蚀运算对每个像素求取以它为中心的矩形领域内的最小像素值。类似的，膨胀运算就是求领域最大值。
简单起见，以方形领域为结构元素。其算法和领域均值和领域中值的算法类似，可以用领域直方图更新算法来优化。下面是对灰度图像的腐蚀膨胀结果。
原图 领域半径2的亮度通道腐蚀结果 领域半径2的亮度通道膨胀结果
对于任意灰度来说，膨胀腐蚀运算就是对白色来说的。膨胀运算使得亮部增加，也就是白色的范围增大，图像中的笔画变得粗大。反之腐蚀运算使得亮部减少，白色范围缩减，笔画变得细小。
下面是对彩色图像亮度通道腐蚀膨胀运算结果。
原图 领域半径5的亮度通道腐蚀结果 领域半径5的亮度通道膨胀结果
取不同的半径可以产生不同的效果，感觉有点像油画似的。
记图像原图为I，对图像的腐蚀运算记为E(I)，膨胀运算记为D(I)。既然腐蚀运算使得亮部减少，保留了局部最暗值，那么原图像和腐蚀结果的差值
为局部亮斑的图像。同理膨胀运算使得亮部增加，保留了局部最亮值，那么
则为局部暗斑的图像。注意这里的局部二字，所谓的亮斑和暗斑都是限定在这个所谓的局部（领域）里面的。
对比度增强，简单的说就是让图像中亮的地方更亮，暗的地方更暗，拉大对比度。既然我们得到了局部亮斑P1和局部暗斑P2，那么对比度增强运算可以表示为结果图像
，a1，a2为控制系数，分别控制要增强的局部亮部和暗部的程度，使得在原图的基础上，亮的地方（P1）更亮，暗的地方（P2）更暗。
到这里，只要用户给出不同的a1，a2，就可以实现对比度增强了。但是要做到算法的自适应，a1和a2就不能是全局的一个固定的常数。那么怎么来实现a1和a2的自适应呢？我们知道，一般传统自适应对比度增强算法为了达到自适应的目的，控制参数是由局部均方差来计算的。局部均方差的大小反映了局部的像素和均值的偏离程度。均方差越大，像素偏离均值越大，说明局部原本的对比度就比较大，那么对比度增强的幅度就不需要很大。反之，均方差小，说明原本对比度小，对比度增强的幅度就要大一些。在这里，借鉴这种思想，仿照传统的用均方差来做自适应的对比度增强方法，使控制系数也能达到自适应的目的。
但是考虑到腐蚀和膨胀运算不是计算的期望值，这里不是计算对于局部均值的偏差，所以不能直接应用局部均方差。这里要计算的是对指定值（局部最大值或者最小值）的偏差，可以把要计算的均方差称作伪均方差，或者偏均方差。偏方差为
这样局部偏方差可以通过这个公式得出。其中前两项求和为领域平方和，以及领域和。这两项求和可以用积分图来计算。不过要注意平方积分图值会很大，如果领域半径很大的话，需要相应改变数据类型以避免发生溢出。如果是为a1求偏方差，则e为领域最小值。如果是为a2求偏方差，则e为领域最大值。均偏方差就是偏方差的平方根。即
Ad，Ae是输入参数，分别控制膨胀腐蚀对比度增强的数量。那么最后对比度增强的图像公式是
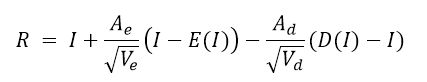
Ae实际上控制了亮部增强的数量，数值越大，图像中亮的地方越亮，我把它称作高光数量。Ad实际上控制了暗部增强的数量，这个数值越大，图像中黑的地方越黑，我把它称作暗影数量。下面是一些图片用这种对比度增强的结果。
原图 高光（腐蚀）半径200，增强幅度50，暗影（膨胀）半径75，增强幅度10
原图 高光（腐蚀）半径116，增强幅度32，暗影（膨胀）半径79，增强幅度76
可以看到效果还是不错的。相比于通常的自适应对比度增强算法，这种应用腐蚀膨胀运算的自适应对比度增强算法的最大优点是可以对图像的亮部和暗部分别控制进行对比度增强。有些图像可能整体集中于偏亮或者偏暗的部分，如果用通常的自适应对比度增强算法，它是对亮部暗部统一操作的，也就是说可以认为它对亮部和暗部的扩展是一样程度的。比如如果图像整体偏暗，可能亮部的对比度延展还没有达到需要，暗部的对比度可能就已经调整的太暗了，使很多比较暗的像素下溢出了，也就是全变成黑色了，这是我们不希望的。而使用这种应用腐蚀膨胀运算的自适应对比度增强算法，就可以控制暗部的对比度保持一个较小的扩展量，甚至不扩展（Ad为0），而亮部可以应用较大的对比度扩展量，从而达到我们的要求。下图是对一幅图像分别应用传统的自适应对比度增强算法和应用膨胀腐蚀的自适应对比度增强算法的比较。
原图 传统自适应对比度增强半径100，增强幅度50
原图整体比较偏暗，使用传统的自适应对比度增强，亮部和暗部扩展量是一样的。当对比度增强幅度为50的时候，原来图像中较暗的部分很多已经产生或者接近下溢出了，暗部的细节根本就已经分辨不出来了。
高光（腐蚀）半径100，增强幅度50，暗影（膨胀）半径150，增强幅度10 高光（腐蚀）半径100，增强幅度90，暗影（膨胀）半径150，增强幅度10
而采用基于膨胀腐蚀的局部自适应对比度增强，保持高光增强幅度50不变的情况下，减少暗影增强幅度，完全减少了暗像素下溢出的可能，整体表现情况要好很多。在亮部调整还有很多余量的情况下，保持暗部对比度增强不变，还可以根据需要继续提高亮部的对比度幅度。
分享一个实现这种基于膨胀腐蚀的局部自适应对比度增强算法的windows程序，可以看看效果。
