在一种基于腐蚀膨胀运算实现的局部自适应对比度增强算法中,提出了一种可以分开自适应的调整局部亮部和暗部对比度的方法。但是就象在评论中提到的,这种方法会产生方块效应。特别是在对比度已经比较大的边缘附近,这种方块效应会比较明显。这是因为在边缘附近,对比度本来就是比较大的,偏均方差也就相应的比较大。那么调整的时候给出自适应的调整量就会相应地变小。一旦离开边缘附近,领域不包括边缘,对比度就会相对陡然变小,那么自适应的调整量就会相应变大。那么在边缘同一侧就可能会比较明显地出现不均匀的变化,也就是我们所说的方块效应。不均匀变化的位置离边缘的位置之间的距离就是所使用的高光半径或者暗影半径大小。
看一下示例。这里为了明显显示方块效应,选择了一张前景和背景反差比较大的图片。同时这里我特意把高光半径和暗影半径选的不一样,这样我们就可以看到在不同半径的地方有两个明显的不均匀变化。


原始图片(1024x701) 高光半径100,高光数量30,暗影半径50,暗影数量30,产生方块效应
消除方块效应的办法,一个是在做完对比度调整后,再做一个高斯模糊之类的低通滤波平滑这种不均匀。这种方法不可避免地会减小图像整体清晰度。另一个简单的应对方法是,扩大所使用的领域。领域越大,包含像素越多,那么移动领域时对比度变化幅度就不会特别剧烈(即使在边缘附近),这样使得调整量的变化幅度也会大幅减少,极大地减少了方块效应。但同时,领域的扩大,也使得不同像素的领域不管是腐蚀还是膨胀结果都更加趋同,失去了所谓的局部自适应的效果。极限情况我们想象一下,如果领域半径接近甚至超过图像大小,那么所有像素的腐蚀或者膨胀结果都是一样的了。那么自适应调整量也就都一样了,那就是一个全局的调整量了。
那么有没有一种方法既能减小方块效应,又避免这些副作用呢?方块效应产生的根源是在图像边缘附近对比度的变化过大导致的。那是否能过滤这种变化呢?这让我想到了有保边效果的选择性平滑所使用的方法。比如选择性均值平滑,不是把领域内的所有像素一起求平均值,而是选择领域内和中心像素的差值小于一定阈值的所有像素求平均值。假设在领域内有一个边缘,如果设定合适的阈值,就能把和中心像素在边缘另一侧的像素都排除掉,只使用和中心像素同侧的像素参与计算,结果既保留了边缘,也起到了平滑效果。如果应用这种思想,在计算自适应调整量时,具体就是在计算膨胀或腐蚀结果的偏方差的时候,只选择和膨胀或腐蚀结果像素差值小于一定阈值的像素参与计算偏方差,理论上应该就能消除方块效应了。
原理上来说和原始方法没有大的区别,就是需要多设置一个阈值
- 膨胀腐蚀计算时也是选择性的,选择领域内和中心像素差值小于阈值的所有像素中的最大值(膨胀)和最小值(腐蚀)。
- 计算偏方差也是选择性的,选择领域内和中心像素差值小于阈值的所有像素参与计算。公式是一样的,只是求和不是所有像素总数n。

剩下的其他步骤都是一样的。
如何计算选择性膨胀腐蚀,还有选择性偏方差的方法也是一个问题。其中需要计算领域极值,均值和平方均值。原始算法是用积分图来计算领域平方和和领域和,现在选择性求和,积分图不再适用了。在选择性平滑方法中经常使用的是O(1)复杂度的领域直方图更新算法,原始论文可以在Median Filtering in Constant Time找到。我们在这里也可以用它,它的计算量基本和领域半径无关。而且使用领域直方图更新算法,可以计算多种选择性领域值,比如平均值,中值,极值,平方和均值,还可以应用表面模糊算法,局部直方图均衡等等。领域直方图更新算法的主要思想是,计算领域内所有像素直方图。当我们从左到右,从上到下移动时,每次移动更新一次领域直方图。更新时减去移出领域的所有像素的直方图,加上新进入领域的所有像素的直方图,这只需要较少的计算量。具体的为加快计算,还保持更新和领域高度相同的所有列的直方图,这样更新领域直方图时,只需加减相应的列直方图即可。具体算法这里不多做讨论了。
有了领域直方图,就可以很简单地计算选择性平均值和平方和均值。如下代码计算选择性均值。选择性平方和均值,还有极值也很简单。

{
/* int cen: 中心像素
* int threshold: 阈值
* Hist[]: 领域直方图
*/
int l;
unsigned long weight = 0, sum = 0;
int low, high;
low = cen - threshold;
if (low < 0) low = 0;
high = cen + threshold;
if (high > 255) high = 255;
for (l = low; l <= high; l++)
{
sum += Hist[l] * l;
weight += Hist[l];
}
return sum / weight;
}
对于高光调整计算,一次直方图更新算法可以得到选择性平方和均值,均值和最小值。再做一次直方图更新算法可以得到暗影调整所需的值。如果高光和暗影半径是一样的话,只需要一次直方图更新算法就可以得到高光暗影调整所有需要的结果。再遍历一次图像,应用到所有像素即可。
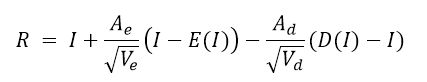
看一下效果。无阈值相当于领域内所有像素都参与计算,如前所述会产生方块效应。保持高光和暗影半径不变,随着阈值减小,方块效应也会减小,达到我们希望的结果了。


原始图片(1024x701) 高光半径100,高光数量30,暗影半径50,暗影数量30,无阈值


高光半径100,高光数量30,暗影半径50,暗影数量30,阈值50 高光半径100,高光数量30,暗影半径50,暗影数量30,阈值10
分享一个测试程序https://files.cnblogs.com/files/mightycode/edcontrast.7z,需要安装vc++ 2015-2019 redistributable。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号