【问题】
现在有一种彩票,总的有N个选择(比如36选7,那么总的选择就是36种),请问期望用多少次可以取到所有的彩票(有放回--当然,没放回就简单了。。。)?
同样的一个题目就是:一个袋子里放N个不同的球,有放回的取球。请问期望用多少次可以取到所有不同的球?
【解答】
粗略的答案,这个期望次数是随着N的规模成O(N*logN)的规模扩大的。
下面是分析:我们采取递推的方式,假设现在已经取到了i-1个不同的球或者不同的彩票(我们下边都用球代替),那么下一次取到第i个球的概率是:
( N - ( i - 1 ) ) / N
这个很显然:下次想取到一个跟以前的球不同的球,显然是在剩下的N-(i-1)个球中任取一个,概率就是除以总的球数。由于这个事件符合几何分布,所以其期望就是1/p。
我们用E(Xi)表示取到第i个球这个事件的期望的次数,那么总的取到所有的N个球的数学期望E(X)就是从E(X0),E(X1)......加到E(XN)。如下图所示(这里面的T就是我所说的X):

也就是说这个数最后就等于n乘以调和级数。(调和级数就是从1/1加1/2,一直加到1/n,也就是公式中的Hn,harmonic progression)。而调和级数是有公式可求的,所以最后结果就是:
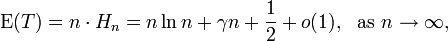
所以基本上这个答案是按照N*ln N增长的。
【参考文献】




