所谓子集,是一个数学中的概念。例如一个集合S = {1,2,3,4,5},那么X = {1,3,5}就是它的一个子集,1+3+5等于9就是对应于X的一个子集和。其实子集对于一个数组来说,就是相当于一个子序列(不是子数组,因为子序列意味着可以不连续,而子数组往往是连续的);那么子集和也就是子序列和。
另外,子集问题需要与数学中的“排列”问题区分开来。因为子集往往是无序的,但排列是需要考虑顺序的;所以子集问题常常只是一个“组合”问题,而不是“排列”问题。
从另一个角度讲,这种子集和问题是一种背包问题的特例。
【问题1】
下面举一个退化(之所以说退化,因为这里的子集的大小是2,比较特殊)的子集和问题的例子,出自《编程之美》P.178的问题:快速寻找满足条件的两个数。
问题如下:给定一个数M,在数组arr中寻找两个数,使得这两个数之和等于M。
最初的想法就是:把数组中任意两个数的和求出来(复杂度是N^2),然后在这个和的数组中遍历,查找是否存在等于M的数。
但是这个问题还有更巧妙的方法,采用“变治”:将问题转化为另一个问题再求解。第一种变治方法就是将求两个数的和,转化为是否能在数组中找到M减去数组任意元素的差。但是这种方案没有降低任何复杂度。于是想到了第二种“变治”方法:对数组进行预处理排序,然后从数组的两头用两个指针开始向中间搜索(如果两个指针所指的和小于M,则左指针右移;反之则右指针左移)。
【问题2】
还是《编程之美》中的“数组分割”问题,详见P207。
【问题3】
输出一个集合的所有子集,也就是一个集合的所有组合(你想到了什么?)。
也有递归的解法,这里的递归思想就是:
f(判断第i个数)
{
若n个数都判断完(i>=n),输出刚才所取的数,返回。
否则:
不取第i个数,
f(判断第i+1个数)
取第i个数,
f(判断第i+1个数)
}
代码如下:
#include <vector>
using namespace std;
void all_subset( int arr[], unsigned int size, vector<bool>& contains, int depth )
{
//when reach the needed length, output
if ( depth == size )
{
for( int j = 0 ; j < size ; j++ )
{
if( contains[j] )
cout<<arr[j]<<" ";
}
cout<<endl;
}
else
{
// generate the result that doesn't contain arr[depth]
contains[depth] = false;
all_subset( arr, size, contains, depth+1 );
// generate the result that contains arr[depth]
contains[depth] = true;
all_subset( arr, size, contains, depth+1 );
}
return;
}
int main()
{
int s[] = { 1, 2, 3, 4, 5 };
int size = sizeof(s)/sizeof(int);
vector<bool> contains( 5, false );
all_subset( s, 5, contains, 0 );
}
用形象的“状态空间树”来表示上面的过程,如下:
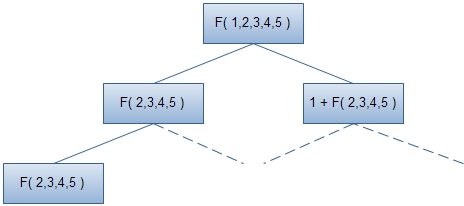
我们假设对于一个集合生成所有子集的函数为F。那么F(1,2,3,4,5)将由两种可能组成:(1)对除1之外的元素组成的集合施加F;(2)对必然包含1在内的所有元素组成的集合施加F。注意:这两种情况是互斥的,所以不可能有情况重复!然后继续递归下去,就能生成最后结果。
===============================
当然这个问题也有另外一种解法:我们知道一个集合的子集的个数就等于其所有组合之和,即任选1个元素的集合个数+任选2个元素的集合个数+任选3个元素的集合个数+......+任选N个元素的集合个数,最后结果呢是2的N次方个。既然是2的N次方,我们就可以用二进制位表示,如果某位为1,则表示这个集合中含有这一位所代表的元素。例如一个集合是{1,2,3,4,5},则二进制10011就表示这个集合为{1,4,5}。这个代码我就不写了,然后将这个数每次加1,只要判断某位是否为1即可。
【问题4】
子集和问题。题目如下:
在X中寻找子集Yi,使得Yi中元素之和等于y。
下面是回溯法的代码:
#include <vector>
#include <algorithm>
#include <string>
using namespace std;
//find if the given subset sum exists.
int findSubsetSum( vector<int>& arr, int given, vector<bool>& included )
{
int cur = 0; // 指向当前值.
int sum = 0; // 当前子集合和.
while( cur >= 0 )
{
//if current one is not included
if( false == included[cur])
{
//include current one
included[cur] = true;
sum += arr[cur];
//find the given subset sum
if( sum == given )
{
return 1;
}
else if( sum > given ) //exceed the given sum
{
included[cur] = false;
sum -= arr[cur];
}
cur++;
}
//backtrace
if( cur >= arr.size() )
{
/*
** 下面两个循环依次排除匹配不成功的结果中
** 包括在结果内以及不包括在结果内的元素
** 直到找到下一个包括在结果内的元素
** 例如:用1和0表示包括和未包括
** 若结果为1110011,则第三个1为所找元素
** 将其变为0,但是从第4个0开始遍历。
**/
while( true == included[cur-1] )
{
cur--;
included[cur] = false;
sum -= arr[cur];
//backtrace to the head
if(cur < 1)
return 0;
}
while( false == included[cur-1] )
{
cur--;
if( cur < 1 )
return 0;
}
//change the status of current - 1,not current!
included[cur-1] = false;
sum -= arr[cur-1];
}
}
return 0;
}
int main()
{
int arr[] = { 2,5,15,8,20 };
vector<int> v( arr, arr + sizeof(arr)/sizeof(int) );
vector<bool> included( sizeof(arr)/sizeof(int), false );
int given = 33;//5+8+20
if( findSubsetSum( v, given, included ) )
{
vector<bool>::iterator iterb = included.begin();
vector<int>::iterator iteri = v.begin();
for( ; iterb != included.end() ; iterb++,iteri++ )
{
if( *iterb )
cout<<*iteri<<endl;
}
}
}
这个问题还有动态规划的方法,以后补充上。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号