【问题】
原文参见这里:http://yueweitang.org/blog/posts/rotate-coin-games.html
原文中只给出了一个结果,但是没有分析过程。最后我逆向了一下,有点拾人牙慧。
我再引用一下人家的题目:
游戏轮流进行直到棋盘上所有硬币都正面朝上或者反面朝上,Alice获得胜利。
如果Alice在游戏过程中无法看到棋盘上的银币,也不知道游戏刚开始的状态,甚至不知道Bob每回合是否旋转了棋盘,那么Alice有策略能够获得胜利么?他的最优策略是什么?
【思考】
这个问题是个非常好的锻炼思维的题目。但根据葡萄同志顽强拼搏的意志( ),终于在睡觉之前把这个问题的思路整理如下:
),终于在睡觉之前把这个问题的思路整理如下:
(1)这是个分情况讨论,自底向上的问题。一个题目如果一上来没什么思路,那肯定就是举例子+分情况。4个硬币,需要处理的显然就是3种情况(4个全向上和4个全向下不需要处理):2个向上+2个向下;1个向上+3个向下;3个向上+1个向下。很容易看出这个其实就是两种情况:偶数个向上+偶数个向下;奇数个向上+奇数个向下。
(2)然后看进行的操作对这些情况产生的影响。当然我们得列举我们可以进行哪些操作,这算是一个难点了。我第一次卡就卡在这个地方,想象能力不够。可以进行的操作其实就是三种:对角线翻转(将对角线上的两个硬币翻转);边翻转(将一个边上的两个硬币翻转);单个硬币的翻转。
然后看看这些操作都对硬币产生了什么影响。由于题目要求4个硬币全向上或者全向下都可以,所以不用关心最终状态的反正,我们只需要关心硬币状态是否一致就可以了。那么可以大致得到这样的结论:对角线翻转和边翻转都不改变整个状态的奇偶性;单个硬币翻转则改变整个状态的奇偶性。这里的奇偶性指的是:4个硬币中如果奇数个向上奇数个向下,整个状态就是奇的;如果偶数个向上偶数个向下,整个状态就是偶的。
(3)关于必胜策略。我一开始对于必胜策略的想法也错了,认为是必须执行完必胜策略的所有步骤,看最终状态。其实并不是这样,只要沿着必胜策略走,那么走到任何一步胜利都可以退出。
(4)最重要的一点,也是题目最迷惑的一点就是还存在一个干扰,就是有人可以旋转硬币的位置。其实这个干扰对于一个4个硬币的正方形来说,形同虚设。
下面的讨论都是在任意旋转的情况下进行的。你可以将我所说的操作加于任何一个对角线或者边或者硬币,都不影响最后结果。
下面用图示说明这个问题:
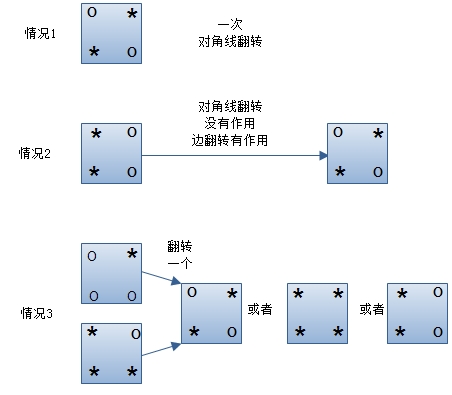
先说偶数的情况。情况1和情况2都属于偶数的情况。情况1其实不用解释了,任意的一次对角线翻转就可以搞定。情况2需要解释一下:对角线翻转对于情况2是一点作用没有,因为,对角线翻转之后,两个同样的硬币还是会在一边;但是边翻转操作就对它有用了,施加一次就可以变成情况1。于是,这两种情况最多用三步就可以解决了:一次对角线翻转(此时情况1的就胜利了)+一次边翻转+一次对角线翻转(此时情况2胜利)。
再看情况3,即奇数的情况。情况3有两种,但是殊途同归。当然,我们已经将上面的三步(对付情况1和情况2的)施加在它们身上,但是其实一点用都没有,它们还是会是这个样子。为什么呢?因为上面说过了:边翻转操作和对角线翻转操作不改变奇偶性!所以进行三次操作之后,情况3的硬币还是会保留情况3中最左端的两种状态。但是怎么能让他们改变一点呢?就剩最后一种能改变奇偶性的操作了:翻转一枚硬币。那么马上情况3就演变成了情况1和情况2,或者就直接成功退出了!之后再进行情况1和情况2中的三步操作就一定会成功了。
所以最后最多也只需要7步操作!
【参考文献】
这里还给出了当不只有4个硬币,推广到N的情况。。。
http://yueweitang.org/blog/posts/rotate-coin-game-solution.html




