数据结构之二叉树（2）二叉树遍历

本栏目是自己在学习代码随想录二叉树做的总结，部分内容来自网站 https://programmercarl.com/ （代码随想录）

2 二叉树遍历

2.1 深度优先遍历 DFS

深度优先遍历是指先朝一个方向遍历，然后回头遍历另一个方向，深度优先遍历分为前序遍历，中序遍历和后序遍历，其区别：

遍历方式	遍历方向	解释
前序遍历	中左右	先遍历中节点，再遍历左然后右
中序遍历	左中右	先遍历左节点，再遍历中然后右
后序遍历	左右中	先遍历左节点，再遍历右然后中

可以看出，区分哪种遍历方式，从字面上来看就是中的位置，一个具体的例子

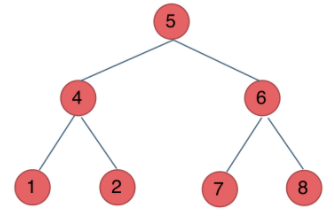
前序遍历：中左右 5412678
中序遍历：左中右 1425768
后续遍历：左右中 1247865

2.2 深度优先遍历代码实现

2.2.1 递归实现

递归实现是一个简便的方式，3种遍历的区别仅仅是读取当前节点的代码位置

这道题是leetcode的第144题，只要把放入vector的代码改变位置就能改变遍历的顺序，这里为什么要重新写一个递归函数而不在之前的函数里直接递归呢？原因是，由于要遍历整棵树，因此我们不能在遇到空节点的时候就返回值，而是要在全部遍历完后才能得到返回值，所以重新写一个递归函数，直接返回空即可。
根据代码回想录网站里的描述，当我们在满足条件即返回时就需要递归函数返回值，反之，当我们需要遍历整棵树时就不需要返回值，但需要改变树的结构时即使满足条件就返回依然需要返回值，但此时我们使用一个变量接收该返回值而不是直接return。

class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        traversal(root);
        return ret;
    }
private:
    vector<int> ret;
    void traversal(TreeNode *node) {
        if (node == nullptr) return;

        ret.push_back(node->val);      // 前序遍历
        traversal(node->left);
        // ret.push_back(node->val);   // 中序遍历
        traversal(node->right);
        // ret.push_back(node->val);   // 后序遍历
    }
};

2.2.2 迭代法实现遍历

递归实际就是一个压栈和出栈的过程，因此可以使用栈来模拟这一过程
首先把右节点压栈，在把左节点压栈，这样出栈的时候就是先出左节点，此时处理的节点也是下一棵树的中间节点。
只要把获得的数组反转一下就能得到后序遍历了，中序遍历有所不同。

class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        vector<int> ret;
        if (root == nullptr) return ret;
        stack<TreeNode*> nodeStack;
        nodeStack.push(root);
        while (!nodeStack.empty()) {
            auto currNode = nodeStack.top();
            nodeStack.pop(); // 出栈
            ret.push_back(currNode->val); // 当前节点，中

            if (currNode->right != nullptr) nodeStack.push(currNode->right);    // 右
            if(currNode->left != nullptr) nodeStack.push(currNode->left);       // 左
        }
        return ret;
    }
};

中序遍历代码实现

上面说了，中序代码与前序/后序略有不同，原因是，前序时直接处理的节点就是中间节点，而中序遍历要先处理左节点，因此修改代码如下：

class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> ret;
        stack<TreeNode*> nodeStack;
        auto currNode = root;
        while (currNode != nullptr || !nodeStack.empty()) {
            if (currNode != nullptr) {
                nodeStack.push(currNode);
                currNode = currNode->left;
            } else {
                currNode = nodeStack.top();
                nodeStack.pop();
                ret.push_back(currNode->val);   // 左节点
                currNode = currNode->right;     // 右节点
            }
        }

        return ret;
    }
};

2.3 层序遍历

层序遍历实际就是广度优先遍历，不同于深度优先遍历，层序遍历只有一种遍历方式，即从左往右逐层遍历，代码使用队列的思想

class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        vector<vector<int>> ret;
        if (root == nullptr) return ret;
        queue<TreeNode*> nodeQueue;
        nodeQueue.push(root);  // 先把根节点放入
        while (!nodeQueue.empty()) {
            vector<int> path;
            for (int i = nodeQueue.size(); i > 0; --i) { // 此处不能使用nodeQueue.size()作为条件，因为会改变
                auto currNode = nodeQueue.front();
                nodeQueue.pop();
                path.push_back(currNode->val);
                if (currNode->left) nodeQueue.push(currNode->left);
                if (currNode->right) nodeQueue.push(currNode->right);
            }
            ret.push_back(path);
        }
        return ret;
    }
};