图论相关

CHANGE LOG

2023.6.3 合并 Tarjan 算法指北与最短路与生成树算法两篇博客并略作删改，更名为 初级图论。
2023.6.4 调整最短路部分文章结构与内容，合并拓扑排序 - TopoSort 至此博客，更名为 图论相关。
2023.7.1 调整可折叠部分名称与内容，删改 Dijkstra 部分内容。

0. 写在前面

本来是 拓扑排序 - TopoSort，Tarjan 算法指北 和 最短路与生成树算法 三篇博客的，结果之后又学习了更多的图论内容，就干脆放到一起了。

考虑到笔者竞赛的生命周期本来就很短，而且也刚刚入门，写不到 q 神（指 qAlex_Weiq 的神犇博客）那种水平，是不想写博客的……但是不写自己都不会，所以还是写一写吧，给后人留点遗产~~（虽然没人会看的）~~，给自己留点回忆~~（虽然自己也不一定会再看的）~~。

~~而且万一以后有闲心了重构了呢。~~

最短路部分的代码还是 3 月的，奇丑无比，大家见谅……

1. 基本概念

emmm……写的比较抽象，都是比较形式化的东西，实际上大概理解就好。

图：一个二元组 $G=(V(G),E(G))$。其中 $V(G)$ 是非空集，称为点集，对于 $V$ 中的每个元素，我们称其为顶点或节点，简称点；$E(G)$ 为 $V(G)$ 各结点之间边的集合，称为边集。

常用 $G=(V,E)$ 表示图。
无向图：$E$ 中的每个元素为一个无序二元组 $(u,v)$，称作 无向边，简称边，其中$u,v \in V $。设 $e=(u,v)$，则 $u$ 和 $v$ 称为 $e$ 的端点。
有向图：$E$ 中的每一个元素为一个有序二元组 $(u,v)$，有时也写作 $u \to v$，称作 有向边 或弧，在不引起混淆的情况下也可以称作边。设 $e=u \to v$，则此时 $u$ 称为 $e$ 的起点，$v$ 称为 $e$ 的终点，起点和终点也称为 $e$ 的端点。并称 $u$ 是 $v$ 的直接前驱，$v$ 是 $u$ 的直接后继。
子图：对一张图 $G=(V,E)$，若存在另一张图 $H=(V',E')$ 满足 $V' \subseteq V$ 且 $E' \subseteq E$，则称 $H$ 是 $G$ 的子图，记作 $H \subseteq G$。

1.1 无向图

连通：对于一张无向图 $G=(V,E)$，对于 $u,v \in V$，若存在一条途径使得 $v_0=u,v_k=v$，则称 $u$ 和 $v$ 是 连通的。由定义，任意一个顶点和自身连通，任意一条边的两个端点连通。
连通图：若无向图 $G=(V,E)$，满足其中任意两个顶点均连通，则称 $G$ 是 连通图，$G$ 的这一性质称作 连通性。
连通分量：若 $H$ 是 $G$ 的一个连通子图，且不存在 $F$ 满足 $H \varsubsetneq F \subseteq G$ 且 $F$ 为连通图，则 $H$ 是 $G$ 的一个 连通块/连通分量 （极大连通子图）。
点割集：对于连通图 $G=(V,E)$，若 $V' \in V$ 且 $G \left[ V\backslash V' \right]$（即从 $G$ 中删去 $V'$ 中的点）不是连通图，则 $V'$ 是图 $G$ 的一个 点割集。
割点：大小为一的点割集被称作割点。
边割集：对于连通图 $G=(V,E)$，若 $E' \in E$ 且 $G=\left( V,E\backslash E' \right)$（即从 $G$ 中删去 $E'$ 中的边）不是连通图，则 $E'$ 是图 $G$ 的一个 边割集。
桥：大小为一的边割集又被称作桥。
$k$-点连通：对于连通图 $G=(V,E)$ 和整数 $k$，若 $\left| V \right|\ge k+1$ 且 $G$ 不存在大小为 $k-1$ 的点割集，则称图 $G$ 是 $k$- 点连通的，而使得上式成立的最大的 $k$ 被称作图 $G$ 的 点连通度，记作 $\kappa(G)$。（对于非完全图，点连通度即为最小点割集的大小，而完全图 $K_n$ 的点连通度为 $n-1$。）
点双连通：几乎与 $2$- 点连通完全一致，除了一条边连接两个点构成的图，它是点双连通的，但不是 $2$- 点连通的。换句话说，没有割点的连通图是点双连通的。
$k$-边连通：对于连通图 $G=(V,E)$ 和整数 $k$，若$G$ 不存在大小为 $k-1$ 的边割集，则称图 $G$ 是 $k$- 边连通的，而使得上式成立的最大的 $k$ 被称作图 $G$ 的 边连通度，记作 $\lambda(G)$。（对于任何图，边连通度即为最小边割集的大小。）
边双连通：与 $2$- 边连通完全一致。换句话说，没有桥的连通图是边双连通的。
v-DCC 和 e-DCC：与连通分量类似，也有 点双连通分量 (v-DCC)（极大点双连通子图）和 边双连通分量 (e-DCC)（极大边双连通子图）。

1.2 有向图

有向无环图：边有向，无环，AKA DAG。
可达：对于一张有向图 $G=(V,E)$，对于 $u,v \in V$，若存在一条途径使得 $v_0=u,v_k=v$，则称 $u$ 可达 $v$。由定义，任意一个顶点可达自身，任意一条边的起点可达终点。（无向图中的连通也可以视作双向可达。）
强连通：若一张有向图的节点两两互相可达，则称这张图是 强连通的。
弱连通：若一张有向图的边替换为无向边后可以得到一张连通图，则称原来这张有向图是 弱连通的。
强/弱连通分量：与连通分量类似，也有 弱连通分量 （极大弱连通子图）和 强连通分量 （极大强连通子图）。

这里想 极大性 做一个解释（非官方）：对于无向图 $G=(V,E)$ 的子图 $H$ ，若所有符合条件的节点都在 $H$ 中，不可以再添加任何点，我们就说该子图 $H$ 是 极大的。各种 连通分量 都具有 极大性。

2. 拓扑排序 - TopoSort

2.1 引入

wcy 终于考上了心仪的大学，开启了精彩的大学生活！然而光是选课这一件事就把他难住了，因为一些课程包含先修课程：

课程编号	课程名称	先修课程
C1	高等数学	无
C2	程序设计基础	无
C3	离散数学	C1,C2
C4	数据结构	C2,C3
C5	算法语言	C2
C6	编译技术	C4,C5
C7	操作系统	C4,C9
C8	普通物理	C1
C9	计算机原理	C8

wcy 想排出一个顺序，让他可以丝滑地上完这九科课，那么这个顺序应该怎么排呢？

2.2 概念

2.2.1 AOV 网

用节点表示活动，用弧表示活动之间的优先关系的有向图，叫做 AOV 网，即 Activity On Vertex Network。

比如前言中给到的这个课程表，我们可以以图的形式把他画出来：

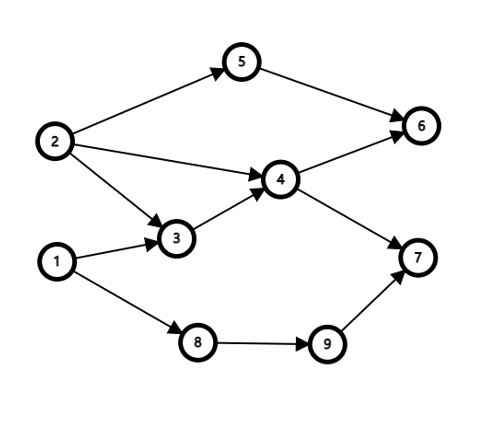
先修课程图

这就是一个 AOV 网。

2.2.2 定义与作用

拓扑排序指将 AOV 网中的节点排成一个线性序列，该序列必须满足：若从节点 $i$ 到节点 $j$ 有一条路径，则在该序列中节点 $i$ 一定在节点 $j$ 之前。

不难发现，如果一个 AOV 网有环，就必然无法得到这个 AOV 网的拓扑排序，因为他必然出现自己是自己前驱的情况。

所以，对有向图的节点进行拓扑排序后，如果所有节点都在拓扑序列中，那么就可以说明这个 AOV 网必然无环。

该 AOV 网是无环有向图 $\iff$ 该 AOV 网可进行拓扑排序

我们可以利用拓扑排序的性质 判断一个有向图为 DAG 或 创造一个线性遍历有向图的顺序，后者在树上差分，博弈论等众多图论有关内容中至关重要。

2.2.3 不唯一性

或者其实还有其他的拓扑序列：

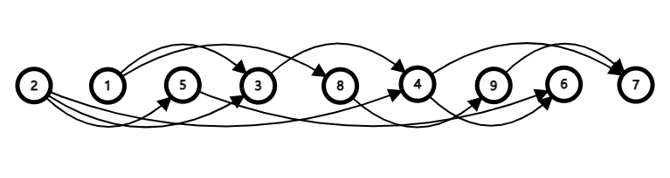
所以可见，一个AOV网的拓扑序列是不唯一的。

2.3 实践

2.3.1 基础实现

大致分为两步走：

找入度为0的点
将该点纳入拓扑序列，在图中删除该点和该点的所有边

重复这个操作。

其间，我们可能需要一个中间容器储存所有入度为零且尚未纳入序列的点。这个容器依使用情况而定，栈、队列、优先队列均可。（甚至有时候可以不需要中间容器，每次处理时都搜一次点，甚至可以通过用 DFS 辅助等方法排序，用好有奇效哦）

以栈为例的代码附上：

#include<bits/stdc++.h>
using namespace std;
int n,m,topo[MAXN],indegree[MAXN];
bool edge[MAXN][MAXN];
stack<int> s;
void TopoSort()
{
	int cnt=0;
	for(int i=1;i<=n;++i)
	{
		if(indegree[i]==0)
		s.push(i);
	}
	while(!s.empty())
	{
		int u=s.top();
		s.pop();
		topo[++cnt]=u;
		for(int j=1;j<=n;++j)
			if(edge[u][j])
				if(--indegree[j]==0)
					s.push(j);
	}
}
int main()
{
	scanf("%d%d",&n,&m);
	memset(edge,0,sizeof(edge));
	memset(indegree,0,sizeof(indegree));
	for(int i=1;i<=m;++i)
	{
		int u,v;
		scanf("%d%d",&u,&v);
		edge[u][v]=1;
		indegree[v]++;
	}
	TopoSort();
	for(int i=1;i<=n;++i)
		printf("%d ",topo[i]);
	return 0;
}

将前言中的例子送进来，就可以得到他的一个拓扑序列如图：

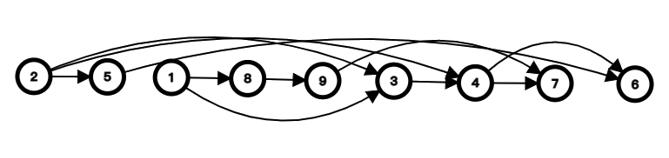
这样拓扑序列的特点就一目了然了。图中所有的箭头方向向后。

2.3.2 其他方式

其实拓扑的实现方式还是很自由的，所以我们还可以通过其他方法来实现 toposort.

比如使用搜索的写法——dfs：

#include<bits/stdc++.h>
using namespace std;
int n,m,indegree[MAXN],topo[MAXN];
stack<int>s;
vector<int>edge[MAXN];
bool dfs(int dep)
{
	if(dep>n)	return 1;
	if(dep==1)
		for(int i=1;i<=n;++i)
			if(!indegree[i])
				s.push(i);
	if(s.empty())	return 0;
	int u=s.top();
	s.pop();
	indegree[u]=-1;
	topo[dep]=u;
	for(int i=0;i<edge[u].size();++i)
		if(--indegree[edge[u][i]]==0)
			s.push(edge[u][i]);
	return dfs(dep+1);
}
int main()
{
	scanf("%d%d",&n,&m);
	for(int i=1;i<=m;++i)
	{
		int u,v;
		scanf("%d%d",&u,&v);
		edge[u].push_back(v);
		indegree[v]++;
	}
	if(dfs(1))
		for(int i=1;i<=n;++i)
			printf("%d ",topo[i]);
	else
		printf("Impossible.");
	return 0;
}

当然，你甚至可以每次搜一遍入度，抛弃中间容器，这里就展示一种：

bool dfs(int dep)
{
	if(dep>n)	return 1;
	int temp=-1;
	for(int i=1;i<=n;++i)
		if(!indegree[i])	{temp=i;	break;}
	if(temp==-1)	return 0;
	indegree[temp]=-1;
	topo[dep]=temp;
	for(int i=0;i<edge[temp].size();++i)
		indegree[edge[temp][i]]--;
	return dfs(dep+1);
}

2.3.3 判断重边

对于邻接矩阵的存图方法，由于采用布尔值存图，重边会导致入度增加而邻接矩阵不变，必然出事。所以邻接矩阵请务必判重边。

if(!edge[u][v])
{
	edge[u][v]=1;
	indegree[v]++;
}

而邻接表，如 std::vector 存图则不需要判重，这是因为我们使用 std::vector 存图通常是存该点的子节点，所以在出现重边时该子节点在入度数组和 std::vector 中都会被记录两次，也就不会出现这个问题了。 （std::vector 存图见上面 dfs 写法）

2.4 练习

2.4.1 模板题

Genealogical tree

一道非常简单的板子题

2.4.2 换个方式存图

[HNOI2015]菜肴制作

反向建边，std::vector 存图，优先队列作容器，细节拉满。

2.4.3 抓住 Toposort 的特点

排序

这道题把握拓扑排序的核心步骤：检查入度为0的点。另外需要多测进行topo。

2.4.4 Topo 全排列

Following Orders

Topo + DFS 可以想一下当初写全排列怎么写的

2.4.5 拓上 DP（doge）

旅行计划

又是你们喜欢的DP哈哈哈哈哈

2.4.6 绕个小弯

Labeling Balls

需要变通一下，非常有意思的一道题

2.4.7 CCF 荣誉出品「君のNOIP」

[NOIP2020] 排水系统

果然是 NOIP 的题，，，就非常的离谱啊，他甚至卡 ull。所以现在面前的就只有四个选择了：

高精度
使用 64 位 GCCG++ 的 _int128
其实有一种方法，由于题中提到 $d[i]≤5$ ，所以 其实所有出现的分数的分母都有且只有 2,3,5 这几个质因数，所以自然可以拆成这三个数的幂相乘的形式，也就解决了分母的高精危机。详见大佬 123456zmy 的题解 P7113 【排水系统】
~~聪明的放弃最后一个点，在写完 gcd 等一系列分数运算后用 long long 拿到 90pts 卷铺盖走人。~~

2.5 其他运用

刚才说过，拓扑排序在很多图论相关的知识里非常常见，这里就介绍两个：

2.5.1 树上差分

在树上差分后，我们考虑从叶结点向上遍历求子树前缀和。这个过程既可以在 dfs 遍历之后回溯过程中实现，也可以使用拓扑排序来寻找叶结点，这样就类似于拓扑时 DP 了。

2.5.2 博弈论

拓扑排序是解博弈论问题非常关键的一步。 我们经常采用魔改版拓扑排序来判断每个节点的必胜/必败状态.

比如，我们常见类似这样的代码：

while(top) {
	int u=s[top--];
	if(oiw[u]==1) forE(u) {
		if(--mir[v]==0)
			if(!vis[v]) oiw[v]=-1,vis[v]=1,s[++top]=v;
	}
	else for(int p=head[u],v=E[p].to;p;p=E[p].next,v=E[p].to)
		if(!vis[v]) oiw[v]=1,vis[v]=1,s[++top]=v;
}

这里 $oiw$ 表示当前状态是否为 当前出棋者的必胜状态。

在反图中，环在结果一边的出点 出度大于 1.

当 $oiw_u=0$ 时，当前是出棋者的必败状态，则 出点是出棋者的必胜状态。所以无所畏惧，我们将他的 所有出点 入栈，不考虑入度是否清零。即，即使有环，我照样赢。

当 $oiw_u=1$ 时，证明 如果出环，出棋者必输。所以我们考虑将 无入度的出点 入栈。即，我 不能让你进入环内，或者从起点方向说，我 不会选择出环。

这同样也是拓扑排序可以在多种不同的选择中做出最优选择的原理。与环不同的是，多个选择的决定点 出度大于 1. 但异曲同工的是，魔改后的拓扑排序 永远对将当前点判定为出棋者胜的点给予最高优先级。

3. Tarjan 连通分量算法

注：下文中所有的 Tarjan 指 Tarjan 连通分量算法。

不熟悉 Robert E. Tarjan 的同学建议 bdfs 一下，你就会发现他是 信息学超人 了。

按照笔者对 Tarjan 的理解来说，tarjan 连通分量算法的本质是 观察与判断每个点及与其相邻节点在 dfs 树上的性质。

3.1 理论基础

3.1.1 DFS 生成树

dfs 生成树的的边大致分为四种（图片摘自 OI - wiki）：

树边：示意图中以黑色边表示，每次搜索找到一个还没有访问过的结点的时候就形成了一条树边。
反祖边：示意图中以红色边表示（即 $7 \to 1$），也被叫做回边，即指向祖先结点的边。
横叉边：示意图中以蓝色边表示（即 $9 \to 7$），它主要是在搜索的时候遇到了一个已经访问过的结点，但是这个结点 并不是 当前结点的祖先。
前向边：示意图中以绿色边表示（即 $3 \to 6$），它是在搜索的时候遇到子树中的结点的时候形成的。

DFS生成树图解

3.1.2 时间戳与追溯值

对于 $low$ 的解释众说纷纭，这个版本的解释应该是比较原始的解释，和 tarjan 最早的论文里的比较像的那种。

在 dfs 的过程中，Tarjan 算法需要维护两个信息：

$dfn_u$：深度优先搜索遍历时结点 $u$ 被搜索的次序，即 时间戳。
$low_u$：在 $u$ 的子树中能够回溯到的最早的已经在栈中的结点，即 追溯值。设以 $u$ 为根的子树为 $Subtree_u$。$low_u$ 定义为以下结点的 $dfn$ 的最小值：
- $Subtree_u$ 中的结点；
- 从 $Subtree_u$ 通过一条非树边能到达的结点。

DFS 生成树与强连通分量有什么关系呢？

不难得出，如果结点 $u$ 是某个强连通分量在搜索树中遇到的第一个结点，那么这个强连通分量的其余结点肯定是在搜索树中以 $u$ 为根的子树中。结点 $u$ 被称为这个 强连通分量的根。

由此一来，我们还可以得出一些强连通分量的DFS生成树的性质：

一个节点的子树内的节点的 $dfn$ 都大于该节点的 $dfn$。
从根开始的一条路径上的 $dfn$ 严格递增，$low$ 严格非降。

3.2 求有向图的强连通分量

3.2.1 逻辑梳理

在对有向图进行遍历时，将搜索到的节点入栈，并在找到强连通元素时按照该元素包含结点数目让栈中元素出栈。从节点 $u$ 沿树边访问可达的节点 $v$ 时，对于 $dfn_v$，$low_v$ 与 $v$ 的入栈状态，存在三种情况：

$dfn_v$ 未赋值：证明这是第一次访问节点 $v$，为 $dfn_v$ 和 $low_v$ 赋初值，并在回溯时用 $low_v$ 更新 $low_u$。
$dfn_v$ 已赋值，且 $v$ 已在栈中：证明节点 $v$ 已经被访问。用 $dfn_v$ 更新 $low_u$。
$dfn_v$ 已赋值，且 $v$ 不在栈中：证明节点 $v$ 与所在的强连通分量已被处理，无需进行操作。

基于 $dfn$ 与 $low$ 的定义，对于以 $u$ 为根的强连通分量，任意一个非 $u$ 的节点 $v$ 必然满足 $dfn_v<low_v$，且有 $dfn_u=low_u.$ 所以，当我们回溯至满足 $dfn_u=low_u$ 的节点 $u$ 时，栈中 $u$ 及其上方的节点构成一个 强连通元素。

一个大概的过程：

\[\begin{array}{ll} 1 & \textbf{Input. } \text{The edges of the digraph } G=(V,E), \text{ which element in } e \text{ is } (u,v).\\ 2 & \textbf{Output. } \text{The serial number of the SCC to which each vertex belongs in the graph.}\\ 3 & \textbf{Method. }\\ 4 & \textbf{Function } \text{Tarjan} (u)\\ 5 & \qquad tot \gets tot+1,dfn_u \gets tot, low_u \gets tot\\ 6 & \qquad \text{push } u \text{ into the stack}\\ 7 & \qquad \textbf{for } \text{each } (u,v) \in E_u \\ 8 & \qquad \qquad \textbf{if } dfn_v=0\\ 9 & \qquad \qquad \qquad \text{Tarjan} (v)\\ 10 & \qquad \qquad \qquad low_u \gets \min (low_u,low_v)\\ 11 & \qquad \qquad \textbf{else if } v \text{ is in the stack}\\ 12 & \qquad \qquad \qquad low_u \gets \min (low_u,dfn_v)\\ 13 & \qquad \textbf{if } dfn_u = low_u\\ 14 & \qquad \qquad cnt \gets cnt + 1\\ 15 & \qquad \qquad \textbf{while } \text{the stack is not empty}\\ 16 & \qquad \qquad \qquad \text{pop the top element } v \text{ from the stack}\\ 17 & \qquad \qquad \qquad belong_v \gets cnt\\ 18 & \qquad \qquad \qquad \textbf{if } u=v\\ 19 & \qquad \qquad \qquad \qquad \textbf{break}\\ 20 & \textbf{Endfunction}\\ 21 & \textbf{for } \text{each } u \text{ which is root of a SCC }\\ 22 & \qquad \text{Tarjan}(u)\\ 23 & \textbf{return } belong_u \text{ of each vertex } u \text{ in the graph} \end{array} \]

至此，我们了解了通过 Tarjan 算法求有向图的强连通分量的过程。

3.2.2 代码实现

void Tarjan(int u)//对顶点u进行遍历
{
	low[u]=dfn[u]=++tim;//为dfn和low赋初值
	s[++top]=u;//手写栈入栈
	vis[u]=1;//标记入栈
	for(int p=head[u];p;p=edge[p].next)
	{
		int v=edge[p].to;
		if(!dfn[v])
		{
			Tarjan(v);//dfn未赋值，遍历v
			low[u]=min(low[u],low[v]);//更新low
		}
		else if(vis[v])
			low[u]=min(low[u],dfn[v]);//dfn已赋值，且在栈中，直接更新low
	}
	if(low[u]==dfn[u])//搜到强连通元素
	{
		leaf++;
		while(top)
		{
			int v=s[top];
			s[top--]=0;//出栈
			vis[v]=0,belong[v]=leaf;//标记出栈和所在分量
			if(u==v)	break;//强连通元素的全部节点已出栈
		}
	}
}

时间复杂度是 $O(n+m)$，接下来看下模板题 P3387 【模板】缩点。

思路：通过 Tarjan 求所有强连通元素，将每个强连通元素看作一个点，形成一个新图 (即众多大佬使用的说法：染色)。对新图进行拓扑排序，排序时使用DP求出到达该节点的路径的最大点权和。（拓扑结合 DP 详见拓扑排序博客题单 NO.5）

知识基础：Tarjan，拓扑排序，DP。

$\text{ Click to View the Code.}$

#include<bits/stdc++.h>
using namespace std;
const int NMX=1e4+4;
const int MMX=1e5+5;
int s[NMX],top;
int cnt,low[NMX],dfn[NMX],head[NMX],tim,leaf,belong[NMX],tp[NMX],np[NMX],dp[NMX],inde[NMX],ans,n,m;
bool vis[NMX];
vector<int>	edges[NMX];
struct Edge
{
	int from;
	int to;
	int next;
}edge[MMX];
void add(int a,int b)
{
	cnt++;
	edge[cnt].from=a;
	edge[cnt].to=b;
	edge[cnt].next=head[a];
	head[a]=cnt;
}
void Tarjan(int u) 
{
	low[u]=dfn[u]=++tim;
	s[++top]=u;
	vis[u]=1; 
	for(int p=head[u];p;p=edge[p].next)
	{
		int v=edge[p].to;
		if(!dfn[v])
		{
			Tarjan(v);
			low[u]=min(low[u],low[v]);
		}
		else if(vis[v])
			low[u]=min(low[u],dfn[v]);
	}
	if(low[u]==dfn[u])
	{
		leaf++;//为新处理的强连通元素创造节点，提供编号
		while(top)
		{
			int v=s[top];
			s[top--]=0;
			vis[v]=0;
			belong[v]=leaf;//标记每一个点属于哪个强连通元素
			tp[leaf]+=np[v];//将元素内每一点的点权赋给新节点
			if(u==v)	break;
		}
	}
}
void Toposort()//拓上DP，可以参考拓扑排序博客第五题
{
	stack<int> s;
	for(int i=1;i<=leaf;++i)
	{
		dp[i]=tp[i];
		if(!inde[i])	s.push(i);
	}
	while(!s.empty())
	{
		int u=s.top();
		s.pop();
		inde[u]=-1;
		ans=max(ans,dp[u]);
		for(int i=0;i<edges[u].size();++i)
		{
			int v=edges[u][i];
			inde[v]--;
			dp[v]=max(dp[v],dp[u]+tp[v]);
			if(!inde[v])	s.push(v);
		}
	}
}
int main()
{
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;++i)
		scanf("%d",&np[i]);
	for(int i=1;i<=m;++i)
	{
		int u,v;
		scanf("%d%d",&u,&v);
		add(u,v);
	}
	for(int i=1;i<=n;++i)//对所有点Tarjan
		if(!dfn[i])
		{
			tim=0;
			Tarjan(i);
		}
	for(int i=1;i<=cnt;++i)//为新节点建边
	{
		if(belong[edge[i].from]!=belong[edge[i].to])
		{
			edges[belong[edge[i].from]].push_back(belong[edge[i].to]);
			inde[belong[edge[i].to]]++;
		}
	}
	Toposort();
	printf("%d",ans);
	return 0;
}

3.2.3练习

3.2.3.1 P2341 [USACO03FALL / HAOI2006] 受欢迎的牛 G

这道题也不难啊，推理过程如下：

牛 $u$ 喜欢牛 $v$ 其实可以看作是从 $u$ 至 $v$ 的一条有向边。由此易证，在所有牛 $V$ 与他们之间的喜欢关系 $E$ 形成的图 $G=(V,E)$ 中，如果存在一个牛的集合 $H \subset G$，且 $H$ 中的任意两只牛都互相喜欢，则 $H$ 实际上是 $G$ 的一个强连通分量。
如果强连通分量中的一只牛是明星，根据强连通分量的定义，则该分量中的每一只牛都是明星。故可以对 $G$ 进行缩点，将每个强连通元素看作一个点处理，且该点的点权为元素内点的数量
对于染色缩点后的新图 $G$ 中的任意节点 $u$，若染色 $u$ 的牛想成为明星，面对如下情况：

$u$ 有入度且有出度：不可能成为明星。因为 $u$ 不与其他点强连通，所以若有一条边 $u \to v$，则不可能存在边 $v \to u$。故染色 $u$ 的牛必然不被所有牛喜欢。

$u$ 无入度：不可能成为明星。一直在喜欢别人，没人喜欢他。（悲）

$u$ 无出度：视无出度的点决定：无出度的点多于 1，必然存在点 $u$ 和 $v$ 来回方向都不可达；无出度的点等于 1，在该无出度点有入度的情况下，则易证图 $G$ 内的任意节点都可达该节点。染色该点的所有牛都为明星。

由此得出，想知道牛的明星个数，找无出度的点就好了。若无出度点多于一，则该图无明星；若无出度点等于一，则该图的明星数即为染色该点的牛的数量。

该题解决。

$\text{ Click to View the Code.}$

#include<bits/stdc++.h>
using namespace std;
const int NMX=1e4+4;
const int MMX=5e4+4;
int s[NMX],top;
int cnt,low[NMX],dfn[NMX],head[NMX],tim,ans,n,m;
int val[NMX],leaf,belong[NMX],outde[NMX];
bool vis[NMX];
struct Edge
{
	int from;
	int to;
	int next;
}edge[MMX];
void add(int a,int b)
{
	cnt++;
	edge[cnt].from=a;
	edge[cnt].to=b;
	edge[cnt].next=head[a];
	head[a]=cnt;
}
void Tarjan(int u) 
{
	low[u]=dfn[u]=++tim;
	s[++top]=u;
	vis[u]=1; 
	for(int p=head[u];p;p=edge[p].next)
	{
		int v=edge[p].to;
		if(!dfn[v])
		{
			Tarjan(v);
			low[u]=min(low[u],low[v]);
		}
		else if(vis[v])
			low[u]=min(low[u],dfn[v]);
	}
	if(low[u]==dfn[u])
	{
		leaf++;
		while(top)
		{
			int v=s[top];
			s[top--]=0;
			vis[v]=0;
			belong[v]=leaf;
			val[leaf]++;
			if(u==v)	break;
		}
	}
}
int main()
{
	scanf("%d%d",&n,&m);
	for(int i=1;i<=m;++i)
	{
		int a,b;
		scanf("%d%d",&a,&b);
		add(a,b);
	}
	for(int i=1;i<=n;++i)
		if(!dfn[i])
			Tarjan(i);
    for(int u=1;u<=n;++u)//遍历所有边
		{
			for(int i=head[u];i;i=edge[i].next)
			{
				int v=edge[i].to;
				if(belong[u]!=belong[v])
					outde[belong[u]]++;//计算出度
			}
		}
	bool flag=0;
	for(int i=1;i<=leaf;++i)//leaf:染色的颜色数量
	{
		if(!outde[i])
		{
			if(!flag)	{flag=1;	ans=val[i];}//第一个无出度的点，作为结果
			else	{printf("0");	return 0;}//出现第二个无出度的点，该图无明星
		}
	}
	printf("%d",ans);
	return 0;
}

3.2.3.2 P1073 [NOIP2009 提高组] 最优贸易

这道题的缩点和拓扑排序与 P3387 【模板】缩点、P2341 [USACO03FALL / HAOI2006] 受欢迎的牛 G 没有什么大的区别，重点就在于 DP。

我们需要找到同一条路径上的最大点权差，且点权小的节点可达点权大的节点。（大点位置先于小点，先买后卖，买低卖高。）主要是面临如下问题：

大点权和小点权不在同一条路径上——必须同时更新大小点权。（由于动态规划的无后效性，只需考虑最大点权差，无需考虑来自哪条路径。）
大点权的位置先于小点权——必须保证更新的小点权在大点权前。

在面对这类问题时，我们采用两个变量维护结果：

$mn_i$：存储从 $1$ 至 $i$ 位出现的最小点权；
$dp_i$：存储第 $i$ 个点的最大点权差；

由于在本题中，我们进行了缩点操作，每个点可能同时存在两个点权（代表染色该点的强连通分量的最小点权和最大点权），所以我们实际用到了如下变量：

变量名	意义
$mx$	染色该点的最大点权
$mn$	染色该点的最小点权
$maxcost$	染色该点的最大点权差
$mincost$	到达该点时出现的最小点权
$dp$	到达该点的所有路径中的最大点权差

我们的最终结果的得到 dp 值，状态转移时将原结果与该点计算出的最新结果比较。为了是小点权的位置大于大点权，我们先处理目前出现过的最小点权，然后通过该最小点权得出最新结果进行更新。

废话不多说，上状态转移公式。
对于一条边 $u\to v$，状态转移如下：

\[mincost_v=\min(mincost_u,mn_v) \]

\[dp_v=\max(\max(dp_u,dp_v),\max(maxcost_v,mx_v-mincost_v)) \]

这个方法适用于所有该类题型：先更新该点前的最小点权，用该点点权与最小点权的差更新该点结果。

$\text{ Click to View the Code.}$

#include<bits/stdc++.h>
using namespace std;
const int NMX=1e5+5;
const int MMX=5e5+5;
int s[NMX],top;
int cnt,low[NMX],dfn[NMX],head[NMX],val[NMX],dep,leaf,belong[NMX],inde[NMX],n,m;
int mn[NMX],mx[NMX],maxcost[NMX],mincost[NMX],dp[NMX];
bool vis[NMX];
vector<int> edges[NMX];
struct Edge
{
	int to;
	int next;
}edge[MMX];
void add(int a,int b)
{
	cnt++;
	edge[cnt].to=b;
	edge[cnt].next=head[a];
	head[a]=cnt;
}
void read()//读入
{
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;++i)
		scanf("%d",&val[i]);
	for(int i=1;i<=m;++i)
	{
		int x,y,z;
		scanf("%d%d%d",&x,&y,&z);
		add(x,y);
		if(z-1)
		add(y,x);
	}
}
void Tarjan(int u)//日常塔扬
{
	low[u]=dfn[u]=++dep;
	s[++top]=u;
	vis[u]=1;
	for(int p=head[u];p;p=edge[p].next)
	{
		int v=edge[p].to;
		if(!dfn[v])
		{
			Tarjan(v);
			low[u]=min(low[u],low[v]);
		}
		else if(vis[v])
			low[u]=min(low[u],dfn[v]);
	}
	if(low[u]==dfn[u])
	{
		leaf++;
		mx[leaf]=val[u];
		mn[leaf]=val[u];
		while(top)
		{
			int v=s[top];
			s[top--]=0;
			vis[v]=0;
			belong[v]=leaf;
			mx[leaf]=max(mx[leaf],val[v]);
			mn[leaf]=min(mn[leaf],val[v]);
			if(u==v)	break;
		}
		maxcost[leaf]=mx[leaf]-mn[leaf];
	}
}
void compress()//缩点染色
{
	for(int i=1;i<=n;++i)
		if(!dfn[i])
			Tarjan(i);
	for(int u=1;u<=n;++u)
	{
		for(int i=head[u];i;i=edge[i].next)
		{
			int v=edge[i].to;
			if(belong[u]!=belong[v])
			{
				edges[belong[u]].push_back(belong[v]);
				inde[belong[v]]++;
			}
		}
	}
}
void Toposort()//拓扑DP
{
	stack<int> s;
	for(int i=1;i<=leaf;++i)
	{
		if(!inde[i])	s.push(i);
	}
	mincost[s.top()]=mn[s.top()];
	while(!s.empty())
	{
		int u=s.top();
		s.pop();
		for(int i=0;i<edges[u].size();++i)
		{
			int v=edges[u][i];
			inde[v]--;
			mincost[v]=min(mincost[u],mn[v]);
			dp[v]=max(max(dp[v],dp[u]),max(maxcost[v],mx[v]-mincost[v]));
			if(!inde[v])	s.push(v);
		}
	}
}
int main()
{
	read();
	compress();
	Toposort();
	printf("%d",dp[belong[n]]);
	return 0;//优雅回城
}

3.2.3.3 P2863 [USACO06JAN]The Cow Prom S

数数而已，非常简单。

3.3 求无向图的割点与桥

注：下文中提到的追溯指寻找追溯值这一过程，即追溯到的时间戳必须满足 $low$ 的定义。

3.3.1 割点

我们对一个无向图进行遍历，观察每个节点时间戳和追溯值的性质。

为方便理解，我们借用 OI - WIKI 的图来举个例子：

遍历前无向图例

对该图进行遍历，同时标记时间戳和追溯值，可以得到下图：（图中标记红色标记为时间戳）

遍历后无向图例

不难看出图中 $2$ 是割点。通过比较时间戳和追溯值，我们总能得到如下结论：

对于某个节点 $u$ ，至少存在一个子节点 $v$，满足：

\[dfn_u \leq low_v \]

则 $u$ 是割点。

这个公式可以解释为，以 $v$ 为根的子树 $Subtree_v$ 最早只能追溯到节点 $u$ 时间戳比 $u$ 大的节点，这意味着在点 $u$ 被删去后原图将被分割成两部分，（其中一部分即为 $Subtree_v$。）这满足割点的定义。

但请特别注意，该结论不适用于 根节点。对于根节点，我们用到的特殊判定方法如下：

若 $u$ 是 搜索树 的根节点，且 $u$ 只有一个子节点，则 $u$ 是割点。

这可以解释为，如果 $u$ 不是割点，则通过 $u$ 的任意一个子节点 $v$ 都可以到达其他节点，这是在搜索树中，$u$ 仅向下搜索一次，即只有一个子节点。所以，当 $u$ 在搜索树中的子节点超过一个时，可以表明删去 $u$ 后该图必然分成多个部分。（每个部分即以 $u$ 的一个子节点为根节点的搜索树内的所有节点）

void tarjan(int u,int fa)//对根节点特判，所以要记住根节点是谁，传参需要多传一个fa 
{
	dfn[u]=low[u]=++dep;
	int child=0;//子节点数量 
	for(int i=0;i<edges[u].size();++i)
	{
		int v=edges[u][i];
		if(!dfn[v])
		{
			tarjan(v,fa);
			low[u]=min(low[u],low[v]);
			if(u!=fa && dfn[u]<=low[v] && !cut[u])//不是根节点，符合判定公式，是割点；若未被标记，进行标记。 
				cut[u]=1,ans++;
			if(u==fa)
				child++;
		}
		low[u]=min(low[u],dfn[v]);//不需要栈维护，所以不用检查入栈情况。 
	}
	if(child>1 && u==fa && !cut[u])//根节点，子节点多于一，是割点；若未被标记，进行标记。
		cut[u]=1,ans++;
}

3.3.2 桥

桥基本与割点相同。不同的是，判定公式为：

\[dfn_u < low_v \]

这点不同在于，删掉割点，会连通删掉与其相关的所有边。所以，能够追溯到节点 $u$ 的子节点 $v$ 的子树在删掉 $u$ 后也会被与原图分割。但删掉桥，对节点没有影响。所以，在删掉 $u\to v$ 后 $v$ 仍可以通过追溯时用到的那条边回到 $u$，$u\to v$ 自然就不是桥了。且因为对节点没有影响，我们也不需要对根节点相关的边使用特殊的判定方法。

void tarjan(int u)
{
	dfn[u]=low[u]=++dep;
	for(int i=0;i<edges[u].size();++i)
	{
		int v=edges[u][i];
		if(!dfn[v])
		{
			tarjan(v);
			low[u]=min(low[u],low[v]);
			if(dfn[u]<low[v])
			{
				cutx[++cnt]=u;
				cuty[cnt]=v;
			}
		}
		low[u]=min(low[u],dfn[v]);
	}
}

3.3.3 练习

3.3.3.1 模板题

非常纯粹的模板。因为求割点和桥都是求单个元素，而不是求元素的集合，所以 不需要中间容器。

$\text{ Click to View the AC Code.}$

#include<bits/stdc++.h>
using namespace std;
const int NMX=2e4+4;
int dfn[NMX],low[NMX],dep;
bool cut[NMX];//判定是否为割点 
int n,m,ans;
vector<int> edges[NMX];//存图，链式前向星也是可以的 
void tarjan(int u,int fa)//对根节点特判，所以要记住根节点是谁，传参需要多传一个fa 
{
	dfn[u]=low[u]=++dep;
	int child=0;//子节点数量 
	for(int i=0;i<edges[u].size();++i)
	{
		int v=edges[u][i];
		if(!dfn[v])
		{
			tarjan(v,fa);
			low[u]=min(low[u],low[v]);
			if(u!=fa && dfn[u]<=low[v] && !cut[u])//不是根节点，符合判定公式，是割点；若未被标记，进行标记。 
				cut[u]=1,ans++;
			if(u==fa)
				child++;
		}
		low[u]=min(low[u],dfn[v]);//不需要栈维护，所以不用检查入栈情况。 
	}
	if(child>1 && u==fa && !cut[u])//根节点，子节点多于一，是割点；若未被标记，进行标记。
		cut[u]=1,ans++;
}
int main()
{
	scanf("%d%d",&n,&m);
	for(int i=1;i<=m;++i)
	{
		int a,b;
		scanf("%d%d",&a,&b);
		edges[a].push_back(b);
		edges[b].push_back(a);//双向存图 
	}
	for(int i=1;i<=n;++i)
		if(!dfn[i])
			tarjan(i,i);
	printf("%d\n",ans);
	for(int i=1;i<=n;++i)
		if(cut[i])
			printf("%d ",i);
	return 0;
}

3.3.3.2 POJ-1144 Network

我挂的还是 vjudge 的链接啊,主要还是读入有点恶心。

3.3.3.3 P3469 [POI2008]BLO-Blockade

这道题实在是不好说，，，哭辽，以前没见过的题型。去看题解吧别看我，我也不想讲这道题了，，，真的很抽象，，，公式这种东西真的只可意会不可言传。就嘱咐一声，结果用 long long。

3.3.3.4 POJ-3352 Road Construction

3.4 求无向图的点/边双连通分量

3.4.1 v-DCC

v-DCC 即 BCC，点双连通分量。

3.4.1.1 逻辑梳理

首先我们要知道一个图中的哪些子图是一个 BCC。上图：

通用图例

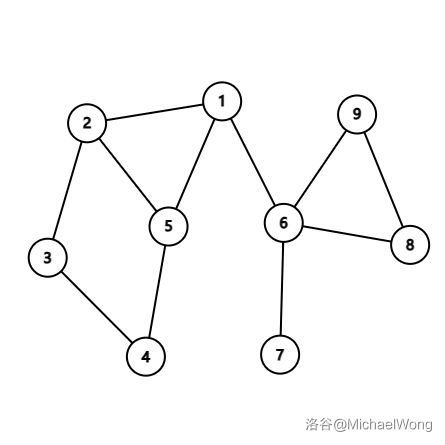
如图，在该图中，共有：

四个 BCC。可以注意到，割边本身也是一个 BCC。

我们对该图进行遍历，同时标记时间戳和追溯值，可以得到下图：（图中节点序号即为时间戳，“[ ]” 中为追溯值，灰色节点为割点。）

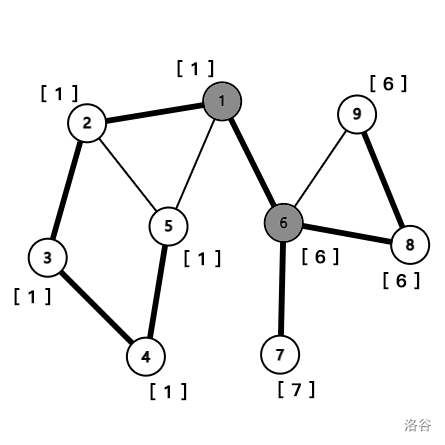
通用图例遍历后

我们不难看出，BCC 与割点息息相关。与求有向图的强连通分量相似，我们在求无向图的 BCC 时也采用栈来存储已遍历的节点。每当搜索到一个割点 $u$，栈中 $u$ 及其上方的节点就构成一个 BCC。

需要注意的是，搜索到的节点虽然算入新的 BCC 中，但他 并不出栈，他将继续进行下面其他子树的搜索任务。这个割点要一直等到回溯至他在搜索树中的上一个前驱割点时，作为该前驱割点的栈上方节点出栈。

值得一提的是，与有向图不同，对于无向图，我们在通过 $dfn_v$ 更新 $low_u$ 值时，不需要 考虑 $v$ 是否 在栈中。在有向图时，$u$ 指向不在栈中的元素 $v$，证明 $v$ 必不可达 $u$，故不可对 $low_u$ 进行更新；但在无向图中，$u$ 可达 $v$ 则 $v$ 必然可达 $u$，所以可以更新。（但是需要判定该边的另一个节点不是这个点在搜索树上的父亲节点，即这条边不是刚刚走过的树边，求 e-DCC 同理。）

此外，因为割边的两个节点必然都是割点，所以其中一个点在栈中的上方节点必然 有且只有 另一个节点。这样一来，割边 不需要进行特殊判定 就可以直接解决。

在判断割点时，是需要对根节点进行特判的。这是根据割点判定公式，根节点必然被判定为割点。但是在该方法中，根节点同样不需要特殊判定。因为即使根节点永远被判定成割点，在本次出栈中，他仍 不出栈，他也确实应该被算在他栈上方的所有 BCC 中。我们也不难得知，在整个搜索过程结束后，根节点仍然 在栈中，因为他 没有前驱割点。

3.4.1.2 代码实现

P8435 【模板】点双连通分量

如题中所说，请认真考虑孤立点与自环的情况。

$\text{AC Code}$：

#include<bits/stdc++.h>
using namespace std;
const int NMX=5e5+5;
int dfn[NMX],low[NMX],dep;
int s[NMX],top; 
int n,m,ans;
int cn;//BCC数量 
vector<int> edges[NMX],bcc[NMX];//存图，存BCC 
void tarjan(int u,int rt)//rt对孤立点处理 
{
	dfn[u]=low[u]=++dep;
	s[++top]=u;
	if(u==rt && !edges[u].size())
		bcc[++cn].push_back(u);//根节点，无边，是孤立点
	for(int i=0;i<edges[u].size();++i)
	{
		int v=edges[u][i];
		if(!dfn[v])
		{
			tarjan(v,rt);
			low[u]=min(low[u],low[v]);
			if(dfn[u]<=low[v])
			{
				cn++;
				int w;
				do
				{
					w=s[top--];
					bcc[cn].push_back(w);
				}while(w!=v);
				bcc[cn].push_back(u);
			}//遇割点，出栈。出栈操作可参考有向图的强连通分量 
		}
		else low[u]=min(low[u],dfn[v]);//不考虑是否在栈中，直接更新 
	}
}
int main()
{
	scanf("%d%d",&n,&m);
	for(int i=1;i<=m;++i)
	{
		int a,b;
		scanf("%d%d",&a,&b);
		if(a!=b)
		{
			edges[a].push_back(b);
			edges[b].push_back(a);
		}//判断自环，双向建边 
	}
	for(int i=1;i<=n;++i)
		if(!dfn[i])
			tarjan(i,i);
	printf("%d\n",cn);
	for(int i=1;i<=cn;++i)
	{
		printf("%d",bcc[i].size());
		for(int j=0;j<bcc[i].size();++j)
			printf(" %d",bcc[i][j]);
		printf("\n");
	}
	return 0;
}

3.4.2 e-DCC

e-DCC 即边双连通分量。

3.4.2.1 逻辑梳理

还是这个图，我们可以找到里面的 e-DCC：

通用图例遍历后

1 2 3 4 5
6 8 9
7

共3个 e-DCC。可以注意到，割边不是 e-DCC（因为删掉割边后两个点不连通），而单独一个点可以作为 e-DCC。

与 BCC 相似，e-DCC 与割边密切相关。一张图删掉所有割边后的每一个极大子图都是该图的一个 e-DCC。

所以到这里，思路就已经十分清晰了。我们只需要先找出割边并标记，再删去割边重新遍历一遍，找到每个极大子图即可。

3.4.2.2 代码实现

P8436 【模板】边双连通分量

对于割边标记，链式前向星可以选择为边标记不同的权重，邻接表存图则可以通过哈希。（如果有卡 std::map 的情况可以手写哈希。）

我是使用的是 std::vector + hash，下面是 $\text{AC Code}$：

#include<bits/stdc++.h>
#define E(x,y) (long long)min(x,y)*1e6+(long long)max(x,y)//给边建立一个二维数列到数字的映射方式 
using namespace std;
const int mod=150000;
const int NMX=5e5+5;
int n,m;
int dfn[NMX],low[NMX],dep;
bool vis[NMX];
int cnt=0;
vector<int> edges[NMX],ans[NMX];
struct Hash
{
	vector<long long> vt1[200000];
	vector<short> vt2[200000];
	short& operator [](long long k)
	{
		int t=k%mod;
		for(int l=0;l<vt1[t].size();++l)
			if(vt1[t][l]==k)
				return vt2[t][l];
		vt1[t].push_back(k);
		vt2[t].push_back(0);
		return vt2[t].back();
	}
}hash1,hash2;//手写哈希，hash1判断桥，hash2判断重边 
void tarjan(int fa,int u)
{
	dfn[u]=low[u]=++dep;
    for(int l=0;l<edges[u].size();++l)
    {
        int v=edges[u][l];
        if(!dfn[v])
        {
            tarjan(u,v);
            low[u]=min(low[u],low[v]);
            if(dfn[u]<low[v] && !hash2[E(u,v)]-1)
                hash1[E(u,v)]=1;//不重边，符合条件，是桥 
        }
        if(v!=fa || hash2[E(u,v)]-1)	low[u]=min(low[u],dfn[v]);//重边或不是树边，更新low值 
    }
}
void dfs(int u)
{
	vis[u]=1;
	ans[cnt].push_back(u);
	for(int l=0;l<edges[u].size();++l)
	{
		int v=edges[u][l];
		if(!vis[v] && !hash1[E(u,v)])//没访问过，不是桥，进行遍历 
			dfs(v);
	}
	return;
}//重新DFS得出每个极大子图 
int main()
{
	scanf("%d%d",&n,&m);
	for(int i=1;i<=m;++i)
	{
		int u,v;
		scanf("%d%d",&u,&v);
		if(u!=v)
		{
			edges[u].push_back(v);
			edges[v].push_back(u);
			hash2[E(u,v)]++;//判重边 
		}//判断自环，双向建边 
	}
	for(int i=1;i<=n;++i)
		if(!dfn[i])
			tarjan(0,i);
	for(int i=1;i<=n;++i)
		if(!vis[i])
			cnt++,dfs(i);
	printf("%d\n",cnt);
	for(int i=1;i<=cnt;++i)
	{
		printf("%d",ans[i].size());
		for(int j=0;j<ans[i].size();++j)
			printf(" %d",ans[i][j]);
		puts("");
	}
    return 0;
}

4. 最短路

4.1 三角形不等式

首先我们介绍一些基本概念。

由于是单源最短路，我们定义一个起点 $s$，$dis_u$ 表示起点 $s$ 到节点 $u$ 的最短路长度。

一般来讲，对于一条为 $w$ 的边 $u \to v$，如果目前的最短路是正确的，都应该满足：

\[dis_u+w \geq dis_v \]

我们称之为 三角形不等式。

对于不满足三角形不等式的，我们就要更新最短路了：

一条边权为 $w$ 的边 $u \to v$，如果满足 $dis_u+w<dis_v$，即可用 $dis_u+w$ 更新 $dis_v$。

这个更新的过程叫做松弛。

松弛是所有最短路算法的基本操作。

4.2 单源最短路径

4.2.1 Bellman-Ford

最基本的最短路算法。一个非常朴素的想法，朴素到其复杂度为 $O(VE)$，本质就是对每一条边都尝试松弛。因为其复杂度过于高，实际用途已经基本废了。所以主要介绍其优化后的算法，SPFA。

4.2.2 SPFA

Shortest Path Faster Algorithm, AKA SPFA。

实际上，这个名字只在大陆存在。因为他实际上叫做 队列优化的 Bellman-Ford 算法。顾名思义，使用队列来优化 Bellman-Ford，本质思想还是朴素的对每个边进行松弛，而且——

\[\text{关于 SPFA, }\textbf{他死了。} \]

（这个帖子足见杀他的方法已经发展得很完备了。）

所以直接上模板题代码吧。

UPD 2023.7.1 在网络流里，SPFA 活得熠熠生辉！（虽然只在网络流里是这样。）

$Code$：

#include<bits/stdc++.h>
const int N=1e4+5;
int n,m,s,dis[N];
bool vis[N];
struct Edge	{int to,w;};
std::vector<Edge> E[N];
void SPFA(int start){
	std::queue<int> q;
	for(int i=1;i<=n;++i)
		dis[i]=INT_MAX;
	vis[start]=1,dis[start]=0;
	q.push(start);
	while(!q.empty()){
		int u=q.front();
		q.pop();
		vis[u]=0;
		for(auto v:E[u]){
			if(dis[u]+v.w<dis[v.to]){
				dis[v.to]=dis[u]+v.w;
				if(!vis[v.to]){
					vis[v.to]=1;
					q.push(v.to);
				}
			}
		}
	}
}
int main(){
	std::ios::sync_with_stdio(0);
	std::cin.tie(0);std::cout.tie(0);
	std::cin>>n>>m>>s;
	for(int i=1;i<=m;++i){
		int u,v,w;
		std::cin>>u>>v>>w;
		E[u].push_back({v,w});
	}
	SPFA(s);
	for(int i=1;i<=n;++i)
		std::cout<<dis[i]<<" ";
	return 0;
}

SPFA 的复杂度一般是 $O(kE)$ 的，但是在一些特殊图（如网格图和链套菊花）中会退化到 $O(nm)$，所以，慎用。

*最后的用武之地 - 判断负环

在 SPFA 中，一个节点最多被松弛 $n$ 次。所以，我们可以记录每个节点 $u$ 被松弛的次数 $sum_u$，如果出现 $sum_n>n$，就可以判定出现负环了。

$\textbf{SPFA}$ - OI 迅

SPFA 是写最短路径而不用堆优化的唯一的人。

他身材很高大；青白脸色，皱纹间时常夹些伤痕；

一部乱蓬蓬的花白的胡子。穿的虽然是女装，可是又脏又破，似乎十多年没有补，也没有洗。

他对人说话，总是满口 $\Theta(kE)$，叫人半懂不懂的。

因为他姓 S，别人便从描红纸上的“$\texttt{Shortest Path Faster Algorithm}$”这半懂不懂的话里，替他取下一个绰号，叫作 SPFA。

SPFA 一到机房，所有写代码的人便都看着他笑，有的叫道，“SPFA，你又 TLE 了！”

他不回答，对我说，“打 $1e5$ 个结点，要 $2e5$ 条边。”便排出一条队列。

他们又故意的高声嚷道，“你一定又被出题人卡了！”SPFA 睁大眼睛说，“你怎么这样凭空污人清白……”

“什么清白？我前天亲眼见你被出题人卡到 $O(nm)$，吊着打。”

SPFA 便涨红了脸，额上的青筋条条绽出，争辩道，“TLE 不能算 $O(nm)$……$O(nm)$！

“卡常数的事，能算 $O(nm)$ 么？”接连便是难懂的话，什么“SPFA 的复杂度是 $\Theta(kE)$”，什么“可以证明 $k$ 一般小于等于 $2$”之类。

引得众人都哄笑起来；机房内外充满了快活的空气。

现在，我已经一年没看见也没听别人说过 SPFA，SPFA 大抵是死了吧！

4.2.3 Dijkstra

我们的老朋友迪科斯彻，最常用的单源最短路算法，和二叉堆优化的 B-F 算法的唯一区别是 Dijkstra 中每个节点只作为媒介节点参与松弛一次。

将有向带权图 $G=(V,E)$ 的点集 $V$ 分为两个集合：$S$ 和 $T$，$S$ 中的点已确定最短路径长度，而 $T$ 中的点没有确定。一开始所有点 $u$ 都在 $T$ 集合中，$dis_u$ 赋初值 $+ \infty$，只有起点 $s \in S, dis_s=0$。迪科斯彻采用贪心的思想，在 $S$ 中选择 $dis_u$ 最小的节点 $u$，对 $u$ 可达的所有 $v \in T$ 进行松弛。

可以证明，$u$ 仅需作为 媒介节点 参与松弛一次，$u$ 作为媒介节点后 $dis_u$ 不可能再改变。

实现时，我们考虑采用 std::priority_queue 维护，最坏对 $m$ 条边进行松弛，优先队列单次操作复杂度 $O(\log n)$，但由于部分节点可能会多次被松弛，从而重复入队，所以其实优先队列中最多有 $m$ 个点，复杂度为 $O(\log m)$，所以总复杂度 $O(m \log m)$，也非常优秀了。

接下来是模板题单源最短路径（标准版）的 $Code$：

#include<bits/stdc++.h>
const int N=1e5+5;
struct Edge { int to,w;
	bool operator < (const Edge &a) const {return w>a.w;}
};
std::vector <Edge> E[N];//使用结构体和vector存边
int n,m,s,dis[N];
bool flag[N];
void Dijkstra(int start)
{
	memset(dis,0x3f,sizeof dis);
	std::priority_queue <Edge> q;
	dis[start]=0;
	q.push({start,0});
	while(!q.empty()){
		int u=q.top().to;
		q.pop();
		if(flag[u])	continue;
		/*每个点仅一次作为媒介节点参与松弛。*/
		flag[u]=1;
		for(auto v:E[u]){
			if(dis[u]+v.w<dis[v.to]){
				dis[v.to]=dis[u]+v.w;//松弛
				q.push({v.to,dis[v.to]});//入集合S
			}
		}
	}
}
int main()
{
	std::ios::sync_with_stdio(0);
	std::cin.tie(0);std::cout.tie(0);
	std::cin>>n>>m>>s;
	for(int i=1;i<=m;++i){
		int u,v,w;
		std::cin>>u>>v>>w;
		E[u].push_back({v,w});
	}
	Dijkstra(s);
	for(int i=1;i<=n;++i)
		std::cout<<dis[i]<<" ";
	return 0;
}

但是呢，Dijkstra 不能用于负环。因为在 Dijkstra 中，每一个顶点作为媒介节点参与松弛操作只有一次，所以得出的结果其实是松弛一次的结果，且无法进行判断其是否是负环。

同时，存在 负边权 的图也不可使用 Dijkstra。

4.3 多源最短路径 - Floyd

OK，现在我们来说一下最后的，多源最短路径。解决他的算法是 Floyd.

其实这个 Floyd 就是一个动态规划，使用邻接矩阵 $dis(i,j)$ 表示从 $i$ 到 $j$ 的最短路径长，枚举每一个节点 $k$，判断其是否满足三角形不等式，不满足就 $dis(i,j) \gets dis(i,k)+dis(k,j)$。

$Code:$

for(int k=1;k<=n;++k){
	for(int i=1;i<=n;++i){
    	for(int j=1;j<=n;++j){
        	dis[i][j]=std::min(dis[i][j],dis[i][k]+dis[k][j]);
		}
	}
}

Floyd 是敲着最简单的，但是 $O(n^3)$ 的复杂度，所以小一点的图哪怕单源也可以凑合用，要是图很大就慎重吧。

5. 生成树

注：本部分旨在速通，复习用，不是很详细。

5.1 最小生成树 - MST

5.1.1 性质

就是：

对于一个无向连通图 $G=(V,E)$，点集 $U \subsetneq V $ 和边集 $A=\{ u \leftrightarrow v|u \in U,v \in (V-U) \} \subsetneq E$，有无向边 $u \leftrightarrow v \in A$ 且在 $A$ 中边权 $w_{u,v}$ 最小，则这条边必然在该图 $G$ 的一棵最小生成树中。

5.1.2 Prim

将无向连通图 $G=(V,E)$ 分为两个集合：已处理 $A$ 和未处理 $B$。处理的过程如下：

将一个节点 $u$ 放入集合 $A$；
在边集 $C=\{ i \leftrightarrow j | i \in A,j \in B\}\subset E$ 寻找最小的一条边，将这条边纳入最小生成树；
重复第 2 步，直至 $B= \varnothing$。

Prim 更适合 稠密图。

$\text{Code - with Prim by Adjacency List, } 1.19 s \text{ without O2}$

#include<bits/stdc++.h>
const int MAXN=5005,inf=0x3f3f3f3f;
int n,m,sp[MAXN],dis[MAXN][MAXN];
bool flag[MAXN];
int prim() {
    int ans=0,tot=0; sp[0]=inf,flag[1]=1;
    for(int i=2;i<=n;++i) sp[i]=dis[1][i];
    for(int i=1;i<n;++i) {
    	int tmp=0;
        for(int v=1;v<=n;++v) if(!flag[v] && sp[v]<sp[tmp]) tmp=v;
        if(!tmp) break;
        ans+=sp[tmp],flag[tmp]=1,++tot;
        for(int l=1;l<=n;++l) if(!flag[l] && dis[tmp][l]<sp[l]) sp[l]=dis[tmp][l];
    }
    return tot==n-1?ans:-1;
}
int main() {
	std::ios::sync_with_stdio(false);
	std::cin.tie(nullptr); std::cout.tie(nullptr);
    std::cin>>n>>m; memset(dis,0x3f,sizeof dis);
    for(int i=1,u,v,w;i<=m;++i) { std::cin>>u>>v>>w; dis[u][v]=dis[v][u]=std::min(dis[u][v],w); }
    int ans=prim();
	if(~ans) std::cout<<ans<<'\n';
	else std::cout<<"orz\n";
	return 0;
}

下面是前向星 prim. 与邻接矩阵不同的是，邻接矩阵需要判断重边，$sp$ 就可以直接赋值；而前向星不需要判断重边，所以 $sp$ 需要取所有边中的最小值。

$\text{Code - with Prim by Forward Star, } 474 ms \text{ without O2}$

#include<bits/stdc++.h>
#define ll long long
#define ld long double
#define fsp(x) std::fixed<<std::setprecision(x)
#define forE(u) for(int p=head[u],v=E[p].to;p;p=E[p].next,v=E[p].to)
const int N=5005,M=2e5+5,inf=0x3f3f3f3f;
int cnt,head[N];
struct edge { int to,next,w; } E[M<<1];
void add(int u,int v,int w) { E[++cnt].to=v,E[cnt].w=w,E[cnt].next=head[u],head[u]=cnt; }
int n,m,sp[N];
bool flag[N];
int prim() {
	memset(sp,0x3f,sizeof sp);
	int ans=0,tot=0; flag[1]=1;
	forE(1) sp[v]=std::min(sp[v],E[p].w);
	for(int i=1;i<=n;++i) {
		int tmp=0;
		for(int v=1;v<=n;++v) if(!flag[v] && sp[v]<sp[tmp]) tmp=v;
		if(sp[tmp]==inf) break;
		ans+=sp[tmp],flag[tmp]=1,++tot;
		forE(tmp) sp[v]=std::min(sp[v],E[p].w);
	}
	return tot==n-1?ans:-1;
}
int main() {
	std::ios::sync_with_stdio(false);
	std::cin.tie(nullptr); std::cout.tie(nullptr);
	std::cin>>n>>m;
	for(int i=1,u,v,w;i<=m;++i) { std::cin>>u>>v>>w; add(u,v,w),add(v,u,w); }
	int ans=prim();
	if(~ans) std::cout<<ans<<'\n';
	else std::cout<<"orz\n";
	return 0;
}

5.1.3 Kruskal

基于贪心的思想，使用并查集维护状态（一个集合一棵树），将所有边从小到大排序后遍历，如果两个点不在同一棵树上，则将该边纳入 MST，合并这条边连通的两个端点的集合。

Kruskal 更适合 稀疏图。

$\text{Code - with Kruskal by Forward Star and Disjoint Set Union, } 230 ms \text{ without O2}$

#include<bits/stdc++.h>
#define ll long long
#define ld long double
const int N=5005,M=2e5+5;
struct edge { int from,to,w; } E[M];
void add(int u,int v,int w,int ord) { E[ord].from=u,E[ord].to=v,E[ord].w=w; }
int n,m,fa[N];
void init() { for(int i=1;i<=n;++i) fa[i]=i; }
int get(int x) { return fa[x]==x?x:fa[x]=get(fa[x]); }
void merge(int x,int y) { fa[get(y)]=get(x); }
int kruskal() {
	init();
	std::sort(E+1,E+m+1,[](const edge &a,const edge &b){ return a.w<b.w; });
	int ans=0,tot=0; edge *it=E;
	while(++it<E+m+1) {
		if(get(it->from)==get(it->to)) continue;
		ans+=it->w,merge(it->from,it->to),tot++;
		if(tot==n-1) break;
	}
	return tot==n-1?ans:-1;
}
int main() {
	std::ios::sync_with_stdio(false);
	std::cin.tie(nullptr); std::cout.tie(nullptr);
	std::cin>>n>>m;
	for(int i=1,u,v,w;i<=m;++i) { std::cin>>u>>v>>w; add(u,v,w,i); }
	int ans=kruskal();
	if(~ans) std::cout<<ans<<'\n';
	else std::cout<<"orz\n";
	return 0;
}

5.1.4 最大生成树

有什么好说的呢…算法相同，其实就只把排序/比较大小反过来罢了。

大概就是这样。

5.2 次小生成树

分为 非严格次小生成树 和 严格最小生成树。差别其实就是是否有边权和 严格大于 MST 边权和。

简单来说，在找到 MST 后枚举未在 $E_{MST}$ 中的边 $u \to v$，然后断开 $u$ 到 $v$ 的路径上的最长边，将当前边加入边集，寻找最小的边权和即可。对于严格最小生成树，考虑到最长边边权可能与当前边权相同，还要同时记录 次大值。

严格最小生成树的伪代码如下：

\[\begin{array}{ll} 1 & \textbf{Input. } \text{The number of vertexs and edges of the undigraph } G, \\ & \text{the edges of the graph } e, \text{which element in } e \text{ is } (u,v,w) \\ & \text{denoting that there is an edge between } u \text{ and } v \text{ weighted } w . \\ 2 & \textbf{Output. } \text{The sum of the weights of the edges in the set of edges } E_{S}.\\ & \text{Or formally, } \sum_{e \in E_{S}} w_e.\\ 3 & \textbf{Method. }\\ 4 & \text{initialize the disjoint set union} \\ 5 & mstlen \gets 0,E_M \gets \varnothing \\ 6 & \text{sort } e \text{ into nondecreasing order by weight } w \\ 7 & \textbf{for } \text{each } (u,v,w) \text{ ordered } i \text{ in the sorted } e\\ 8 & \qquad \textbf{if } u \text{ and } v \text{ are not connected in the disjoint set union } \\ 9 & \qquad \qquad mstlen \gets mstlen + w\\ 10 & \qquad \qquad \text{merge } u \text{ and } v \text{ in the disjoint set union}\\ 11 & \qquad \qquad E_M \gets E_M \bigcup \{(u,v,w)\} \\ 12 & dfs(u \gets 1,fa \gets 0) \text{ to initialize the binary-lifting funtions} \\ 13 & ans \gets \infty \\ 14 & \textbf{for } \text{each } (u,v,w) \not \in E_M \text{ which satisfies } u \neq v \\ 15 & \qquad lca \gets \operatorname{LCA}(u,v),tmp_1 \gets - \infty, tmp_2 \gets - \infty \\ 16 & \qquad tmp_1 \gets \text{the maximum weight on the path from } lca \text{ to } u \\ 17 & \qquad \textbf{if } tmp_1 = w \\ 18 & \qquad \qquad tmp_1 \gets \text{the sub-maximum weight on the path from } lca \text{ to } u \\ 19 & \qquad tmp_2 \gets \text{the maximum weight on the path from } lca \text{ to } v \\ 20 & \qquad \textbf{if } tmp_2 = w \\ 21 & \qquad \qquad tmp_2 \gets \text{the sub-maximum weight on the path from } lca \text{ to } v \\ 22 & \qquad \textbf{if } tmp_1 = tmp_2 = - \infty \\ 23 & \qquad \qquad \textbf{continue} \\ 24 & \qquad ans \gets \min \left( ans, mstlen- \max(tmp_1,tmp_2)+w \right) \\ 25 & \textbf{return }ans \end{array} \]

放一段优美的 $code$：

#include<bits/stdc++.h>
#define ll long long
#define ld long double
#define forE(u) for(int p=head[u],v=E[p].to;p;p=E[p].next,v=E[p].to)
const int N=1e5+5,M=3e5+5;
const ll inf=1e18+9;
int n,m;
// set of edges module
bool used[M];
struct pr { int from,to; ll w; } prE[M];
inline void add(int u,int v,ll w,int id) { prE[id].from=u,prE[id].to=v,prE[id].w=w; }
int cnt,head[N];
struct edge { int to,next; ll w; } E[N<<1];
inline void addedge(int u,int v,ll w) { E[++cnt].to=v,E[cnt].w=w,E[cnt].next=head[u],head[u]=cnt; }
// DSU module
int fa[N];
void init() { for(int i=1;i<=n;++i) fa[i]=i; }
int get(int x) { return fa[x]==x?x:fa[x]=get(fa[x]); }
void merge(int x,int y) { fa[get(y)]=get(x); }
// kruskal module
ll kruskal() {
	init();
	std::sort(prE+1,prE+m+1,[](const pr &a,const pr &b){ return a.w<b.w; });
	int tot=0; ll ans=0; pr *it=prE;
	while(tot<n-1) {
		it++; if(it==prE+m+1) break;
		if(get(it->from)==get(it->to)) continue;
		ans+=it->w,used[it-prE]=1,merge(it->from,it->to),tot++;
		addedge(it->from,it->to,it->w),addedge(it->to,it->from,it->w);
	}
	return ans;
}
// MST module
int dep[N],anc[22][N];
ll mx[22][N],sec[22][N];
void dfs(int u,int f) {
	dep[u]=dep[f]+1,anc[0][u]=f,sec[0][u]=-inf;
	for(int i=1;(1<<i)<=dep[u];++i) {
		anc[i][u]=anc[i-1][anc[i-1][u]];
		ll tmp[]={mx[i-1][u],mx[i-1][anc[i-1][u]],sec[i-1][u],sec[i-1][anc[i-1][u]]};
		std::sort(tmp,tmp+4);
		mx[i][u]=tmp[3];
		int ptr=2;
		while(~ptr && tmp[ptr]==tmp[3]) ptr--;
		sec[i][u]=~ptr?tmp[ptr]:-inf;
	}
	forE(u) if(v!=f) mx[0][v]=E[p].w,dfs(v,u);
}
int LCA(int u,int v) {
	if(dep[v]>dep[u]) std::swap(u,v);
	int d=dep[u]-dep[v];
	for(int i=20;~i;--i) if(d&(1<<i)) u=anc[i][u];
	if(u==v) return u;
	for(int i=20;~i;--i) if(anc[i][u]!=anc[i][v]) u=anc[i][u],v=anc[i][v];
	return anc[0][u];
}
ll query(int u,int v,ll w) {
	ll ans=-inf;
	if(dep[v]>dep[u]) std::swap(u,v);
	int d=dep[u]-dep[v];
	for(int i=20;~i;--i) if(d&(1<<i)) {
		if(mx[i][u]==w) ans=std::max(ans,sec[i][u]);
		else ans=std::max(ans,mx[i][u]);
		u=anc[i][u];
	}
	return ans;
}
// beautiful main program
int main() {
	std::ios::sync_with_stdio(false);
	std::cin.tie(nullptr); std::cout.tie(nullptr);
	std::cin>>n>>m;
	for(int i=1,u,v,w;i<=m;++i) { std::cin>>u>>v>>w; add(u,v,w,i); }
	ll mstlen=kruskal(),ans=inf; dfs(1,0);
	for(int i=1;i<=m;++i) {
		if(used[i] || prE[i].from==prE[i].to) continue;
		int lca=LCA(prE[i].from,prE[i].to);
		ll tmp1=query(prE[i].from,lca,prE[i].w),tmp2=query(prE[i].to,lca,prE[i].w);
		if(tmp1==-inf && tmp2==-inf) continue;
		ans=std::min(ans,mstlen-std::max(tmp1,tmp2)+prE[i].w);
	}
	std::cout<<ans<<'\n';
	return 0;
}

posted @ 2023-05-10 19:55 二两碘酊阅读(51) 评论(0) 编辑收藏举报

刷新页面返回顶部

变量名	意义
\(mx\)	染色该点的最大点权
\(mn\)	染色该点的最小点权
\(maxcost\)	染色该点的最大点权差
\(mincost\)	到达该点时出现的最小点权
\(dp\)	到达该点的所有路径中的最大点权差

Michael Wong - 二两碘酊

从 LaTeX 到 C++，从平面设计与摄影构图到视频剪辑与电影艺术，钟爱各类视听逻辑美学与计算机艺术的热血高中少年

图论相关

CHANGE LOG

0. 写在前面

1. 基本概念

1.1 无向图

1.2 有向图

2. 拓扑排序 - TopoSort

2.1 引入

2.2 概念

2.2.1 AOV 网

2.2.2 定义与作用

2.2.3 不唯一性

2.3 实践

2.3.1 基础实现

2.3.2 其他方式

2.3.3 判断重边

2.4 练习

2.4.1 模板题

2.4.2 换个方式存图

2.4.3 抓住 Toposort 的特点

2.4.4 Topo 全排列

2.4.5 拓上 DP（doge）

2.4.6 绕个小弯

2.4.7 CCF 荣誉出品「君のNOIP」

2.5 其他运用

2.5.1 树上差分

2.5.2 博弈论

3. Tarjan 连通分量算法

3.1 理论基础

3.1.1 DFS 生成树

3.1.2 时间戳与追溯值

3.2 求有向图的强连通分量

3.2.1 逻辑梳理

3.2.2 代码实现

3.2.3练习

3.2.3.1 P2341 [USACO03FALL / HAOI2006] 受欢迎的牛 G

3.2.3.2 P1073 [NOIP2009 提高组] 最优贸易

3.2.3.3 P2863 [USACO06JAN]The Cow Prom S

3.3 求无向图的割点与桥

3.3.1 割点

3.3.2 桥

3.3.3 练习

3.3.3.1 模板题

3.3.3.2 POJ-1144 Network

3.3.3.3 P3469 [POI2008]BLO-Blockade

3.3.3.4 POJ-3352 Road Construction

3.4 求无向图的点/边双连通分量

3.4.1 v-DCC

3.4.1.1 逻辑梳理

3.4.1.2 代码实现

3.4.2 e-DCC

3.4.2.1 逻辑梳理

3.4.2.2 代码实现

4. 最短路

4.1 三角形不等式

4.2 单源最短路径

4.2.1 Bellman-Ford

4.2.2 SPFA

*最后的用武之地 - 判断负环

\(\textbf{SPFA}\) - OI 迅

4.2.3 Dijkstra

4.3 多源最短路径 - Floyd

5. 生成树

5.1 最小生成树 - MST

5.1.1 性质

5.1.2 Prim

5.1.3 Kruskal

5.1.4 最大生成树

5.2 次小生成树

公告