网络流入门手册

0. 前言

由于网络流极其庞大而资料有限，我决定用这个博客先记录一下我学习的大纲，在后期有可能补上内容。对于网上可以找到的，我就一笔带过，只是说明应该了解这个东西；而对于网上难以找到的一些资料，我会尽我所能写出来。

还介绍了一部分二分图和图的匹配，但是如题，我只介绍他们与网络流相关的部分知识。

推荐阅读 魏老师的博客 和 OI-wiki.

1. 理论与模板

1.1 基本概念

1.2 网络最大流 - 增广路类

• 最大流最小割定理：内容与证明
• Ford - Fulkerson 增广：以下所有算法的基础，从贪心上简单地 支持反悔 的实现（增加反边容量）
• Edmonds - Karp（\(O(nm^2)\)）：从 F-F 到 EK 的优化，最短路不减 引理（BFS 寻找最短增广路）
• dinic（\(O(n^2 m)\)）：当前弧优化，整体 增广过程 的把握（多路增广）
• ISAP：单次 BFS 与 GAP（尤其是实现时 if(!ans) return flow; 阻止优化后的 dep 修改机制影响正确性）
• F-F \(\to\) EK \(\to\) dinic \(\to\) ISAP，其实是一个不断迭代优化的过程，贪心反悔贯穿始终。
• 时间复杂度证明：反证法 和 极限思想 的极致体现

1.2.1 dinic 复杂度证明

OI-wiki 和 知乎 都给出了证明方法。这里给出一种在 catandcode 的证明基础上在语言表述方面做了一些修改的版本。

定理 1.　使用当前弧优化的 Dinic 算法的时间复杂度为 \(O(|V|^2 |E|).\)

要证明这个定理，我们考虑分为两个步骤。

引理 2.　Dinic 进行单次多路增广的时间复杂度为 \(O(|V||E|).\)

设当前层次图为 \(G_L=(V,E_L).\)

考虑单次增广时的每条增广路，它们都是在 \(G_L\) 上沿当前弧跳转的结果，每一条增广路的跳转次数不可能超过 \(|V|.\)

在单次增广中，所有满流边组成的边集 \(E_1\) 与不满流或找不到增广路的边组成的边集 \(E_2\) 不交，且两者的并 \((E_1 \cup E_2) \subset E_L ,\) 故单次增广的总跳转次数不超过 \(|V||E_L|.\) 该引理得证。

接下来，我们需要证明 Dinic 的增广轮数不可能超过 \(|V|,\) 我们需要证明下面的引理。

引理 3.　Dinic 的每一代层次图的层数严格单调递增。

这是 Dinic 复杂度证明中最重要的部分。首先，回顾一下证明 EK 复杂度时提出的 最短路不减 引理，我们之后还会用到。

引理 4.　每次增广后，残量网络上 \(S\) 到每个节点的最短路长度不减。

这个引理我们不再证明。由于 dinic 是在 EK 的基础上添加了多路增广和层次图机制，所以 EK 的最短路不减引理在 dinic 中 仍然成立。

我们设在当前残量网络 \(G_f=(V,E_f)\) 上 \(S\) 到 \(u\) 的最短路长度为 \(dis_u,\) 则

\[\forall (u,v) \in E_f, \ dis_u +1 \geq dis_v. \]

在 dinic 中，\(dis_u\) 的意义也就是在对残量网络 \(G_f\) 以源点 \(S\) 建立的层次图 \(G_L=(V,E_L)\) 上，\(u\) 的层数。

接下来考虑使用反证法证明引理 3. 假设某次增广后的新一代层次图 \(G'_L=(V,E'_L)\) 与上一代层次图 \(G_L=(V,E_L)\) 的层数相同，则意味着两代层次图上 \(T\) 的层数相同，即 \(dis'_T = dis_T.\)

设增广后的残量网络上 \(S\) 到 \(T\) 的增广路最短路为 \(P',\) 则

\[\forall (u,v) \in P', \ dis'_v = dis'_u + 1. \]

我们断言 \(P'\) 与上一代层次图中的最短路 \(P\) 相比，必然存在一条边 \((u,v) \not \in E_L ,\) 否则 \(P'\) 就应该在 \(G_L\) 而非 \(G'_L\) 上被增广。

令 \((u,v)\) 是满足断言的那条边，其满足断言的原因只能是以下二者之一。

• \((u,v) \in E_f,\) 则该边在上次增广后加入到层次图中，那么必然有 $dis_u +1 > dis_v, $ 而本轮中 \(dis'_u +1 = dis'_v,\) 根据最短路不减引理，必然是 \(v\) 的最短路长度增加。设增广前后路径 \(v \to T\) 上的节点数分别为 $d,\ d', $ 则

  \[dis'_u \geq dis_u,\ d' \geq d,\ dis'_v = dis'u + 1 \geq dis_u +1 > dis_v \implies dis'_T = dis'_v + d' > dis_v + d. \]

• \((u,v) \not \in E_f,\) 则该边是上次增广后退流产生的反边，那么必然有 \(dis_u = dis_v +1,\) 根据最短路不减引理，\(dis'_v \geq dis_v+2,\) 则

  \[dis'_T = dis'_v + d' \geq dis_v +2 + d = dis_T +2 \]

可见，以何种方式满足断言均有 $dis'_T > dis_T, $ 这与反证假设 $dis'_T = dis_T $ 冲突，引理 3 得证。

由引理 3 可得，Dinic 的增广轮数是 \(O(|V|)\) 的。结合引理 2, 我们将单轮增广的时间复杂度 \(O(|V||E|)\) 与增广轮数 \(O(|V|)\) 相乘，可得 Dinic 算法的时间复杂度是 \(O(|V|^2|E|).\) 定理 1 得证。

\[\textbf{Q.E.D.} \]

1.2.2 关于 ISAP 你需要的

1.2.2.1 代码

OI-wiki 的代码好像有问题，此外他本身也比较复杂，可以考虑使用如下代码。

$\text{ AC Code by ISAP with the current arc, gap and dep optimization, } 46 ms\text{ with O2.}$

#include<bits/stdc++.h>
#define ll long long
#define ld long double
#define fsp(x) std::fixed<<std::setprecision(x)
#define forE(u) for(int p=head[u],v=to[p];p;p=next[p],v=to[p])
const int N=205,M=5005;
struct network {
	int cnt=1,head[N],to[M<<1],next[M<<1];
	ll lim[M<<1];
	inline void add(int u,int v,ll w) {
		to[++cnt]=v,lim[cnt]=w,next[cnt]=head[u],head[u]=cnt;
		to[++cnt]=u,lim[cnt]=0,next[cnt]=head[v],head[v]=cnt;
	}
	int n,s,t,cur[N],dis[N],gap[N];
	ll dfs(int u,ll res) {
		if(u==t) return res;
		ll flow=0;
		for(int &p=cur[u];p&&res;p=next[p]) {
			int c=std::min(res,lim[p]),v=to[p];
			if(dis[u]==dis[v]+1&&c) { ll fl=dfs(v,c); flow+=fl,res-=fl,lim[p^1]+=fl,lim[p]-=fl; }
			if(!res) return flow;
		}
		if(--gap[dis[u]]==0) dis[s]=n;
		return ++gap[++dis[u]],flow;
	}
	ll maxflow(int n,int s,int t) {
		ll flow=0; std::queue<int> q;
		this->n=n,this->s=s,this->t=t;
		memset(dis,0x3f,sizeof dis);
		memset(gap,0,sizeof gap);
		++gap[dis[t]=0],q.push(t);
		while(!q.empty()) {
			int u=q.front(); q.pop();
			forE(u) if(dis[v]==0x3f3f3f3f&&!lim[p]) ++gap[dis[v]=dis[u]+1],q.push(v);
		}
		while(dis[s]<n) { memcpy(cur,head,sizeof head); flow+=dfs(s,1e18); }
		return flow;
	}
} f;
int n,m,s,t;
int main() {
	std::ios::sync_with_stdio(false);
	std::cin.tie(nullptr); std::cout.tie(nullptr);
	std::cin>>n>>m>>s>>t;
	for(int i=1,u,v,w;i<=m;++i) { std::cin>>u>>v>>w; f.add(u,v,w); }
	std::cout<<f.maxflow(n,s,t)<<'\n';
	return 0;
}

维护 ISAP 中的 \(dep,\) 必须是在 BFS 中使用 dep[v]=dep[u]+1, 判断时使用 dep[v]==dep[u]-1, + - 号 不能弄反！部分图可以过，可但凡强一点就过不去了，平时检查还检查不出来，这个地方务必注意！！！

UPD. 2023.9.3：

ISAP 最好 dis 要 memset 成 0x3f！ 可能会有一些情况比如 dis[s]=-1 了还在流，比如 星际转移问题 改成 0x3f 就快到飞起，不改就是 TLE。

再介绍一个节省时间的方法，如果你需要 多次增广，而前几次 远达不到 你数组开的上界，这种情况下优化会更加明显。就是你可以 把 memset 的 size 改成 sizeof(int)*n，这样会比全 memset 快一点。但注意，这样的提升其实是 有限 的。

1.2.2.2 优化后的 ISAP 深度维护机制正确性证明

developed by. cat_and_code & MichaelWong, 试证明 ++gap[++dep[u]]; 的正确性。

考虑采用数学归纳法。首先，我们先了解该机制的运行细节。

引理 1.　在多路增广中，增广路中满流的边靠近源点一侧的节点 \(u\) 到源点 \(T\) 的路径上的所有节点深度不改变。

考虑我们多路增广的过程 ll dfs(int u,ll ans)，dfs 的第二个传参 ans 表示阻塞流大小。所以从 \(u\) 到 \(T\) 的路径的 \(ans\) 必然被流光，即 \(ans=0.\) 根据 if(!ans) return flow; 必然直接返回，不改变深度。该引理得证。

接下来，我们分情况证明其正确性。

结论 2.　对于再无法提供贡献的节点，深度逐渐增加，且其效果与深度赋值极大值等效。

考虑为无法贡献节点赋值极大值（一般是 \(n\)）的目的：使其无法再提供贡献。深度增加会使这些节点组成路径最终与汇点无法通过判断语句 dep[v]==dep[u]-1，遍历至汇点，故深度增加与深度赋值极大值等效。但是，这种写法会导致这些节点在接下来的遍历过程中仍然被访问，经历多次 dfs 空轮，（但无法抵达 \(T\)，没有贡献，）深度仍会逐渐增加，至此该结论得证。这有可能增加运算量，但整体影响不大，同时为接下来的证明做了保证。该深度维护机制在整体上对代码书写与运行速度的提升都是正向的。

结论 3.　对于还能继续产生贡献的节点，深度增加可以保证其所有边的贡献全部被计入。

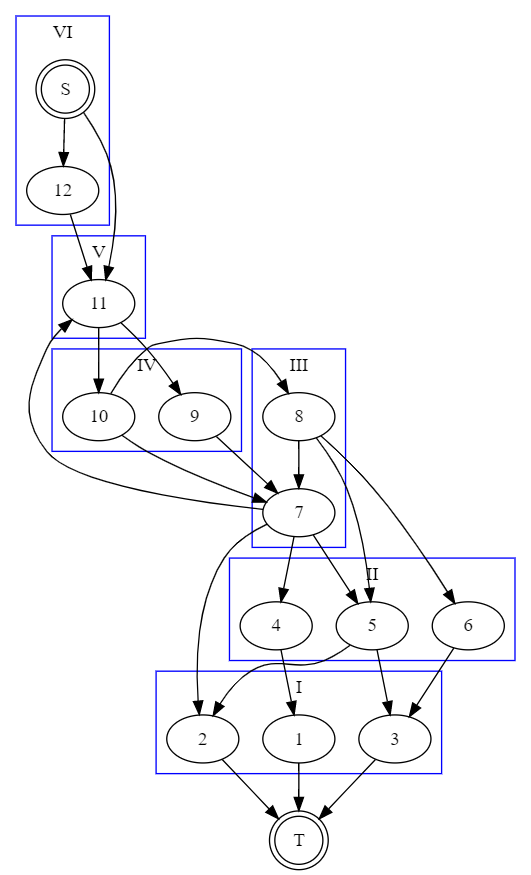
我们以汇点 \(T\) 为中心建立层次图，\(dis(u)\) 表示节点 \(u\) 的层次，将 所有非满流边（包括反边） 大致分为以下几类：（名称是根据增广时的上下关系，自己取的。）

• 上溯边：前往 \(dis(u)<=dis(v)\) 的节点 \(v\) 的边，如图中 \((11,7),(7,8)\)；（即 \(u\) 更靠近 \(T\) 一侧）
• 合法边：前往 \(dis(u)=dis(v)+1\) 的节点 \(v\) 的边，如图中 \((7,9)\)；（当前层次图要走的边）
• 下越边：前往 \(dis(u)>dis(v)+1\) 的节点 \(v\) 的边，如图中 \((2,7)\)。（即 \(v\) 更靠近 \(T\) 一侧，但是 \(u,v\) 跨度不止一层）

接下来我们分别证明这些边的贡献会被计入。

• 上溯边：我们把所有上溯边抽象成如下模型：

  

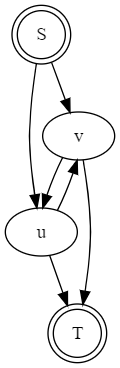
  省略了 \(S \to u, S \to v, u \to T, v \to T\) 的若干边，\(dis(u),dis(v)\) 不一定相同。其中 \((u,v)\) 是上溯边。

  考虑增广后在残量网络中消失的边的所有位置，会对该上溯边如下结果：

  • 边消失后，可达性不变或 \(v\) 不可达 \(u\)：对该上溯边无影响；
  • 边消失后，\(S\) 不可达 \(v\)：除经过该上溯边外，无法遍历至 \(v,\ v\) 深度不变。
  • 边消失后，\(S\) 不可达 \(u\) 或 \(v\) 不可达 \(T\)：该上溯边 不可能 再提供贡献。
  • 边消失后，\(u\) 不可达 \(T\)：此后 \(u\) 无法提供贡献。根据结论 2，\(u\) 的深度将在多次 dfs 空轮中逐渐增加。

  至此易得，要么该上溯边 不可能 再提供贡献，要么在 \(S\) 不可达 \(v,\ u\) 不可达 \(T\) 后，\(v\) 深度不变，\(u\) 深度逐渐增加，必然有 \(dis(u)=dis(v)+1,\) 成为合法边。

• 合法边：若此次阻塞流不在边 \((u,v)\) 上，则 \(u,v\) 的深度同时增加，该边仍然合法，有机会在后续的遍历中继续被增广。

• 下越边：考虑下越边的定义，\(dis(u)\) 必然曾经定义为 \(dis(v)+1.\) 故如果这个边 不是反边，则其贡献必然 已经被计入，随后因为 满流 等原因导致 \(u\) 的深度增加而 \(v\) 不变；若其 是反边，则其应该为 上溯边 的反边（准确来说是 返祖边，即前往 \(dis(u)<dis(v)\) 的节点 \(v\) 的边），考虑该返祖边贡献被计入的时刻。当时此返祖边为合法边，而该边是 返祖边，故贡献也可在作为返祖边时被计入。

综上，所有类型边的贡献均被计入，该结论得证。

根据结论 2 和结论 3，当前深度维护机制的正确性得以证明。

1.3 网络最大流 - 预留推进类

准备鸽了……OI中用处不大，学完其他的再学 qwq

1.4 无负环费用流

• 基于 EK 的 SSP：如何 结合 EK 和 SPFA，正确性证明
• 基于 dinic 的 SSP：如何 写出正确的代码，注意 dfs 错误可能导致 爆栈空间
• Primal-Dual 原始对偶：类似 Johnson 的方法给节点赋势能调整边权，然后跑 Dijkstra.

魏老师没有给出 dinic 的 SSP 代码，这里我给一个我的版本。

$\text{ AC Code by SSP based on dinic with the current arc optimization, } 1.29s \text{ without O2.}$

#include<bits/stdc++.h>
#define ll long long
#define ld long double
#define pii std::pair<int,int>
#define fsp(x) std::fixed<<std::setprecision(x)
#define forE(u) for(int p=head[u],v=to[p];p;p=next[p],v=to[p])
const int N=5e3+3,M=5e4+4;
struct network {
	int cnt=1,head[N],to[M<<1],lim[M<<1],cst[M<<1],next[M<<1];
	inline void add(int u,int v,int w,int c) {
		to[++cnt]=v,lim[cnt]=w,cst[cnt]=c,next[cnt]=head[u],head[u]=cnt;
		to[++cnt]=u,lim[cnt]=0,cst[cnt]=-c,next[cnt]=head[v],head[v]=cnt;
	}
	int t,cost,dis[N],cur[N],in[N];
	int dfs(int u,int res) {
		if(u==t) return res;
		int flow=0; in[u]=1;
		for(int p=cur[u];p&&res;p=next[p]) {
			int c=std::min(res,lim[p]),v=to[p]; cur[u]=p;
			if(dis[v]==dis[u]+cst[p]&&c&&!in[v]) { int fl=dfs(v,c); flow+=fl,res-=fl,lim[p^1]+=fl,lim[p]-=fl,cost+=cst[p]*fl; }
		}
		if(!flow) dis[u]=0x3f3f3f3f;
		return in[u]=0,flow;
	}
	pii mincost(int s,int t) {
		int flow=0; cost=0,this->t=t;
		while(1) {
			std::queue<int> q;
			memset(dis,0x3f,sizeof dis);
			dis[s]=0,q.push(s);
			while(!q.empty()) {
				int u=q.front(); in[u]=0,q.pop();
				forE(u) if(lim[p]&&dis[v]>dis[u]+cst[p]) dis[v]=dis[u]+cst[p],!in[v]&&(q.push(v),in[v]=1);
			}
			if(dis[t]>1e9) return {flow,cost};
			memcpy(cur,head,sizeof head),flow+=dfs(s,1e9);
		}
	}
} f;
int n,m,s,t;
int main() {
	std::ios::sync_with_stdio(false);
	std::cin.tie(nullptr); std::cout.tie(nullptr);
	std::cin>>n>>m>>s>>t;
	for(int i=1,u,v,w,c;i<=m;++i) { std::cin>>u>>v>>w>>c; ntw.add(u,v,w,c); }
	auto ret=ntw.mincost(s,t);
	std::cout<<ret.first<<' '<<ret.second<<'\n';
	return 0;
}

1.4.1 关于原始对偶

好像大部分原始对偶都是用 EK, 也确实挺快的。（甚至开 O2 比 dinic 的还快？虽然不开 O2 他会 T 一个。）

$\text{ AC Code by Primal-Dual based on EK, } 597ms \text{ with O2.}$

#include<bits/stdc++.h>
#define ll long long
#define ld long double
#define pii std::pair<int,int>
#define fsp(x) std::fixed<<std::setprecision(x)
#define forE(u) for(int p=head[u];p;p=next[p])
const int N=5e3+3,M=5e4+4,inf=0x3f3f3f3f;
int n,m,s,t;
struct network {
	int cnt=1,head[N],to[M<<1],next[M<<1],lim[M<<1],cst[M<<1];
	inline void add(int u,int v,int w,int c) {
		to[++cnt]=v,lim[cnt]=w,cst[cnt]=c,next[cnt]=head[u],head[u]=cnt;
		to[++cnt]=u,lim[cnt]=0,cst[cnt]=-c,next[cnt]=head[v],head[v]=cnt;
	}
	int cost,h[N],in[N],dis[N];
	inline void SPFA() {
		for(int i=1;i<=n;++i) h[i]=inf;
		std::queue<int> q;
		h[s]=0,q.push(s);
		while(!q.empty()) {
			int u=q.front(); in[u]=0,q.pop();
			forE(u) { int v=to[p]; if(h[u]+cst[p]<h[v] && lim[p]) { h[v]=h[u]+cst[p]; if(!in[v]) in[v]=1,q.push(v); } }
		}
	}
	int fl[N],from[N];
	pii mincost() {
		SPFA();
		int flow=0; cost=0;
		while(1) {
			std::priority_queue<pii> q;
			for(int i=1;i<=n;++i) dis[i]=inf,in[i]=0;
			fl[s]=inf,dis[s]=0,q.push({0,s});
			while(!q.empty()) {
				int u=q.top().second; q.pop();
				if(in[u]) continue; in[u]=1;
				forE(u) {
					if(!lim[p]) continue;
					int v=to[p],w=cst[p]+h[u]-h[v];
					if(dis[u]+w<dis[v]) fl[v]=std::min(fl[u],lim[p]),from[v]=p,dis[v]=dis[u]+w,q.push({-dis[v],v});
				}
			}
			if(dis[t]>=inf) return {flow,cost};
			for(int i=t;i!=s;i=to[from[i]^1]) lim[from[i]]-=fl[t],lim[from[i]^1]+=fl[t];
			for(int i=1;i<=n;++i) h[i]+=dis[i];
			flow+=fl[t],cost+=h[t]*fl[t];
		}
	}
} f;
int main() {
	std::ios::sync_with_stdio(false);
	std::cin.tie(nullptr); std::cout.tie(nullptr);
	std::cin>>n>>m>>s>>t;
	for(int i=1,u,v,w,c;i<=m;++i) { std::cin>>u>>v>>w>>c; f.add(u,v,w,c); }
	pii ret=f.mincost();
	std::cout<<ret.first<<' '<<ret.second<<'\n';
	return 0;
}

然后是 dinic, 刚开始多路增广不会更新 \(dis,\) 所以把 Dijksrta 退化成了堆优化的 Bellman - Ford. 不过这意味着刚开始的 SP 白用了，而且这说白了就是一个 SSP 而不是原始对偶了。且不开 O2 会 T 一个。
后来恍然大明白，改过来了。但是刚开始的时候我出现了这么一个离谱的现象 hhhh

上午 \(\to\) 中午：

\(\to\)

不过后来发现是刚开始的 #define int ll 忘删了，拖我尾速了。现在没问题了，不吸氧都能过的优秀。下来展示我真正的 Primal-Dual.

$\text{ AC Code by Primal-Dual based on dinic with Dijkstra, } 2.14s \text{ without O2, } 605ms \text{ with O2.}$

#include<bits/stdc++.h>
#define ll long long
#define ld long double
#define pii std::pair<int,int>
#define fsp(x) std::fixed<<std::setprecision(x)
#define forE(u) for(int p=head[u];p;p=next[p])
const int N=5e3+3,M=5e4+4;
int n,m,s,t;
struct network {
	int cnt=1,head[N],to[M<<1],next[M<<1],lim[M<<1],cst[M<<1];
	inline void add(int u,int v,int w,int c) {
		to[++cnt]=v,lim[cnt]=w,cst[cnt]=c,next[cnt]=head[u],head[u]=cnt;
		to[++cnt]=u,lim[cnt]=0,cst[cnt]=-c,next[cnt]=head[v],head[v]=cnt;
	}
	int cost,h[N],in[N],dis[N],cur[N];
	inline void SPFA() {
		for(int i=1;i<=n;++i) h[i]=0x3f3f3f3f;
		std::queue<int> q;
		h[s]=0,q.push(s);
		while(!q.empty()) {
			int u=q.front(); in[u]=0,q.pop();
			forE(u) { int v=to[p]; if(h[u]+cst[p]<h[v] && lim[p]) { h[v]=h[u]+cst[p]; if(!in[v]) in[v]=1,q.push(v); } }
		}
	}
	int dfs(int u,int res) {
		if(u==t) return res;
		int flow=0; in[u]=0;
		for(int p=cur[u];p&&res;p=next[p]) {
			if(!lim[p]) continue; cur[u]=p;
			int c=std::min(lim[p],res),v=to[p],w=cst[p]+h[u]-h[v];
			if(dis[u]+w==dis[v]&&in[v]) { int fl=dfs(v,c); flow+=fl,res-=fl,lim[p]-=fl,lim[p^1]+=fl,cost+=cst[p]*fl; }
		}
		return in[u]=1,flow;
	}
	pii mincost() {
		SPFA();
		int flow=0; cost=0;
		while(1) {
			std::priority_queue<pii> q;
			for(int i=1;i<=n;++i) dis[i]=0x3f3f3f3f,in[i]=0,cur[i]=head[i];
			dis[s]=0,q.push({0,s});
			while(!q.empty()) {
				int u=q.top().second; q.pop();
				if(in[u]) continue; in[u]=1;
				forE(u) {
					if(!lim[p]) continue;
					int v=to[p],w=cst[p]+h[u]-h[v];
					if(dis[u]+w<dis[v]) dis[v]=dis[u]+w,q.push({-dis[v],v});
				}
			}
			if(dis[t]>1e9) return {flow,cost};
			flow+=dfs(s,1e9);
			for(int i=1;i<=n;++i) h[i]+=dis[i];
		}
	}
} f;
int main() {
	std::ios::sync_with_stdio(false);
	std::cin.tie(nullptr); std::cout.tie(nullptr);
	std::cin>>n>>m>>s>>t;
	for(int i=1,u,v,w,c;i<=m;++i) { std::cin>>u>>v>>w>>c; f.add(u,v,w,c); }
	pii ret=f.mincost();
	std::cout<<ret.first<<' '<<ret.second<<'\n';
	return 0;
}

P.S. 但是好像没有 SSP 快？魏子曰：

实际表现方面，Primal-Dual 相较于 SSP 并没有很大的优势，大概是因为 SPFA 本身已经够快了，且堆优化的 dijkstra 常数较大。

所以我觉得考场上我还是会写 SSP. 但是原始对偶确实在开 O2 的情况下跑得飞快。

1.5 上下界网络流

• 无源汇可行流：实现原理（魏老师说新图结构体要开外面，但是我开里面也过了 qwq）
• 有源汇可行流：到无源汇可行流的转换
• 有源汇最大流：在可行流的基础上添砖加瓦
• 有源汇最小流：+ \(\to\) - \(\text{and } {\color{Green}\text{AC}} .\)

上下界网络流 Libre OJ 比较全，然后这里是我的 无源汇可行流、有源汇最大流、有源汇最小流 代码。魏老师说 struct graph 要开外面但是我试了试开里面也没事所以我也不知道为什么 qwq, 但是开外面好像大数据更快？我不知道。

1.6 应用与模型

• 最小割 / 最小割点：\(i \to (i_{in},i_{out},w_i),\) 解决将后者转换为前者，然后求最大流即可。
• 集合划分：建图，一些特殊情况（负权，单向边等等）。
• 最大权闭合子图：负点权的处理。
• 有负环的费用流：强制负权边满流。
• 最大费用最大流：全部取相反数跑有负环的费用流。

2. 练习与经验

2.1 网络流在二分图上的应用

简记：

• 源点：\(S;\)
• 汇点：\(T;\)
• 左部点：\(V_1;\)
• 右部点：\(V_2;\)
• \(u\) 到 \(v\) 连 流量 为 \(w\) 的边：\(u \xrightarrow{w} v.\)

接下来是二分图的常见问题和一些常见的模型：

• 最大匹配：$\forall u \in V_1, \ S \xrightarrow{1} u ; \ \forall u \in V_2, \ u \xrightarrow{1} T ; \ \forall (u,v) \in E, \ u \xrightarrow{1} v . $ 跑最大流即可。

• 最大多重匹配：若每个点有连边限制 \(L_u,\) 只需 \(\forall u \in V_1, \ S \xrightarrow{L_u} u ; \ \forall u \in V_2, \ u \xrightarrow{L_u} T ,\) 其余和最大匹配相同，跑最大流即可。

• 带权最大匹配：最大流 \(\to\) 费用流，最大权最大匹配需将 边权取反，完美匹配交给 EK 算法。

• 最小点覆盖集：根据 König 定理，直接求最大匹配。

  König 定理：二分图的最大匹配大小等于最小点覆盖集大小。

  可以认为最小覆盖点集的求法源于 集合划分模型，具体做法与最大匹配相同。所以从这点来说，将其修改为带权最小点覆盖集也很简单，从集合划分模型考虑，只需将 \(S \to u\) 和 \(u \to T\) 的连边流量大小改为点权，\(\forall (u,v) \in E, \ u \xrightarrow{+ \infty} v\) 即可。

• 最大独立集：与最小点覆盖集 互为补集，故用 \(|V|\) 减去最小点覆盖集大小即可。

• 最大团：\(=\) 补图最大独立集。

• 某部点的极值：考虑利用集合划分模型，修改 \(S \to u\) 和 \(u \to T\) 的边权为 \(c\) 和 \(c+1,\) 强制优先断开某部点。其中 \(c\) 可证明应满足不小于 \(n=min(|V1|,|V2|).\)

• DAG 最小可交路径覆盖：相当于其传递闭包的最小不交路径覆盖

这里没有给出这些模型的解法证明，因为目前来讲这个手册只是一个大纲，但是仍然希望读者能够通过 魏老师的博客 阅读并理解这些模型为何和如何用网络流的知识得到解决。

2.2 网络流与线性规划 24 题

• 餐巾计划问题：刚开始建的图错了……所以建图的时候必须要考虑，你需要的答案就是 最小费用最大流。
• 星际转移问题：领略 分层图 的奥义。
• 飞行员配对方案问题：锻炼使用网络流解决 二分图的最大匹配。
• 软件补丁问题：状态压缩最短路，锻炼不建边与位运算。
• 太空飞行计划问题：了解 最大权闭合子图 的解决方法。
• 试题库问题：用建图 表达需求。
• 最小路径覆盖问题：了解诉求到 二分图的最大匹配 的转换。
• 魔术球问题：学习实际问题到 最小路径覆盖问题 的转换，以及其 正确性证明。

  Q: 为什么跑到 \(i+1\) 的最大流发现不可行后，\(i\) 作为正确答案时仍然可以用 \(i+1\) 跑最大流的图输出路径？
  A: 因为将隐式图转换成二分图进行匹配后，整个图只有四层：源点、左部点、右部点和汇点，且容量都是 \(1,\) 因此我们解决最小路径覆盖问题的底层思路是对每一条边单独判断是否在路径覆盖边集中，而不是匹配整个路径，所以在该图中不存在反悔的情况，每一次的结果都是在上一次的基础上做的添加，不会改变以前的结果。

• 最长不下降子序列问题：前 DP 后网络流，锻炼将问题 转换成最大流 的能力。
• 航空路线问题：练习利用 流量限制 结合 拆点 解决问题。
• 方格取数问题：二分图最大独立集，技巧是对于棋盘 黑白染色 建立二分图。
• 圆桌问题：二分图的多重匹配，个人认为很直观。
• 骑士共存问题：注意到限制都是在 两种颜色的格子之间，仍然黑白染色，更换限制条件即可。
• 火星探险问题：就是输出 dfs 的时候费点心思，感觉可以考察对 边与反边的流量等性质的认识 ？
• 最长 \(k\) 可重区间集问题：灵活建图，隐式图的转化。
• 最长 \(k\) 可重线段集问题：对 自环 的判断和解决方法。
• 汽车加油行驶问题：拆点最短路，最短路的经典变种。
• 孤岛营救问题：拆点 bfs，和汽车加油行驶问题搭配食用。
• 深海机器人问题：和火星探险问题很像，善用 平行边。
• 数字梯形问题：运用 拆点 满足限制，对 费用流性质 的把握（最大流不变的情况下，多次费用流不可加）。
• 分配问题：最大 / 最小二分图完美匹配。
• 运输问题：稍微有点灵活的 分配问题。
• 负载平衡问题：锻炼一下 问题转化能力？我的建图方法好像比魏老师还优 qwq.