关于数据结构

CHANGE LOG

  • 2023.2.14 修改 LCA 预处理部分代码。
  • 2023.2.19 修改 ST 表查询部分代码。
  • 2023.6.10 合并字典树部分进入博客，增加平衡树与线段树进阶。

写在前面

本文会梳理大部分初级的、和部分常用的进阶数据结构。部分内容由于时间较紧等到以后重构。

我们进入正题。

线段树

理论

线段树，顾名思义，我们将一个线段看作一个节点，由这样的无数个节点形成的树，我们称之为 线段树。线段树是常见的 维护区间信息 的数据结构。

直接给图：

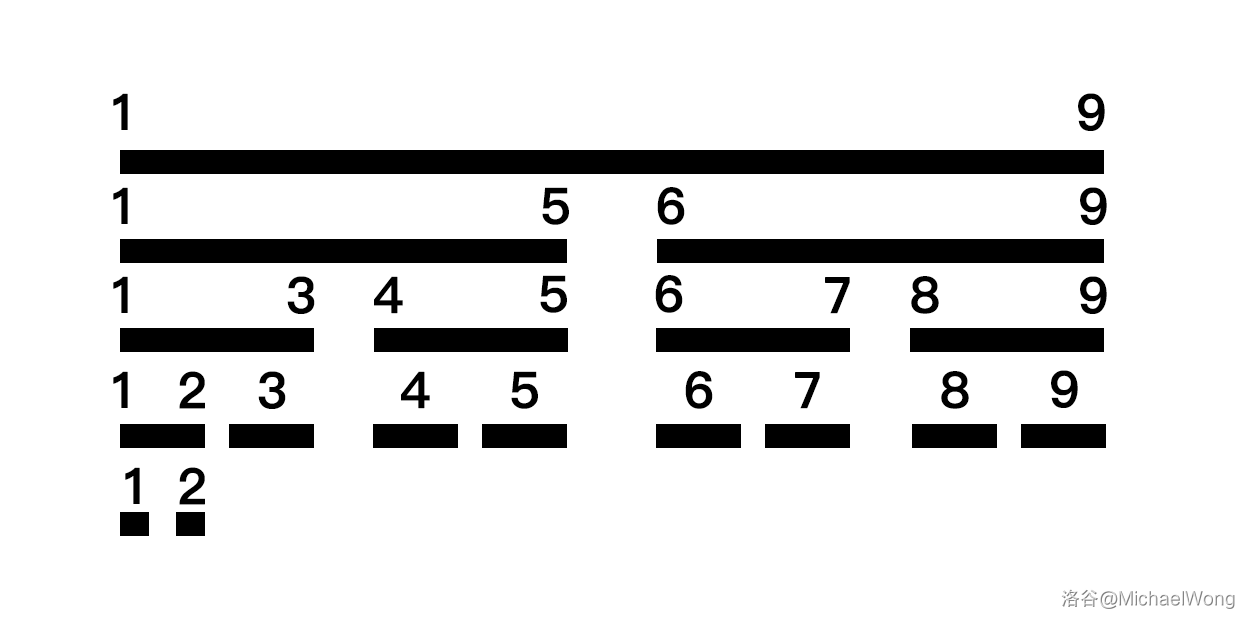
线段树图例

要维护区间 \([1,9]\)，生成的线段树就如上图所示。一般来讲，对于元素数量为 \(N\) 的区间，生成的线段树的节点数量 不会 超过 \(4N\) ，所以开数组时开到 4 倍即可。

基础线段树

我们结合 模板题：P3372 【模板】线段树 1 进行讲解。在这道题中，我们需要实现两种操作：

  • 区间加：给定 \(l\),\(r\),\(k\)，将 \([l,r]\) 中的所有元素加上 \(k\)。
  • 区间查询：给定 \(l\),\(r\),\(k\)，查询 \([l,r]\) 中所有元素的和。

线段树是一棵 二叉树。所以按照 BFS 序编号时，节点 \(x\) 的两个子节点分别为 \(2x\) 和 \(2x+1\)（即二进制下的 x>>1 和 x>>1|1），我们可以利用这个性质向下遍历。在书写中，为了方便，我们一般在缺省源中加入这两行：

#define ls x<<1
#define rs x<<1|1

接下来进入线段树的代码部分。

上传 - pushup

一般来讲，线段树上层节点信息的维护 极依赖其子节点，所以在每次修改子节点后，我们需要将两个子节点的信息上传到当前节点。如在这里，我们需要维护每个节点的区间和：

void pushup(int x) { sum[x]=sum[ls]+sum[rs]; }

建树 - build

我们采用 DFS 的方法建树，预处理每个节点所代表的区间内的所有元素的和 \(sum_x\)。

部分线段树写法会预处理每个节点代表的区间 $[L_x,R_x], $ 现在我 不建议这么做。因为在后期更复杂的操作中，这多出来的两个数组会占用空间，也会容易导致错误。

代码如下：

void build(int x,int l,int r) { //传参：节点编号，区间边界
	if(l==r) return sum[x]=a[l],void();
	int mid=l+r>>1;
	build(ls,l,mid),build(rs,mid+1,r);
	pushup(x);
}

区间修改（加） - change

大部分平衡树的基础操作，很多进阶题的基本组成部分。

要修改给定的区间 \([l,r]\) 内的所有元素，如果对所要求的区间 \([l,r]\) 中的所有节点都进行修改，时间复杂度无法承受。所以，在线段树中，我们引入了一个新的变量，巧妙的节约了时间，我们通常称这个变量为 懒标记，代码中常写作 lazy。

顾名思义，懒标记是一个非常 “ 懒 ” 的方法——我们用懒标记记录该节点所代表的区间里每一个元素改变的值，在修改一个区间时，我们只修改表示这个区间的节点，并为它打上懒标记，而不向下修改它的孩子们，这样极大地节省了时间。至于它的孩子们，当需要访问他们的时候，我们再将懒标记 下传。

有了懒标记，我们只需把要修改的区间拆成尽量少的多个区间，使得在线段树中存在若干个节点直接代表拆开后的区间，并对这些区间进行修改即可。

举个栗子，还是 \([1,9]\)，我们建好树后大概就是这个样子：

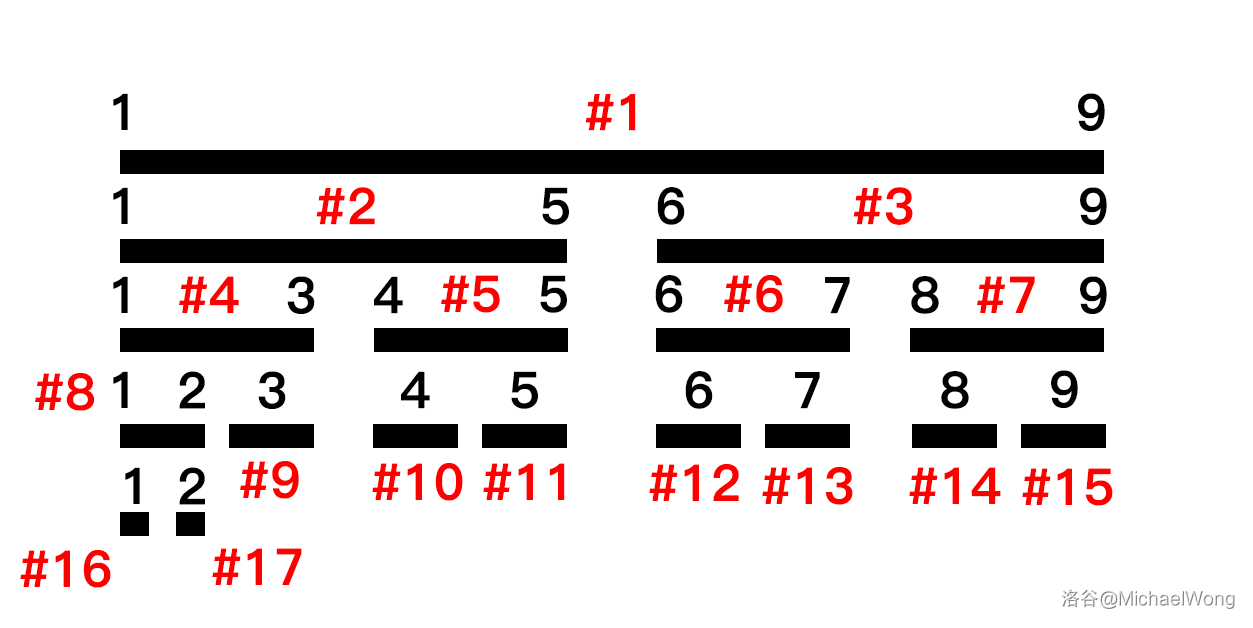
线段树标号

这里我们可以列举几种情况：

  • 如果我们要修改 \([1,9]\) ，就直接修改 \(sum_1\) 和 \(lazy_1\)；
  • 如果是修改 \([1,3]\)， 就可以通过二分找到 \(\#1 \to \#2 \to \#4\)，然后修改 \(sum_4\) 和 \(lazy_4\)；
  • 如果修改 \([5,8]\)，则需要拆成多个区间，节点分别为 \(\#11\)、\(\#6\)、\(\#14\) ，最后修改他们的 \(sum\) 和 \(lazy\)。

特别注意，当我们访问具有懒标记的节点的子节点时，要现将懒标记 下传 ，否则会影响结果。

代码：

void change(int x,int L,int R,int l,int r,int k) { //当前节点编号，当前所在区间，需要修改的区间，修改的值
	if(l<=L && r>=R) return sum[x]+=(R-L+1)*k,lazy[x]+=k,void(); //当前区间就是要修改的区间
	if(l>R || r<L) return; //当前区间与修改区间不重复
	pushdown(x,L,R); //懒标下传
	int M=L+R>>1;
	change(ls,L,M,l,r,k),change(rs,M+1,R,l,r,k); //修改子区间
	pushup(x); //上传
}

部分代码中会将修改部分写为：

if(r<=M)	change(ls,L,M,l,r,k);
else if(l>M)	change(rs,M+1,R,l,r,k);
else change(ls,L,M,l,M,k),change(rs,M+1,R,M+1,r,k);

这无疑是对的，但是会增加码量，同时对区间匹配错误的情况没有保护措施，容易产生 RE 或死循环，所以 不建议这么写。

懒标下传 - pushdown

刚才我们已经介绍了懒标记，简单来说，懒标记帮我们把多次操作记录下来，在向下访问的时候一起下传修改。所以，懒标下传至关重要。

因为非常简单，我就直接上代码了：

void pushdown(int x,int l,int r) //将x节点的懒标记下传
{
	int mid=l+r>>1;
	sum[ls]+=(mid-l+1)*lazy[x],sum[rs]+=(r-mid)*lazy[x];
	lazy[ls]+=lazy[x],lazy[rs]+=lazy[x],lazy[x]=0;
}

当然，如果你记录了区间范围，那么这部分会显得容易些：

void pushdown(int x,int l,int r) { //将x节点的懒标记下传
	int mid=l+r>>1;
	sum[ls]+=(mid-l+1)*lazy[x],sum[rs]+=(r-mid)*lazy[x];
	lazy[ls]+=lazy[x],lazy[rs]+=lazy[x],lazy[x]=0;
}

下传时，只下传一层即可，下传多层同样会浪费时间。

区间查询 - query

与区间修改相同，对于给定的区间 \([l,r]\)，我们把它拆成尽量少的多个区间，使得在线段树中存在若干个节点直接代表拆开后的区间，并对这些区间进行查询，最后输出这些区间查询值的和。

在查询时，如果访问了具有懒标记的节点的子节点，也要记得下传。

代码如下：

long long query(int x,int L,int R,int l,int r) {
	int M=L+R>>1;
	if(l<=L && r>=R) return sum[x];
	if(l>R || r<L) return 0;
	pushdown(x,L,R);
	return query(ls,L,M,l,r)+query(rs,M+1,R,l,r);
}

多个懒标

上面的内容已经足以通过 模板题：P3372 【模板】线段树 1 了，我们继续结合 模板题：P3373 【模板】线段树 2 讲解一下进阶的操作

在这道题中，我们需要一种新的操作：区间乘。

有聪明的同学可能要说了：我们也像加法一样，为乘法准备一个 独立的懒标记和下传函数 不就可以了吗？

但是，这两个懒标记之间毫无关系吗？显然不是的。

经过简单的推论，我们可以得出：

  • 进行区间乘时，该节点的加法和乘法懒标记 也要同时 进行乘法。
  • 两个懒标记必须 同时下传。
  • 在下传时，子节点的加法和乘法懒标记 都要进行乘法。
  • 传递的顺序应该是 先乘后加。

所以，在同时存在多个修改操作时，必须注意各个懒标记之间的联系。

还要注意，乘法懒标记的初始值应为 1。

\(\text{AC CODE }\) here

树链剖分

基本概念

我们这里说的树链剖分指的是 重链剖分。首先，我们先来介绍几个简单的概念。

树剖图例

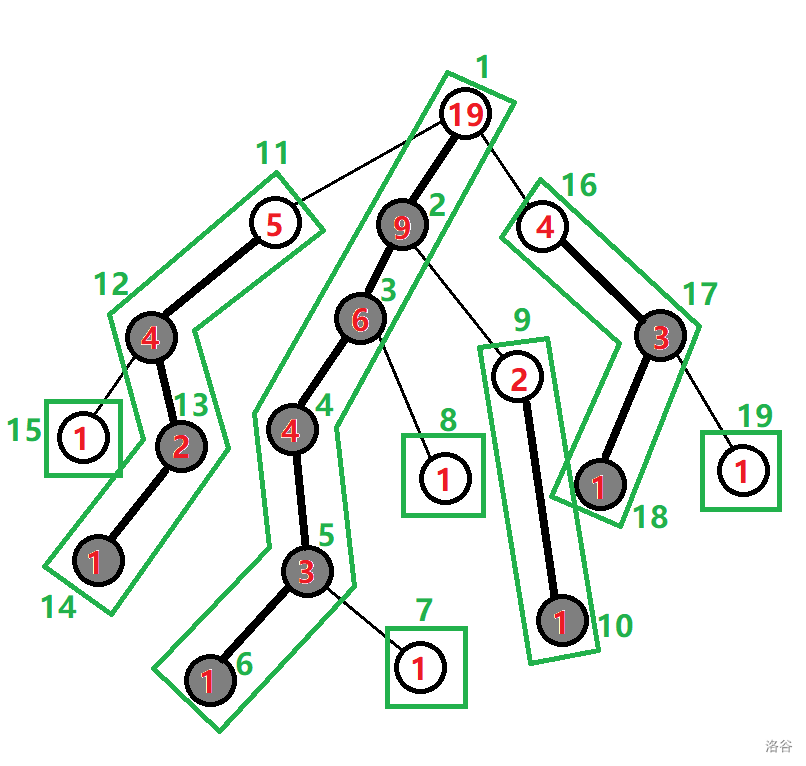
从 OI - WIKI 借了半张图。（之所以是半张图是因为 TSOI 的树剖做法和大众做法略有不同）我们开始介绍：

  • 重儿子：一个节点子节点中子树最大的子节点。图中的灰色节点都是重儿子。
  • 轻儿子：与重儿子对应，除了重儿子之外的所有子节点都是轻儿子。
  • 重边：从当前节点到其重儿子的边。图中的加粗边都是重边。
  • 轻边：从当前节点到其轻儿子的边。
  • 重链：由若干条重链首尾衔接构成的路径。
  • 链深度：这便是 TSOI 与大众做法不同的地方——在树剖中，我们记录的节点深度 \(dep_u\) 表示从 \(u\) 到根节点的路径经过了几条重链。（落单的节点也算做一条重链）

接下来我们要引入一个老朋友，并让他发挥新的作用。

DFS 序

其实就是 tarjan 算法 中的时间戳啦~

DFS 序有一个特点，就是 一棵子树的所有节点 的DFS 序是 相邻的。比如这棵树：
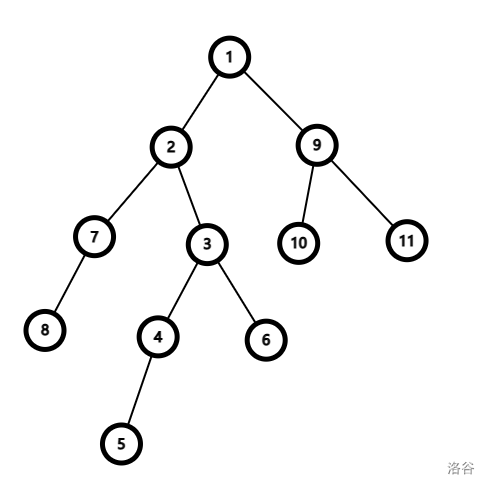
DFS 序图例
用 DFS 序排完后，子树 \(subtree_4\) 的所有节点的 DFS 序正好是 \([4,8]\)。（子树的区间左边界就是这棵子树根节点的 DFS 序，收集子树的区间右边界可以在 DFS 时进行）

如果在 DFS 时优先遍历重儿子，那么 一条重链上的所有节点 的DFS 序也是 相邻的。比如重链 \(1 \to 2 \to 3 \to 4 \to 5\)。

由此一来，我们就可以对一棵树进行 重链剖分 ，然后对 DFS 序建立 线段树，把 路径/子树改变和查询问题 转换成若干个 区间改变和区间查询问题 了。

重剖 LCA

一般来说，树上操作分为两类：

  • 子树操作：直接对子树的 DFS 序区间进行操作即可。
  • 路径操作：需要拆成多个区间。

如何将路径转换为区间？考虑求 LCA，我们用\(fa_u\) 代表 \(u\) 的父节点；用 \(root_u\) 代表 \(u\) 所在重链的最小 DFS 序节点，如上图中:

\[root_5=root_4=root_3=root_2=root_1=1 \]

下文全部用 DFS 序描述节点，码代码时注意标号和 DFS 序的切换。

接下来，对于路径 \(u \to v\)，我们拆成如下几个区间：

  1. 链深度不同：深度更深的节点 \(u\) 跳转至 \(fa_{root_u}\)，\([root_u,u]\) 是需要进行操作的区间；
  2. 链深度相同且 \(root_u \not= root_v\)：\(u\) 跳转至 \(fa_{root_u}\)，\(v\) 跳转至 \(fa_{root_v}\)，\([root_u,u]\) 和 \([root_v,v]\) 是需要进行操作的区间；
  3. 链深度相同且 \(root_u = root_v\)：\([u,v]\) 是需要进行操作的区间之一（\(u<v\)） ，结束。

说起来也不是那么难？三道题送给大家：P4092 [HEOI2016/TJOI2016]树、【模板】重链剖分/树链剖分、P2486 [SDOI2011]染色。这里是后两道题的 \(AC\) \(CODE\)，祝你好运……

讲讲 染色

关于 P2486 [SDOI2011]染色，可以给你一些提示，我好不容易总结出的 “ 王氏染色定则 ” ：

在 染色 这道题中，路径修改具有如下三个特性：

  1. 层次性：对一条有根树重链剖分，链深度 高 的点的 DFS 序一定比链深度 低 的点大
  2. 对称单调性：两点的路径经过的所有节点的 DFS 序组成的 有序序列 从两点的 最近公共祖先 向两边 严格递增。
  3. 方向性：该序列从 最近公共祖先 拆分为 两段 后，每一段即为最近公共祖先到这两点中一点的 路径。

DFS 序图例

举个例子：

  1. \(11\) 的 DFS 序比 \(8\) 大（\(dep_8=2,dep_{11}=3\)）
  2. 这条路径组成的有序序列是：\([8,7][2,1][9,9][11,11]\)（一个区间代表跨过了一条链），这个序列从 \(\operatorname{lca}(8,11)=1\) 向两边严格递增。
  3. 从 \(1\) 处拆开，\([1,2][7,8]\) 和 \([1,1][9,9][11,11]\) 就是 \(1 \to 8\) 和 \(1 \to 11\) 的路径。

希望可以给你写路径查询的代码一些启发。

有问题随时补充，目前就是这样。

树上差分

这里顺便小提一嘴树上差分。顾名思义，和差分逻辑相同，只不过用在了树上。

如果想给路径 \(u \to v\) 的所有节点都加上 \(k\) ，树上差分时，就进行如下操作：

\[diff_u \gets diff_u+1 \]

\[diff_v \gets diff_v+1 \]

\[diff_{\operatorname{lca}(u,v)} \gets diff_{\operatorname{lca}(u,v)}-1 \]

\[diff_{fa(\operatorname{lca}(u,v))} \gets diff_{fa(\operatorname{lca}(u,v))}-1 \]

代码如下：

void make_diff()
{
	for(int i=1;i<n;++i)
	{
		int LCA=lca(a[i],a[i+1]);
		diff[fa[a[i]][0]]++;
		diff[a[i+1]]++;
		diff[LCA]--;
		diff[fa[LCA][0]]--;
	}
}

(结合下面 LCA 的代码哦)

计算最终结果的方法有很多，可以用 dfs 序的逆序，也可以先拓扑排序。

看完 LCA，你就可以试试做一下 P3258 [JLOI2014]松鼠的新家 了，它相当于 LCA 和树上差分的模板题。

动态开点线段树

很好，你已经掌握了初级的线段树。搭配上树链剖分或树上差分，你就可以解决大部分树上问题了。你可以试试解决区间加等差数列，区间加斐波那契数列，文艺线段树 等奇奇怪怪的东西，他们都可以用树剖或树上差分解决。当然，有的时候你需要使用 权值线段树，比如查询第 \(k\) 大之类的。权值线段树就是 用下标代表数的大小，节点值代表出现次数 的线段树。

但是，当我拿出这个数据范围，阁下又如何应对：

\[0 \leq a_i \leq 10^{9} \]

对吧，你总不能开 \(N=1e9\) 的数组吧，更何况线段树是 \(4N.\) 现在晓得 动态开点 的重要性了吧。

抛弃那个没什么用的 x<<1 和 x<<1|1，使用 \(ls_x\) 和 \(rs_x\) 记录 \(x\) 的左儿子和右儿子，\(node\) 记录节点总数。动态开点就别再使用懒标啦，容易出事。你只需要：

void change(int l,int r,int p,int &x,int v) {
	if(!x) x=++node; val[x]+=v；
	if(l==r) return;
	int mid=l+r>>1;
	if(p<=mid) change(l,mid,p,ls[x],v);
	else change(mid+1,r,p,rs[x],v);
}
int query(int x,int L,int R,int l,int r) {
	if(l<=L && r>=R) return sum[x];
	if(l>R || r<L || !x) return 0;
	int M=L+R>>1,ans=0;
	ans+=query(ls[x],L,M,l,r)+query(rs[x],M+1,R,l,r);
	return ans;
}

差不多就是这个意思，自己启发式思考吧。

对了，有时候可以用 pushup，有时候实现成本太高。自己决定。

标记永久化

比如维护区间和：

ll query(int x,int L,int R,int l,int r) {
	if(l<=L && r>=R) return sum[x]+lazy[x]*(r-l+1);
	if(l>R || r<L) return 0;
	ll ans=lazy[x]*(r-l+1);
	int M=L+R>>1;
	return ans+=query(ls,L,M,l,r)+query(rs,M+1,R,l,r);
}

可持久化线段树 / 主席树

如果我想查询历史信息，阁下又如何应对？有没有从动态开点线段树上得到点启发？

我们只需要每修改一个节点就多开一个节点就可以了。

一般来说我们用的都是 可持久化权值线段树，即 主席树。

给个板，【模板】可持久化线段树 2：

#include<bits/stdc++.h>
#define ll long long
const int N=1e6+6;
int tot,a[N],b[N],cnt,n,m,rt[N];
struct node {int ls,rs,sum;} nd[N<<5];
int change(int o,int d,int l,int r) {
	int x=++tot; nd[x]=nd[o],nd[x].sum++;
	if(l==r) return x;
	int mid=(l+r)>>1;
	if(d<=mid) nd[x].ls=change(nd[x].ls,d,l,mid);
	else nd[x].rs=change(nd[x].rs,d,mid+1,r);
	return x;
}
int query(int lo,int ro,int l,int r,int k) {
	if(l==r) return l;
	int los=nd[lo].ls,ros=nd[ro].ls;
	int nsum=nd[ros].sum-nd[los].sum;
	int mid=(l+r)>>1;
	if(k<=nsum) return query(nd[lo].ls,nd[ro].ls,l,mid,k);
	else return query(nd[lo].rs,nd[ro].rs,mid+1,r,k-nsum);
}
int main() {
	std::ios::sync_with_stdio(false);
	std::cin.tie(nullptr);std::cout.tie(nullptr);
	std::cin>>n>>m;
	for(int i=1;i<=n;++i) {std::cin>>a[i]; b[i]=a[i];}
	std::sort(b+1,b+1+n),cnt=std::unique(b+1,b+1+n)-b-1;
	for(int i=1;i<=n;++i) {
		a[i]=std::lower_bound(b+1,b+1+cnt,a[i])-b;
		rt[i]=change(rt[i-1],a[i],1,n);
	}
	for(int i=1;i<=m;++i) {
		int l,r,k; std::cin>>l>>r>>k;
		std::cout<<b[query(rt[l-1],rt[r],1,n,k)]<<'\n';
	}
	return 0;
}

线段树合并 / 线段树分裂

同样建立在动态开点的基础上。理论先咕了吧……

给个模板题代码：

合并：

#include<bits/stdc++.h>
#define ll long long
const int N=1e5+5;
int n,m;
int cnt,head[N];
struct edge { int to,next; } E[N<<1];
void add(int u,int v) { E[++cnt].to=v,E[cnt].next=head[u],head[u]=cnt; }
//dfs & lca module
int tot,dep[N],dfn[N],f[20][N],fa[N],lg[N];
int get(int x,int y) { return dep[x]<dep[y]?x:y; }
void dfs(int u,int father) {
	f[0][dfn[u]=++tot]=father,dep[u]=dep[fa[u]=father]+1;
	for(int p=head[u],v=E[p].to;p;p=E[p].next,v=E[p].to) if(v!=father) dfs(v,u);
}
void init() {
	lg[0]=-1;
	for(int i=1;i<=tot;++i) lg[i]=lg[i>>1]+1;
	for(int j=1;j<=lg[tot];++j)
		for(int i=1;i+(1<<j)-1<=n;++i)
			f[j][i]=get(f[j-1][i],f[j-1][i+(1<<j-1)]);
}
int LCA(int u,int v) {
	if(u==v) return u;
	if((u=dfn[u])>(v=dfn[v])) std::swap(u,v);
	int d=lg[v-u++];
	return get(f[d][u],f[d][v-(1<<d)+1]);
}
//segment_tree module
int node,ls[N<<6],rs[N<<6],val[N<<6],mx[N<<6];
void pushup(int x) {
	val[x]=std::max(val[ls[x]],val[rs[x]]);
	mx[x]=val[x]==val[ls[x]]?mx[ls[x]]:mx[rs[x]];
}
void pushup(int x,int y,int z) { val[z]=val[x]+val[y],mx[z]=mx[x]; }
void change(int l,int r,int p,int &x,int v) {
	if(!x) x=++node;
	if(l==r) return val[x]+=v,mx[x]=p,void();
	int mid=(l+r)>>1;
	if(p<=mid) change(l,mid,p,ls[x],v);
	else change(mid+1,r,p,rs[x],v);
	pushup(x);
}
void merge(int l,int r,int x,int y,int &z) {
	if(!x||!y) return z=x|y,void();
	int mid=(l+r)>>1;
	if(l==r) return pushup(x,y,z);
	merge(l,mid,ls[x],ls[y],ls[z]);
	merge(mid+1,r,rs[x],rs[y],rs[z]);
	return pushup(z);
}
//second dfs module
int rt[N],ans[N];
void NB_dfs(int u) {
	for(int p=head[u],v=E[p].to;p;p=E[p].next,v=E[p].to) if(v!=fa[u]) NB_dfs(v),merge(1,N,rt[u],rt[v],rt[u]);
	ans[u]=val[rt[u]]?mx[rt[u]]:0;
}
//main
int main() {
	std::ios::sync_with_stdio(false);
	std::cin.tie(nullptr); std::cout.tie(nullptr);
	std::cin>>n>>m;
	for(int i=1,a,b;i<n;++i) {
		std::cin>>a>>b;
		add(a,b),add(b,a);
	}
	dfs(1,0),init();
	for(int i=1;i<=m;++i) {
		int x,y,z; std::cin>>x>>y>>z; int lca=LCA(x,y);
		change(1,N,z,rt[x],1);
		change(1,N,z,rt[y],1);
		change(1,N,z,rt[lca],-1);
		if(fa[lca]) change(1,N,z,rt[fa[lca]],-1);
	}
	NB_dfs(1);
	for(int i=1;i<=n;++i) std::cout<<ans[i]<<'\n';
	return 0;
}

分裂：

#include<bits/stdc++.h>
#define ll long long
const int N=2e5+5;
int node,ls[N<<5],rs[N<<5];
ll sum[N<<5];
int n,m,rt[N],a[N],cnt;
void pushup(int x) { sum[x]=sum[ls[x]]+sum[rs[x]]; }
void pushup(int x,int y,int z) { sum[z]=sum[x]+sum[y]; }
void build(int l,int r,int &x) {
	x=++node;
	if(l==r) return sum[x]=a[l],void();
	int mid=l+r>>1;
	build(l,mid,ls[x]),build(mid+1,r,rs[x]);
	pushup(x);
}
void split(int l,int r,int x,int &y,int v) {
	if(!x) return;
	int mid=l+r>>1;
	if(v<mid) std::swap(rs[x],rs[y=++node]),split(l,mid,ls[x],ls[y=++node],v);
	else split(mid+1,r,rs[x],rs[y=++node],v);
	pushup(x),pushup(y);
}
void merge(int x,int y,int &z) {
	if(!x||!y) return z=x|y,void();
	if(!z) z=++node;
	merge(ls[x],ls[y],ls[z]);
	merge(rs[x],rs[y],rs[z]);
	pushup(x,y,z);
}
void change(int l,int r,int p,int &x,int v) {
	if(!x) x=++node;
	if(l==r) return sum[x]+=v,void();
	int mid=l+r>>1;
	if(p<=mid) change(l,mid,p,ls[x],v);
	else change(mid+1,r,p,rs[x],v);
	pushup(x);
}
void split(int x,int l,int r) {
	int tmp;
	split(1,n,rt[x],rt[++cnt],l-1);
	split(1,n,rt[cnt],tmp,r);
	merge(rt[x],tmp,rt[x]);
}
ll query(int L,int R,int x,int l,int r) {
	if(L==l && R==r) return sum[x];
	int mid=L+R>>1;
	if(r<=mid) return query(L,mid,ls[x],l,r);
	else if(l>mid) return query(mid+1,R,rs[x],l,r);
	else return query(L,mid,ls[x],l,mid)+query(mid+1,R,rs[x],mid+1,r);
}
int kth(int l,int r,int x,ll k) {
	if(l==r) return l;
	int mid=l+r>>1;
	if(k>sum[ls[x]]) return kth(mid+1,r,rs[x],k-sum[ls[x]]);
	else return kth(l,mid,ls[x],k);
}	
int main() {
	std::ios::sync_with_stdio(false);
	std::cin.tie(nullptr); std::cout.tie(nullptr);
	std::cin>>n>>m;
	for(int i=1;i<=n;++i) std::cin>>a[i];
	build(1,n,rt[++cnt]);
	for(int i=1,opt;i<=m;++i) {
		ll a,b,c; std::cin>>opt>>a>>b;
		switch(opt) {
			case 0: std::cin>>c; split(a,b,c); break;
			case 1: merge(rt[a],rt[b],rt[a]); break;
			case 2: std::cin>>c; change(1,n,c,rt[a],b); break;
			case 3: std::cin>>c; std::cout<<query(1,n,rt[a],b,c)<<'\n'; break;
			case 4: std::cout<<(sum[rt[a]]<b?-1:kth(1,n,rt[a],b))<<'\n';
		}
	}
	return 0;
}

平衡树

BST 引入，Splay 先咕捏。

非旋 treap

分块

分块和线段树并非毫无相似之处，值得一提的是，分块 是一种 思想，实质上是一种是通过分成多块后在每块上打标记以实现快速区间修改，区间查询的一种算法，而非 数据结构。

具体来说，线段树是向下二分查找修改区间，而分块更加暴力一些。对于一次区间操作，对区间內部的 整块 进行整体的操作（比如 打懒标记），对区间边缘的零散块单独 暴力处理。所以分块被称为“ 优雅的暴力 ”。

其实，上面的两道线段树例题用分块也是能过的，大家可以去试一下。

分块的块数一般为 \(\sqrt{n}\) 个。 所以说分块的时间复杂度大约为 \(O(\sqrt n)\)，是一种 根号算法，可能比线段树这类 对数级 的要慢一些。但是时间差距不大，而且比线段树好写好想，所以焦头烂额的时候就试试分块吧。

这里推荐一道题：P1503 鬼子进村

具体实现嘛……很简单，分块、打懒标，这里就不赘述了，就说说维护需要的变量：

  • \(belong_x\)：表示 \(x\) 这个元素属于哪个分块。
  • \(lazy_x\)：懒标记，同线段树。
  • \(L_x\) 和 \(R_x\)：划定第 \(x\) 个块的区间范围。

仅此而已。

ST 表

引入

ST 表是解决 可重复贡献问题 的数据结构。

什么是可重复贡献问题呢？举个例子，区间最大值，\(\max[1,5]\) 就是 \(\max(\max[1,4],\max[3,5])\) ，虽然 \([3,4]\) 重合了，但并不影响结果，这就是 可重复贡献。相反，区间和就不是可重复贡献问题，同一个部分不能多次被计算。

可重复贡献问题还要满足结合律，也就是说运算 \(\operatorname{opt}\) 的查询是可重复贡献问题，就必须满足：

\[(x\operatorname{opt} y) \operatorname{opt} z = x\operatorname{opt} (y \operatorname{opt} z) \]

RMQ 问题，即区间最大（小）值，和 \(\gcd\) 都是可重复贡献问题。

ST表运用了 倍增 的思想。通过 ST 表，我们可以实现 \(O(n \log n)\) 预处理，\(O(1)\) 查找。

简单来说，倍增思想就是把线性的处理转化为对数级的处理。

这里我们结合 【模板】ST 表，以最大值为例。

预处理

我们用 \(st(i,j)\) 代表区间 \([i,i+2^j-1]\) 的最大值。也就是说 \(st(i,1)\) 就是第 \(i\) 个数本身。我们先来思考递推式。
5,4,3,2,1——想出来了？揭晓答案：

\[st(i,j)=\max (st(i,j-1),st(i+2^{j-1},j-1)) \]

通过这个递推式完成 \(O(n \log n)\) 的预处理，接下来的查找就好办了。

代码如下：

void init()
{
	for(int j=1;j<=21;++j)//21属于是很极限了，这么写属于是省事，其实不需要到21的
		for(int i=1;i+(1<<j)-1<=n;++i)
			st[i][j]=max(st[i][j-1],st[i+(1<<(j-1))][j-1]);
}

查询

如何得到 \([i,j]\) 的最大值呢？我们说过，RMQ 是一个可重复贡献问题，所以查询的过程很简单：

  1. 如果区间有 \(d\) 个元素，找到最接近 \(d\) 且小于 \(d\) 的 2 的整数次幂，其幂指数为 \(k\)。
  2. 查询 \(\max(st(i,k),st(j-2^k,k))\)

代码如下：

int query(int l,int r)
{
	int bit=log2(r-l+1);
	return max(st[l][bit],st[r-(1<<bit)+1][bit]);
}

要么就预处理 \(\log ,\) 要么就使用函数 log2。二进制拆分是 \(O(\log n)\) 不是 \(O(n)\) 的。

LCA 的倍增算法

LCA，即最近公共祖先。

预处理

LCA 的倍增算法也是倍增家族的一员，和 ST表 有异曲同工之妙，在用倍增解决最近公共祖先问题时我们用 \(fa(i,j)\) 表示点 \(i\) 的第 \(2^j\) 个祖先。所以，\(fa(i,0)\) 其实就是点 \(i\) 的父节点。

学习了 ST 表，LCA 的递推式应该同样问题不大。如下：

\[fa(i,j)=fa(fa(i,j-1),j-1) \]

代码则有一些小小的不同，因为是树，所以需要先遍历一波，确定初始状态 \(fa(i,0)\)。

（被 \(dalao\) 骂代码 shit 一样了 QAQ 放改进版）

void dfs(int x)
{
	for(int i=1;i<=20;++i)	f[x][i]=f[f[x][i-1]][i-1];
	for(auto i:e[x])
    		if(i!=f[x][0])
            		{f[i][0]=x;	dep[i]=dep[x]+1;	dfs(i);}
}

查询

你可能注意到了在搜索中我们记录了每个节点的深度，这也是很重要的一环。在查询两个点的 LCA 时，大致分为以下几个步骤：

  1. 深度深的一点向上跳转至他的祖先节点，直至和另一点深度相同。
  2. 深度相同后，两点是同一个节点，则该节点为两点的 LCA。
  3. 深度相同后，两点仍不相同，则继续向上跳转至其祖先节点。
  4. 如果两个节点的祖先节点相同，则不要跳转，这个祖先节点可能不是两点的 最近 公共祖先。当两个点的父节点相同时，该父节点是两点的 LCA。

文字说可能比较乏味？那我来个图：

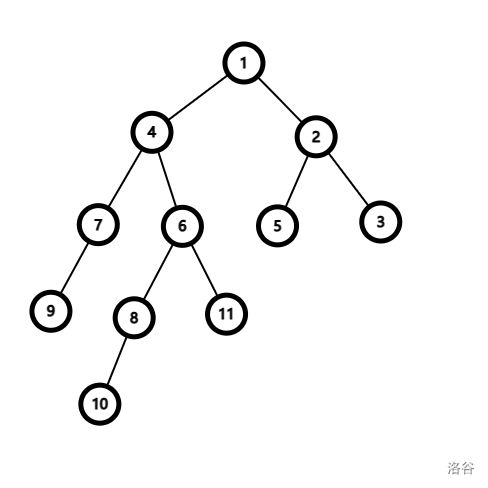
LCA图例

查询 \(10\) 和 \(2\) 的 LCA，操作步骤如下：

  1. \(dep_{10}>dep_2\)，深度差 3。开始跳转：\(10 \to fa(10,1)=6 \to fa(6,0)=4\)。
  2. 同深度，节点不同，继续跳转。两点父节点相同，父节点 \(1\) 就是 \(10\) 和 \(2\) 的 LCA。

大概来说就是这样了，下面是代码：

int LCA(int u,int v)
{
	if(dep[u]<dep[v])	swap(u,v);//个人习惯，每次都让u的深度更深
	int len=dep[u]-dep[v];
	for(int i=20;i>=0;--i)	if(len&(1<<i))	u=f[u][i];//深度差二进制拆分，跳转
	if(u==v)	return u;
	for(int i=20;i>=0;--i)	if(f[u][i]!=f[v][i])	u=f[u][i],v=f[v][i];//只有祖先节点不同才跳
	return f[u][0];
}

字典树 - Trie

顾名思义，一种像字典一样的树，用于应对字符串问题。

字典树示意图

树的每一条边都代表一个字母，从根节点到任何一点的一条简单路径就代表了一个字符串。举个例子，从 \(1\) 到 \(13\) 的简单路径就对应了字符 cab。

简单？我们直接看一下 模板题 的代码。

朴素写法

首先，我们要建立单个字符到数字的映射关系，本题中包含 大小写字母 和 数字，当然，很多情况下只有小写字母，直接 -'a' 也是可以的。

建立映射：

int find(int x) {
	if(x>='0' && x<='9')	return x-'0'+1;
	else if(x>='A' && x<='Z')	return x-'A'+10+1;
	else if(x>='a' && x<='z')	return x-'a'+10+26+1;
}

接下来，我们要解决插入字符串，也很简单，遍历即可：

void insert(std::string s) {
	int now=1,len=s.length();
	for(int i=0;i<len;++i) {
		if(node[now][find(s[i])]) {
			now=node[now][find(s[i])];//node用于指向当前节点的子节点
			cnt[now]++;//cnt用于记录以从根到该点的路径所代表的字符串为前缀的字符串的数量
		}
		else {
			tot++;//tot用于记录总节点数
			now=node[now][find(s[i])]=tot;
			cnt[now]=1；
		}
	}
}

最后，查询，依然是简单粗暴的遍历：

int query(std::string s) {
	int now=1,len=s.length();
	for(int i=0;i<len;++i) {
		if(node[now][find(s[i])])	now=node[now][find(s[i])];
		else return 0;
	}
	return cnt[now];
}

这就是字典树的全部了……吗？

记住这是一道多测题，你需要初始化。什么？memset？相信我，你一定会 T 的。所以，我们有几种很新的方法。

优化：时间戳写法

这里我们引入一个新的变量 \(check_i\) ，记录节点 \(i\) 上一次更新是在哪一组数据。如果当前的数据组数与 \(check_i\) 不同，就初始化节点 \(i\)。选择性初始化时一个不错的降低复杂度的选择。

同时，我们初始化其实只需要重置 \(cnt\) 数组即可，因为我们可以一直沿用当前字典树结构。

\(AC \ CODE\)

#include<bits/stdc++.h>
const int N=3e6+6;
int node[N][65],cnt[N],tot=1,T,n,q,Time=0,check[N];
int find(int x) {
	if(x>='0' && x<='9')	return x-'0'+1;
	else if(x>='A' && x<='Z')	return x-'A'+10+1;
	else if(x>='a' && x<='z')	return x-'a'+10+26+1;
}
void insert(std::string s) {
	int now=1,len=s.length();
	for(int i=0;i<len;++i) {
		if(node[now][find(s[i])]) { 
			now=node[now][find(s[i])];
			if(check[now]==Time)	cnt[now]++;
			else	cnt[now]=1,check[now]=Time;
		}
		else {
			tot++;
			now=node[now][find(s[i])]=tot;
			cnt[now]=1,check[now]=Time;
		}
	}
}
int query(std::string s) {
	int now=1,len=s.length();
	for(int i=0;i<len;++i) {
		if(node[now][find(s[i])])	now=node[now][find(s[i])];
		else return 0;
	}
	return check[now]==Time?cnt[now]:0;
}
int main(){
	std::cin>>T;
	while(T--) {
		Time++;
		std::cin>>n>>q;
		for(int i=1;i<=n;++i) {
			std::string s;
			std::cin>>s;
			insert(s);
		}
		for(int i=1;i<=q;++i) {
			std::string s;
			std::cin>>s;
			std::cout<<query(s)<<'\n';
		}
	}
	return 0;
}

接下来我们见见更多的题。

更多题目

UVA11488 Hyper Prefix Sets

是的，我放的是洛谷的链接。因为考虑到 UVA 定时爆炸，放洛谷应该会方便些吧。这道题其实就是多了一个前缀长度，遍历所有节点算一下 \(cnt \times dep\) 的最大值就可以了。
不过不知道为什么我 T 了，后来改成 memset 奇迹的过了，所以推荐优化可以使用标记清空写法，时间戳有点费脑子。

HDU-1251 统计难题

放的 vjudge。没什么可说的，基本就是模板，但是注意因为判断插入和查询是空行，所以第一次输入可以用 getline，第二次记得让 while 循环停下来。

std::string s;
while(getline(std::cin,s)) {
	if(s=="")	break;
	insert(s);
}
while(getline(std::cin,s)) {
	if(s=="")	break;
	std::cout<<query(s)<<'\n';
}

P5335 [THUSC2016]补退选

这可是一道好题啊，好题啊。

我们考虑不需要上一次查询 ANS 的情况，如何查找前缀为 \(S\) 的学生数量超过要求 \(k\) 的最小事件数呢？

一种是暴力，一个事件查一次，复杂度爆炸；
另一种是我们可以使用一个 vector 记录，如 \(rec(i,k)\) 代表节点 \(i\) 第一次人数为 \(k\) 人时的事件数，最后查询要求的 \(rec(i,k)\) 即可。

接下来考虑在线，使用第二种方法，线性复杂度，绝对没问题。
建议在线查询，离线的话还需要判定你查询的结果是否大于当前事件数……挺难办的。

字典树就到这里了，接下来来说说搜索。

posted @ 2023-05-10 20:00  二两碘酊  阅读(28)  评论(0)  编辑  收藏  举报