ZROI 学习笔记之字符串串
嘿嘿嘿……字符串……我的串串……
都别催!!!等我有时间了例题和详细讲解都会补回来的!!!
CHANGE LOG
- 2023.9.1 将博客 关于数据结构 的字典树部分迁移到此博客,补充 8 月 6 日 KMP、AC 自动机相关内容,补充 8 月 5 日最小表示法与 Manacher 代码。
- 2023.9.2 补充 Z 算法代码。
一些约定
在此博客中,为更方便的表示字符串的相关信息,我们使用如下定义:
-
字符集:一般记作 \(\Sigma\),是一个包含可能的所有输入字符的、建立了全序关系的集合,具体视题目而定。一般是一个泛性的概念。\(\Sigma\) 中的元素称为 字符。
全序关系:\(\Sigma\) 中的任意两个不同的元素 \(\alpha\) 和 \(\beta\) 都可以比较大小,要么 \(\alpha<\beta\),要么 \(\beta<\alpha\)。
-
字符串:由 \(n\) 个字符顺次排列形成的序列,\(n\) 称为 \(S\) 的长度,表示为 \(|S|\)。
-
字符 与 子串:对于一个字符串 \(S\),本文中,我们使用 \(S[i-1]\) 或 \(S_{i-1}\) 表示其第 \(i\) 个字符,即 下标从零开始,这点务必注意。使用 \(S[i\dots j]\) 来代表顺次排列的 \(S[i],\dots,S[j]\) 形成的字符串,即 \(S\) 从 \(i-1\) 到 \(j-1\) 个字符形成的子串。
8.5 - 基础字符串算法
1. 哈希
1.1 哈希函数
考虑实现一个哈希函数 \(h: S \to \mathbf{Z}\),其中 \(S\) 指一个字符串,把输入字符串映射到一个较小、方便比较的值域中。这个哈希函数一般是 \(h(S) = ( \sum_{i=0}^{ |S|-1} S_i \cdot a^i ) \bmod p\),其中 \(a\) 是一个自定的、应 \(\geq |S|\) 的任意整数。
1.2 哈希冲突
一个经典的例子是 生日冲击问题。
生日问题 / 生日悖论:如果想让一群人中至少有两个人生日相同,根据鸽巢原理,我们需要 367 个人;但如果是想让至少两个人生日相同的概率达到 \(99.9%\),只需要 \(70\) 个人;而如果概率是 \(50%\),那么只需要 \(23\) 个人就够了。
生日冲击问题告诉我们,函数对随机数据映射产生冲突的概率是指数级增长的。对于一个值域是 \([1,m]\) 的函数,\(\sqrt{m}\) 个数就可以让映射冲突的概率大于 \(\dfrac{1}{2}\),对于哈希函数也同理。
1.3 双哈希 / 多哈希
于是,我们可以考虑构造多个哈希函数,比如选取不同的模数 \(p\)。这样,我们可以大概认为,两个字符是相同的,当且仅当他们的所有哈希函数都对应相同。
在具体做题中,通过预处理所有前缀 / 后缀的 hash 值得到 \(O(1)\) 计算所有子串的方法,从而 \(O(1)\) 判断子串是否相等,是一种常见的应用。
2. 字典树 - Trie
这个词念 [triː],或者 [traɪ]。
顾名思义,一种像字典一样的树,用于应对字符串问题。

树的每一条边都代表一个字母,从根节点到任何一点的一条简单路径就代表了一个字符串。举个例子,从 \(1\) 到 \(13\) 的简单路径就对应了字符 cab。
简单?我们尝试 模板题 的代码。
2.1 朴素写法
首先,我们要建立单个字符到数字的映射关系,本题中包含 大小写字母 和 数字,当然,很多情况下只有小写字母,直接 -'a' 也是可以的。
建立映射:
inline int trans(int x) {
if(x>='0' && x<='9') return x-'0'+1;
else if(x>='A' && x<='Z') return x-'A'+10+1;
else if(x>='a' && x<='z') return x-'a'+10+26+1;
}
接下来,我们要解决插入字符串,也很简单,遍历即可:
inline void insert(std::string s) {
int now=0,len=s.length();
for(int i=0;i<len;++i) {
int to=trans(s[i]);
!node[now][to]&&(node[now][to]=++tot);
now=node[now][to],++cnt[now]; // node用于指向当前节点的子节点,cnt用于记录以从根到该点的路径所代表的字符串为前缀的字符串的数量
}
}
最后,查询,依然是简单粗暴的遍历:
inline int query(std::string s) {
int now=0,len=s.length();
for(int i=0;i<len;++i) {
if(node[now][trans(s[i])]) now=node[now][trans(s[i])];
else return 0;
}
return cnt[now];
}
这就是最简单、也是最常用的 Trie 写法了。
一棵本身也是二叉树,两个儿子分别表示 0 和 1 的字典树被称为 01trie。Trie 按位存储字符串(\(k\) 进制串)的信息,有着很好的性质。比如找
字典树的插入与查询可以简单地通过循环实现,也可以像线段树一样,通过递归实现。一般来讲,循环在空间占用、码量上来说更加优秀;但如果是 可持久化 Trie 或 双指针查询 等实现更加复杂的情况,递归则会在编写难度和稳定性上展现出一定优势。两种写法各有利弊,可以视具体情况而定。
在多测时,直接清空所有字典树数据在时间上并不优秀,所以我们介绍一种针对多测的优化。
2.2 优化:时间戳写法
这里我们引入一个新的变量 \(check_i\),即 时间戳,记录节点 \(i\) 上一次更新是在哪一组数据。如果当前的数据组数与 \(check_i\) 不同,就初始化节点 \(i\)。选择性初始化是一个不错的降低复杂度的选择。
同时,我们初始化其实只需要 重置 \(cnt\) 数组 即可,因为我们可以一直 沿用当前字典树结构。
\(\text{AC Code}\)
#include<bits/stdc++.h>
const int N=3e6+6;
int node[N][65],cnt[N],tot,T,n,q,Time=0,check[N];
inline int trans(int x) {
if(x>='0' && x<='9') return x-'0'+1;
else if(x>='A' && x<='Z') return x-'A'+10+1;
else if(x>='a' && x<='z') return x-'a'+10+26+1;
}
inline void insert(std::string s) {
int now=0,len=s.length();
for(int i=0;i<len;++i) {
int to=trans(s[i]);
!node[now][to]&&(node[now][to]=++tot);
now=node[now][to];
check[now]^Time&&(cnt[now]=0,check[now]=Time);
++cnt[now];
}
}
int query(std::string s) {
int now=0,len=s.length();
for(int i=0;i<len;++i) {
if(node[now][trans(s[i])]) now=node[now][trans(s[i])];
else return 0;
}
return check[now]==Time?cnt[now]:0;
}
int main(){
std::cin>>T;
while(T--) {
Time++;
std::cin>>n>>q;
for(int i=1;i<=n;++i) {
std::string s;
std::cin>>s;
insert(s);
}
for(int i=1;i<=q;++i) {
std::string s;
std::cin>>s;
std::cout<<query(s)<<'\n';
}
}
return 0;
}
3. 最小表示法
给出一个字符串,求与它循环同构的串中字典序最小的串。
\(O(n)\) 的做法是,比较两个由 \(i,j\) 开头的子串,如果第一个不同的地方是 \(S[i+k],S[j+k]\),且 \(S[i+k]>S[j+k]\),那么 \(S[i\dots i+k]\) 不可能称为最小表示的开头。这时将指针 \(i\) 挪到 \(i+k+1\) 即可,全程就是两个指针 \(i\) 和 \(j\) 在比,指到一起了就找一个往后指一个,直到有一个超出 \(n\)。
// Author: MichaelWong
// Code: C++14(GCC 9)
// Date: 2023/9/1
// File: 【模板】最小表示法.cpp
#include<bits/stdc++.h>
#define ll long long
#define ld long double
#define pii std::pair<int,int>
#define fsp(x) std::fixed<<std::setprecision(x)
#define forE(u) for(int p=head[u],v=to[p];p;p=next[p],v=to[p])
const int N=3e5+5;
int n,a[N<<1],pos,i,j,k;
int main() {
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr); std::cout.tie(nullptr);
std::cin>>n;
for(int i=1;i<=n;++i) std::cin>>a[i],a[i+n]=a[i];
for(i=1,j=2,k;i<=n&&j<=n;) {
for(k=0;k<n&&a[i+k]==a[j+k];++k);
a[i+k]>a[j+k]?i=i+k+1:j=j+k+1;
j+=i==j;
}
pos=std::min(i,j);
for(int i=0;i<n;++i) std::cout<<a[pos+i]<<' ';
return 0;
}
// The code was submitted on Luogu.
// Version: 2.0
// If I filled in nothing on the statement,
// it means I'm in a contest and I have no time to do this job.
4. Manacher
马拉车嘿嘿……
用于统计所有回文子串数量,考虑通过枚举回文中心,寻找当前回文中心的最大回文子串来统计。
维护一个已找到的 \(r\) 最大的回文子串\([l,r]\),如果当前枚举的回文中心 \(i>r\),则暴力向两边尝试扩展,找到最大的回文子串;否则,\(i\) 关于维护的回文子串 \([l,r]\) 的回文中心对称的点 \(j\)(即 \(l+(r-i)\)),\(i\) 的最长回文子串长度至少和 \(j\) 的回文子串在 \([l,r]\) 以内的部分长度相等,从这部分开始尝试向外暴力扩展即可。
// Author: MichaelWong
// Code: C++14(GCC 9)
// Date: 2023/9/1
// File: 【模板】manacher 算法.cpp
#include<bits/stdc++.h>
#define ll long long
#define ld long double
#define pii std::pair<int,int>
#define fsp(x) std::fixed<<std::setprecision(x)
#define forE(u) for(int p=head[u],v=to[p];p;p=next[p],v=to[p])
const int N=1.1e7+7;
int n,ptr,R[N<<1],ans;
char s[N],t[N<<1];
int main() {
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr); std::cout.tie(nullptr);
std::cin>>s+1; n=strlen(s+1),t[++ptr]='(',t[++ptr]='#';
for(int i=1;i<=n;++i) t[++ptr]=s[i],t[++ptr]='#';
t[++ptr]=')';
for(int i=1,c=0,r=0;i<ptr;++i) {
R[i]=r<i?1:std::min(R[c*2-i],r-i+1);
while(t[i-R[i]]==t[i+R[i]]) ++R[i];
ans=std::max(ans,R[i]-1);
if(i+R[i]-1>r) c=i,r=i+R[i]-1;
}
std::cout<<ans<<'\n';
return 0;
}
// The code was submitted on Luogu.
// Version: 1.
// If I filled in nothing on the statement,
// it means I'm in a contest and I have no time to do this job.
Manacher 巧妙的运用了回文串的性质,时间复杂度 \(O(n)\)。Manacher 本身也证明了一个字符串的本质不同回文子串个数不大于 \(n\)。
5. KMP
Knuth-Morris-Pratt 算法,AKA KMP。用于解决单模字符串匹配问题。
在 KMP 中,下标从 0 开始的记法并不方便处理,所以我们在这一部分,我们下标从 1 开始。
5.1 前缀函数
你可能会听到很多不同的表达:
- 最长 \(\operatorname{border}\) / 真 \(\operatorname{border}\);
- next 数组;
- 前缀函数。
其实它们是同一个东西,在这里,我们统一称为 前缀函数。当然,我们也顺便介绍一下什么是 \(\operatorname{border}\)。
一个字符串 \(s\) 的 \(\operatorname{border}\) 是它的一个子串,该子串 既是 \(s\) 的前缀又是 \(s\) 的后缀。
那么什么是前缀函数呢?
一个字符串的 前缀函数 定义为一个长度 \(n\) 的数组 \(\pi , \pi[i]\) 定义为 最长的 \(\operatorname{border}\) 的长度。即:
上文我们说到,KMP 算法中我们一般从
1开始,所以这章中我们所说的前缀函数实际是\[\pi[1] = 0, \pi[i] = \max \limits_{k=0 \dots i} \{ k: s[1 \dots k] = s[i - (k-1) \dots i] \}. \]
5.2 KMP 算法
常见的 KMP 算法有两种实现方法,当我们在待匹配串 \(t\) 中匹配模式串 \(s\) 时:
- 创建一个新的字符串 \(s + \# + t\),\(\#\) 是一个不在 \(s\) 与 \(t\) 中出现的分隔符。计算该字符串的前缀函数,对于每个 \(i>|s|+1\),如果有 \(\pi [i] = |s|\),则证明 \(s\) 在 \(t\) 中的 \(i - (|s|-1) - (|s| + 1) = i - 2 |s|\) 处出现。
- 先对 \(s\) 求前缀函数,然后使用双指针,将 \(s\) 在 \(t\) 中匹配。如果 \(s\) 的下一位与 \(t\) 的下一位相同,则两个指针同时向前走一位,当 \(s\) 的指针指到最后一位时,证明匹配成功;如果不同,\(s\) 的指针下标退回到其前缀函数处,直至下一位相同或无法退回(指针指在最开始)。
8.6 - 进阶算法
1. Z 算法 / 扩展 KMP
确实,和 KMP 没有任何关系。不如叫扩展马拉车。
求解 Z 函数的算法。一个字符串的 Z 函数 \(z_i\) 表示 \(s\) 的第 \(i\) 个后缀与 \(s\) 的最长公共前缀长度。
类似于 Manacher,先鸽了……没有心思写,代码放在这里。
// Author: MichaelWong
// Code: C++14(GCC 9)
// Date: 2023/9/2
// File: 【模板】扩展 KMP(Z 函数).cpp
#include<bits/stdc++.h>
#define ll long long
#define ld long double
#define pii std::pair<int,int>
#define fsp(x) std::fixed<<std::setprecision(x)
#define forE(u) for(int p=head[u],v=to[p];p;p=next[p],v=to[p])
const int N=2e7+7;
std::string s,t;
int slen,tlen,z[N],p[N];
int main() {
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr); std::cout.tie(nullptr);
std::cin>>t>>s; tlen=t.length(),slen=s.length(),t=" "+t,s=" "+s;
z[1]=slen;
for(int i=2,l=0,r=0;i<=slen;++i) {
z[i]=i>r?0:std::min(z[i-l+1],r-i+1);
while(s[1+z[i]]==s[i+z[i]]) ++z[i];
if(i+z[i]-1>r) l=i,r=i+z[i]-1;
}
for(int i=1,l=0,r=0;i<=tlen;++i) {
p[i]=i>r?0:std::min(z[i-l+1],r-i+1);
while(p[i]<slen&&s[1+p[i]]==t[i+p[i]]) ++p[i];
if(i+p[i]-1>r) l=i,r=i+p[i]-1;
}
ll ans=0;
for(int i=1;i<=slen;++i) ans^=1ll*i*(z[i]+1);
std::cout<<ans<<'\n';
ans=0;
for(int i=1;i<=tlen;++i) ans^=1ll*i*(p[i]+1);
std::cout<<ans<<'\n';
return 0;
}
// The code was submitted on Luogu.
// Version: 1.
// If I filled in nothing on the statement,
// it means I'm in a contest and I have no time to do this job.
2. AC 自动机
AC 自动机,即 Aho-Corasick Automaton,AKA ACAM。
自动机,注意是 automaton 而非 automation,是一个数学模型,一般由 AutoMaton 被缩写成 AM。接下来会陆续讲解自动机一类的三个经典案例——ACAM,PAM 和 SAM,而 ACAM 是三个中唯一一个用发明人名字命名的,他的逻辑也和另外两个自动机略有不同。下面,我们先简单介绍一下他们的前置知识——确定有限状态自动机。
2.1 确定有限状态自动机
确定有限状态自动机,即 Deterministic Finite Automaton,AKA DFA。
OI 中提到的 “自动机” 一般都指 DFA。自动机是 OI、计算机科学中被广泛使用的一个数学模型。在字符串算法中,自动机的思想尤为常见。所以,在介绍自动机相关算法之前,我们需要简单了解什么是自动机。
在 OI Wiki 上有关于 DFA 详细的讲解,在这里,我聊聊我片面的看法。在 OI 中,自动机的呈现方法是一张 有向图。要识别的字符串从 规定的起点(起点状态) 开始,在图上通过 边(转移函数) 在 点(状态) 之间转移。最后在一个 接受状态 结束。这种解释应该会帮助你更形象地理解自动机。
2.2 字典树的构建
ACAM 接受且仅接受以指定的字符串集合中的某个元素为后缀的字符串,即 Trie + KMP。KMP 是 ACAM 的字符串集合大小退化至 \(1\) 的情况,而 Trie 提供了同时处理多个模式串的框架。
ACAM 的第一步就是对给定的模式串集合建立字典树,和普通的字典树相同。
inline void insert(std::string s) {
int now=0;
for(int i=0;i<s.length();++i) {
if(node[now][trans(s[i])]) now=node[now][trans(s[i])];
else now=node[now][trans(s[i])]=++tot;
}
}
2.3 失配指针
失配指针 \(fail_i\) 在 构建自动机 和 统计答案 时发挥了关键作用。失配指针可以看作是 KMP 中 前缀函数 / \(next\) 数组 的 合理外推。我们考虑字符串在一个模式串的位置 \(i\) 失配 的情况:
- KMP:找到 前缀函数,即 \(next_i\) 指到的模式串位置。他的含义是,在模式串中当前位置以前找到一个前缀,使得该 前缀 与当前位置的 后缀 相同,且相同这一段 长度最长。
- ACAM:找到 失配指针,即 \(fail_i\) 指到的字典树节点。他的含义是,在集合中找到一个模式串的前缀,使得该 前缀 与当前模式串 后缀 相同,且相同这一段 长度最长。
相信这样对比,你就明白失配指针在做怎样一件事了。他将 KMP 应对失配的解决方案扩展到了多个模式串的情况。
2.4 失配指针与自动机的构建
我们考虑一下失配指针如何构建。回顾 KMP 构建前缀函数的过程,我们是从上一个位置得到这一个位置的前缀函数。具体来说,使用一个指针 \(ptr\),其初值为 \(ptr = next_{i-1}\),
- 如果 \(s[ptr+1]=s[i]\),则 \(next_i=ptr+1\);
- 否则,令 \(ptr=next_{ptr}\),直至上面条件成立。
在构建失配指针时,我们延续这种方法。具体地,我们令 \(ptr = fail_{fa_i}\),从 \(fa_i\) 到 \(i\) 的这条边字符是 \(to\),
- 如果存在 \(node(ptr,to)\),则 \(fail_i = node(ptr,to)\);
- 否则,令 \(ptr = fail_{ptr}\),直至上面条件成立。
可以发现,依靠父亲构建 \(fail\) 的过程比较繁琐。在 ACAM 中,我们一般对一个节点的所有儿子构建 \(fail\),这样更加简单。令 \(ptr=i\),
- 如果存在 \(node(ptr,to)\),则 \(fail_{node(i,to)} = node(ptr,to)\);
- 否则,令 \(ptr = fail_{ptr}\),直至上面的条件成立。
这样就完成了失配指针的构建。接下来,我们来构建自动机的 转移函数 \(\delta\)。
- \(\delta (i,to)\) 指在节点 \(i\),字符串的下一位字符是 \(to\) 时应该转移到的位置。
形式化的来说,
其中,
- \(\delta (i,to)\) 表示自动机的 转移函数,即自动机呈现的有向图的边;
- \(node(i,to)\) 表示字典树原有的边;
- \(start\) 表示自动机的 起始状态,即字典树的 根,也是 \(node\) 的初值,\(node\) 指向根表示 字典树上没有这个转移。
不难发现一个特点:\(fail\) 和 \(\delta\) 的构建都建立在多次跳 \(fail\) 的基础上,且他们跳 \(fail\) 的条件相同:\(node(i,to) \neq start\)。所以我们可以广义化 \(node\),将它从字典树的边扩展到自动机的边。
失配指针和自动机的构建是同时进行的,这两个构建过程相辅相成,依靠同一个 bfs 实现。
- \(node(i,to) = start\) 时,需要广义 \(node\),即 \(node(i,to) = node(fail_i,to)\),而广义后的 \(node\) 必然指向遍历过的节点,因为 \(fail\) 是向深度浅的方向跳,所以 \(fail_i\) 必然已经被遍历过。\(node(fail_i,to)\) 如果不是原来字典树上的边,也必然已经广义化,故跳一次即可;且 \(fail_{node(i,to)}\) 在遍历 \(fail_i\) 时已经更新,无需再次更新。
- \(node(i,to) \neq start\) 时,不需要广义 \(node\),这条边本来就出现在字典树上。但这是 \(node(i,to)\) 第一次被遍历,\(fail_{node(i,to)}\) 未更新过,需要更新,即 \(fail_{node(i,to)}=node(fail_i,to)\),同样,\(node(fail_i,to)\) 必然被广义化了,跳一次即可。
上面两条可以简化为:
- 认领儿子从失配指针处认领;
- 儿子的失配指针是失配指针的儿子。
可以发现,广义 \(node\) 和更新 \(fail\) 的条件恰好相反,而构建过程又互相需要彼此,所以放在一起再合适不过了。父亲是字典树根的节点除本身之外没有前后缀,所以他们的失配指针显然 指向根。我们可以从这里开始。
inline void build() {
static std::queue<int> q;
for(int i=0;i<26;++i) if(node[0][i]) q.push(node[0][i]);
while(!q.empty()) {
int u=q.front(); q.pop();
for(int i=0;i<26;++i)
if(node[u][i]) fail[node[u][i]]=node[fail[u]][i],q.push(node[u][i]);
else node[u][i]=node[fail[u]][i];
}
}
广义化 \(node\) 数组后,他就成为了自动机的转移函数,字符串就可以直接在 经过加边的字典树 这张 有向图 上不断转移了。这个有向图就是 AC 自动机。
2.5 答案的统计
接下来我们讨论如何进行答案的统计,这部分会和字典树有些异曲同工之妙。
在 【模板】AC 自动机(简单版) 中,我们需要统计有几个字符串出现过。我们需要一个数组 \(cnt\),表示每个节点代表的字符串在 模式串集合 中的 出现次数。我们就可以在插入模式串的过程中更新 \(cnt\)。很简单,只需要在结尾加一句:
++cnt[now];
查询的时候,向字典树一样在自动机上转移:
inline int query(std::string s) {
int ans=0,now=0,len=s.length();
for(int i=0;i<len;++i) {
now=node[now][trans(s[i])];
for(int u=now;u&&cnt[u]!=-1;u=fail[u]) ans+=cnt[u],cnt[u]=-1; // 关键
}
return ans;
}
转移时里面的那个循环是关键。字符串转移到当前节点不仅代表当前节点代表的字符串出现了,也代表 它的失配指针指向的节点代表的字符串同样出现了。所以,我们在统计的过程中要在每个节点进行一次跳失配指针,一直跳到起始状态,将他们的答案都统计进去。因为每个模式串只统计一次,所以遍历一次后将它的 \(cnt\) 改为 \(-1\) 即可,下次跳到这里就可以了。
\(\text{AC Code}\):
#include<bits/stdc++.h>
#define ll long long
#define ld long double
#define pii std::pair<int,int>
#define fsp(x) std::fixed<<std::setprecision(x)
#define forE(u) for(int p=head[u],v=to[p];p;p=next[p],v=to[p])
const int N=1e6+6;
int tot,node[N][26],cnt[N*26],fail[N*26];
inline int trans(char ch) { return ch-'a'; }
inline void insert(std::string s) {
int now=0;
for(int i=0;i<s.length();++i) {
if(node[now][trans(s[i])]) now=node[now][trans(s[i])];
else now=node[now][trans(s[i])]=++tot;
}
++cnt[now];
}
inline void build() {
static std::queue<int> q;
for(int i=0;i<26;++i) if(node[0][i]) q.push(node[0][i]);
while(!q.empty()) {
int u=q.front(); q.pop();
for(int i=0;i<26;++i)
if(node[u][i]) fail[node[u][i]]=node[fail[u]][i],q.push(node[u][i]);
else node[u][i]=node[fail[u]][i];
}
}
inline int query(std::string s) {
int ans=0,now=0,len=s.length();
for(int i=0;i<len;++i) {
now=node[now][trans(s[i])];
for(int u=now;u&&cnt[u]!=-1;u=fail[u]) ans+=cnt[u],cnt[u]=-1;
}
return ans;
}
int n;
std::string s;
int main() {
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr); std::cout.tie(nullptr);
std::cin>>n;
for(int i=1;i<=n;++i) std::cin>>s,insert(s);
build();
std::cin>>s;
std::cout<<query(s)<<'\n';
return 0;
}
而在 加强版 中,我们被要求记录每个字符串的出现次数,所以我们可以给每个字符串在字典树上的终点发一个哈希值,在查询的时候给这个哈希值加 \(1\)。
#include<bits/stdc++.h>
#define ll long long
#define ld long double
#define pii std::pair<int,int>
#define fsp(x) std::fixed<<std::setprecision(x)
#define forE(u) for(int p=head[u],v=to[p];p;p=next[p],v=to[p])
const int N=20005;
int tot,node[N][26],fail[N*26],map[N*26],cnt[N];
inline int trans(char ch) { return ch-'a'; }
inline void init() {
memset(node,0,sizeof node);
memset(fail,0,sizeof fail);
memset(cnt,0,sizeof cnt);
memset(map,0,sizeof map);
tot=0;
}
inline void insert(std::string s,int id) {
int now=0;
for(int i=0;i<s.length();++i) {
if(node[now][trans(s[i])]) now=node[now][trans(s[i])];
else now=node[now][trans(s[i])]=++tot;
}
map[now]=id;
}
inline void build() {
std::queue<int> q;
for(int i=0;i<26;++i) if(node[0][i]) q.push(node[0][i]);
while(!q.empty()) {
int u=q.front(); q.pop();
for(int i=0;i<26;++i)
if(node[u][i]) fail[node[u][i]]=node[fail[u]][i],q.push(node[u][i]);
else node[u][i]=node[fail[u]][i];
}
}
inline void query(std::string s) {
int ans=0,now=0,len=s.length();
for(int i=0;i<len;++i) {
now=node[now][trans(s[i])];
for(int u=now;u;u=fail[u]) ++cnt[map[u]];
}
}
int n;
std::string s[200],t;
int main() {
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr); std::cout.tie(nullptr);
while(std::cin>>n&&n) {
init();
for(int i=1;i<=n;++i) std::cin>>s[i],insert(s[i],i);
build();
std::cin>>t,query(t);
int max=0;
for(int i=1;i<=n;++i) if(cnt[i]>max) max=cnt[i];
std::cout<<max<<'\n';
for(int i=1;i<=n;++i) if(cnt[i]==max) std::cout<<s[i]<<'\n';
}
return 0;
}
2.6 图论类优化
而在 二次加强版 中,普通的 AC 自动机就无法通过了。因为 AC 自动机是一个 有向图,且是一个 DAG,所以我们可以用一些图论类优化来加速它。
我们注意到,在每个节点都跳一次失配指针太费时间了,每次都要跳到底。其实,我们大可以在所有查询都结束之后整体跳一次,也就是 拓扑排序。
#include<bits/stdc++.h>
#define ll long long
#define ld long double
#define pii std::pair<int,int>
#define fsp(x) std::fixed<<std::setprecision(x)
#define forE(u) for(int p=head[u],v=to[p];p;p=next[p],v=to[p])
const int N=2e6+6;
std::map<std::string,int> mp;
int tot,node[N][26],fail[N*26],cnt[N*26],in[N*26];
inline int trans(char ch) { return ch-'a'; }
inline int insert(std::string s,int id) {
int now=0;
for(int i=0;i<s.length();++i) {
if(node[now][trans(s[i])]) now=node[now][trans(s[i])];
else now=node[now][trans(s[i])]=++tot;
}
return now;
}
inline void build() {
std::queue<int> q;
for(int i=0;i<26;++i) if(node[0][i]) q.push(node[0][i]);
while(!q.empty()) {
int u=q.front(); q.pop();
for(int i=0;i<26;++i)
if(node[u][i]) ++in[fail[node[u][i]]=node[fail[u]][i]],q.push(node[u][i]);
else node[u][i]=node[fail[u]][i];
}
}
inline void query(std::string s) {
int ans=0,now=0,len=s.length();
for(int i=0;i<len;++i) now=node[now][trans(s[i])],++cnt[now];
}
inline void topo() {
std::queue<int> q;
for(int i=1;i<=tot;++i) if(!in[i]) q.push(i);
while(!q.empty()) {
int u=q.front(); q.pop();
cnt[fail[u]]+=cnt[u];
if(--in[fail[u]]==0) q.push(fail[u]);
}
}
int n,ord;
std::string s[200005],t;
int main() {
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr); std::cout.tie(nullptr);
std::cin>>n;
for(int i=1;i<=n;++i) {
std::cin>>s[i];
if(mp[s[i]]) continue;
mp[s[i]]=insert(s[i],ord);
}
build();
std::cin>>t;
query(t),topo();
for(int i=1;i<=n;++i) std::cout<<cnt[mp[s[i]]]<<'\n';
return 0;
}
其实这种优化方法大部分时候都用不到。但他给我们的启发是,要准确把握自动机与有向图的关系,许多图论上的方法都会被用在自动机上。
3. 回文自动机
回文自动机,即 Palindromic Automaton,AKA PAM。
3.1 回文树的树形态
PAM 同样由转移边和后缀链接(即 \(fail\) 指针)组成,又被称作回文树(EER Tree,Palindromic Tree)。这是因为他的所有转移边会构成两棵树——分别存储长度为奇数和偶数的回文串。在存储时,我们只存储回文串的一半。
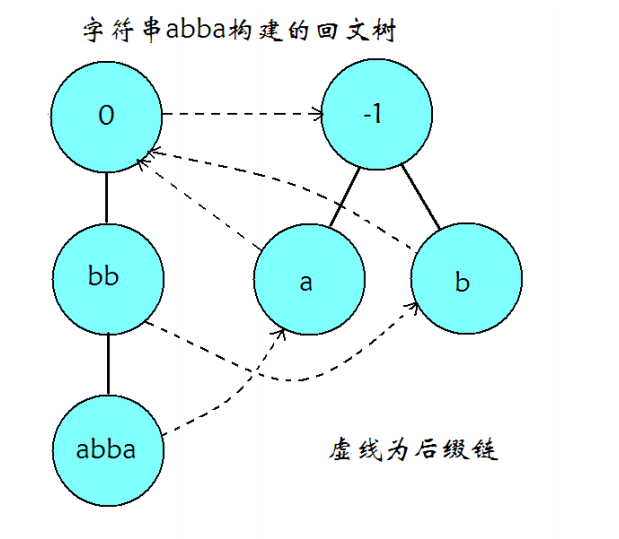
图来自 OI Wiki。
PAM 的转移边代表的是在原回文串的基础上 前后各增加一个字符,因为他需要是 回文 的;而 PAM 的后缀链接 / \(fail\) 指针则指向当前回文串的 最长回文后缀 所代表的节点;我们还需要记录每个节点对应的回文串长度 \(len\),这将对 PAM 的构建提供很大的便利。
3.2 回文树的构建
PAM 和 SAM 的构建都是采用 增量法,这意味着两者的构建都是 在线 的。
回文树的起始状态的两个树的树根,\(len\) 分别为 \(0\) 和 \(-1\)(奇回文串长度为奇数,先用 \(-1\) 退回一个长度),分别称为 偶根 和 奇根。偶根的 \(fail\) 指针指向奇根,而奇根显然 不可能失配,因为他转移到的状态 \(len=1\),单个字符显然是回文串。
接下来,我们考虑采用增量法,在前 \(p-1\) 个字符的 PAM 上构建前 \(p\) 个字符的回文串。
构建的过程很简单,只需要不断跳 \(fail\) 指针,直到找到一个节点使得 \(s_p = s_{p-len-1}\) 即可;\(fail\) 指针则从找到的节点的 \(fail\) 指针开始跳 \(fail\),采用相同的方法。这个过程可以简化成一个函数 \(\operatorname{getfail}(pos,ptr)\),即找到 \(pos\) 节点下一位为 \(s_{ptr}\) 的转移。(这时候你就会发现构建 \(fail\) 指针的方法真的和 ACAM 一样,儿子的 \(fail\) 是 \(fail\) 的儿子。)
inline int getfail(int pos,int ptr) {
while(ptr-len[pos]-1<0||s[ptr-len[pos]-1]!=s[ptr]) pos=fail[pos];
return pos;
}
至此,PAM 的构建就结束了。下面是 P5496 【模板】回文自动机(PAM) 的代码:
// Author: MichaelWong
// Code: C++14(GCC 9)
// Date: 2023/8/7
// File: 【模板】回文自动机(PAM).cpp
#include<bits/stdc++.h>
#define ll long long
#define ld long double
#define pii std::pair<int,int>
#define fsp(x) std::fixed<<std::setprecision(x)
#define forE(u) for(int p=head[u],v=to[p];p;p=next[p],v=to[p])
const int N=5e5+5;
int n,lastans,tot=1,node[N*30][30],len[N*30],fail[N*30],num[N*30];
std::string s;
inline int getfail(int pos,int ptr) {
while(ptr-len[pos]-1<0||s[ptr-len[pos]-1]!=s[ptr]) pos=fail[pos];
return pos;
}
inline void build(std::string &s) {
int now=0,cur=0,dec; fail[0]=1,len[1]=-1,n=s.length();
for(int i=0;i<n;++i) {
s[i]=(s[i]-97+lastans)%26+97;
int to=s[i]-'a'; now=getfail(cur,i);
if(!node[now][to]) {
fail[++tot]=node[getfail(fail[now],i)][to];
len[node[now][to]=tot]=len[now]+2,num[tot]=num[fail[tot]]+1;
}
cur=node[now][to],lastans=num[cur];
std::cout<<lastans<<' ';
}
}
int main() {
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr); std::cout.tie(nullptr);
std::cin>>s;
build(s);
return 0;
}
// The code was submitted on Luogu.
// Version: 1.
// If I filled in nothing on the statement,
// it means I'm in a contest and I have no time to do this job.
8.7 - 后缀数据结构
构造思维复杂,构造代码浮夸,具体用途位置,请让笔者咕下。
1. 后缀数组
Suffix Array,AKA SA。
不是模拟退火!(Simulated Annealing)
2. 后缀自动机
Suffix Automaton,AKA SAM。
8.8 - 杂题选讲
不好说,有空再写
8.9 - 模拟赛
很有说头,但有空再说


 浙公网安备 33010602011771号
浙公网安备 33010602011771号