ZROI 学习笔记之数据结构

都别催！！！等我有时间了例题和详细讲解都会补回来的！！！

CHANGE LOG

2023.8.21 规范文章结构，补充 7 月 17 日相关内容，增加 dfs 序求 LCA，将博客 关于数据结构 部分内容合并到此博客。
2023.8.23 增加 7 月 17 日扫描线部分与习题。
2023.8.24 补充 7 月 17 日 Kruskal 重构树。
2023.8.25 补充 7 月 22 日线段树分治、吉老师线段树。
2023.9.1 将博客 关于数据结构 的动态开点线段树与线段树合并部分迁移到此博客。

7.17 - 基础数据结构

1. 并查集

英文的常见表达方法是 Disjoint Set Union，AKA DSU。

基础做法：一树一集合。
路径压缩：均摊复杂度 $Θ (n \log n + q)$ 。

按秩合并：将小子树作为大子树的儿子，维持深度在

O (\log n)

级别。

void merge(int x,int y) {
	int xfa=get(x),yfa=get(y);
	if(xfa==yfa) return;
	if(size[xfa]<size[yfa]) std::swap(xfa,yfa);
	fa[yfa]=xfa,size[xfa]+=size[yfa];//特别注意 fa 和 size 合并方向相反别写错！！！
}

所谓“秩”，即为等级、顺序。按秩合并分为两种：以树的大小为秩和以树的深度为秩。这里我们采用前者。

两者结合：时间复杂度为 $O (n α (n) + q)$ ，其中 $α$ 为反阿克曼函数。

单变量反 Ackermann 函数（简称反 Ackermann 函数） $α (x)$ 定义为最大的整数 $m$ 使得 $A c k e r m a n n (m, m) \leq x$ 。因为 Ackermann 函数的增长很快，所以其反函数 $α (x)$ 的增长是非常慢的，对所有在实际问题中有意义的 $x$ ， $α (x) \leq 4$ ，所以在算法时间复杂度分析等问题中，可以把 $α (x)$ 看成常数。
可撤销：为支持撤销上一个合并操作，我们考虑 抛弃路径压缩，只使用按秩合并，用栈记录合并操作，撤销时删边重新计算子树大小即可。

路径压缩的 $Θ (n \log n + q) a$ 复杂度为均摊，且 改变了树的形态，故会导致对撤销的复杂度无法保证。
Kruskal 重构树：合并根节点 $u, v$ 时，新建节点 $w$ ，将 $u, v$ 作为 $w$ 的儿子，得到的树称为 Kruskal 重构树。可以处理与时间相关的查询问题，常搭配倍增使用。合并时新建的节点 $w$ 带 时间属性，可以搭配倍增求 LCA 支持 可持久化并查集在线查询。

下面是一个 以树的大小按秩合并的可撤销并查集 模板：

struct DSU {
	int fa[N],size[N],top=0;
	struct data { int x,y,xfa,yfa; } s[N];
	void init() { for(int i=1;i<=n;++i) fa[i]=i,size[i]=1; }
	int get(int x) { return fa[x]==x?x:get(fa[x]); }
	void merge(int x,int y) {
		int xfa=get(x),yfa=get(y);
		if(xfa==yfa) return;
		if(size[xfa]<size[yfa]) std::swap(xfa,yfa);
		fa[yfa]=xfa,size[xfa]+=size[yfa],s[++top]={x,y,xfa,yfa};
	}
	void cancel() { fa[s[top].yfa]=s[top].yfa,size[s[top].xfa]-=size[s[top].yfa],--top; }
};

2. 倍增

2.1 树上倍增

2.1.1 LCA 的经典倍增求法

树上倍增最经典的应用是 倍增 LCA 求法，还可以用来维护树上可重复贡献问题。（什么是可重复贡献问题后面有讲到。）

$f (u, i)$ 为节点 $u$ 向上跳 $2^{i}$ 步到达的节点，则有

f (u, i) = f (f (u, i - 1), i - 1),

遍历预处理 $f$ 即可 $O ((n + q) \log n)$ 求 LCA。

void dfs(int x) {
	for(int i=1;i<=20;++i) f[x][i]=f[f[x][i-1]][i-1];
	for(auto i:e[x]) i!=f[x][0]&&(f[i][0]=x,dep[i]=dep[x]+1,dfs(i),0);
}

你可能注意到了在搜索中我们记录了每个节点的深度，这也是很重要的一环。在查询两个点的 LCA 时，大致分为以下几个步骤：

深度深的一点向上跳转至他的祖先节点，直至和另一点深度相同。
深度相同后，两点是同一个节点，则该节点为两点的 LCA。
深度相同后，两点仍不相同，则继续向上跳转至其祖先节点。
如果两个节点的祖先节点相同，则不要跳转，这个祖先节点可能不是两点的最近公共祖先。当两个点的父节点相同时，该父节点是两点的 LCA。

文字说可能比较乏味？那我来个图：

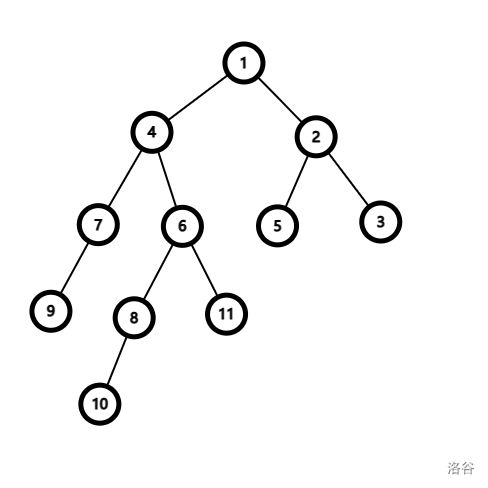
LCA图例

查询 $10$ 和 $2$ 的 LCA，操作步骤如下：

$d e p_{10} > d e p_{2}$ ，深度差 3。开始跳转： $10 \to f a (10, 1) = 6 \to f a (6, 0) = 4$ 。
同深度，节点不同，继续跳转。两点父节点相同，父节点 $1$ 就是 $10$ 和 $2$ 的 LCA。

大概来说就是这样了，下面是代码：

int LCA(int u,int v) {
	if(dep[u]<dep[v]) swap(u,v);//个人习惯，每次都让u的深度更深
	int len=dep[u]-dep[v];
	for(int i=20;i>=0;--i) len&(1<<i)&&(u=f[u][i]);//深度差二进制拆分，跳转
	if(u==v) return u;
	for(int i=20;i>=0;--i) f[u][i]!=f[v][i]&&(u=f[u][i],v=f[v][i]);//只有祖先节点不同才跳
	return f[u][0];
}

2.1.2 冷门科技：dfs 序求 LCA

上面那个东西固然好，但 ~~是答辩了~~ 时代变了。接下来介绍冷门科技 dfs 序的 LCA 求法。

具体讲解可以看魏老师的博客。初代冷门科技就是用 $d e p$ 辅助的 dfs 序倍增。

inline int get(int x,int y) { return dep[x]<dep[y]?x:y; }
void dfs(int u,int fa) {
	f[0][dfn[u]=++tot]=fa,dep[u]=dep[fa]+1;
	for(int p=head[u],v=E[p].to;p;p=E[p].next,v=E[p].to) if(v!=fa) dfs(v,u);
}
void init() {
	lg[0]=-1;
	for(int i=1;i<=tot;++i) lg[i]=lg[i>>1]+1;
	for(int j=1;j<=lg[tot];++j)
		for(int i=1;i+(1<<j)-1<=n;++i)
			f[j][i]=get(f[j-1][i],f[j-1][i+(1<<j-1)]);
}
int LCA(int u,int v) {
	if(u==v) return u;
	if((u=dfn[u])>(v=dfn[v])) std::swap(u,v);
	int d=lg[v-u++];
	return get(f[d][u],f[d][v-(1<<d)+1]);
}

后来人们甚至不满足于这个了。我们发现直接寻找 $d f n$ 最小的正确性仍然成立~~，到现在我都不太知道这是怎么对的啊啊啊~~，反正是对的。嗯，。既然是科技，大不了就 remember it instead of understanding。

// Author: MichaelWong
// Code: C++14(GCC 9)
// Date: 2023/8/21
// File: 【冷门科技】dfs序求LCA.cpp
#include<bits/stdc++.h>
#define ll long long
#define ld long double
#define pii std::pair<int,int>
#define fsp(x) std::fixed<<std::setprecision(x)
#define forE(u) for(int p=head[u],v=to[p];p;p=next[p],v=to[p])
const int N=5e5+5;
int cnt,head[N],next[N<<1],to[N<<1];
inline void add(int u,int v) { to[++cnt]=v,next[cnt]=head[u],head[u]=cnt; }
int n,m,root,tot,dfn[N],lg[N],f[21][N];
inline int get(int x,int y) { return dfn[x]<dfn[y]?x:y; }
void dfs(int u,int fa) {
	f[0][dfn[u]=++tot]=fa;
	forE(u) v^fa&&(dfs(v,u),0);
}
inline void init() {
	lg[0]=-1;
	for(int i=1;i<=n;++i) lg[i]=lg[i>>1]+1;
	for(int i=1;i<=lg[n];++i) for(int j=1;j+(1<<i)-1<=n;++j) f[i][j]=get(f[i-1][j],f[i-1][j+(1<<i-1)]);
}
int lca(int u,int v) {
	if(u==v) return u;
	if((u=dfn[u])>(v=dfn[v])) std::swap(u,v);
	int d=lg[v-u++];
	return get(f[d][u],f[d][v-(1<<d)+1]);
}
int main() {
	std::ios::sync_with_stdio(false);
	std::cin.tie(nullptr); std::cout.tie(nullptr);
	std::cin>>n>>m>>root;
	for(int i=1,u,v;i<n;++i) std::cin>>u>>v,add(u,v),add(v,u);
	dfs(root,0),init();
	for(int i=1,u,v;i<=m;++i) std::cin>>u>>v,std::cout<<lca(u,v)<<'\n';
	return 0;
}
// The code was submitted on Luogu.
// Version: 1.
// If I filled in nothing on the statement,
// it means I'm in a contest and I have no time to do this job.

预处理 ST 表的复杂度仍为 $O (n \log n)$ ，但常数减半。

对比 DFS 序和欧拉序，不仅预处理的时间常数砍半（欧拉序 LCA 的瓶颈恰好在于预处理，DFS 是线性），空间常数也砍半（核心优势），而且还更好写（对于一些题目就不需要再同时求欧拉序和 DFS 序了），也不需要担心忘记开两倍空间，可以说前者从各个方面吊打后者。

对比 DFS 序和倍增，前者单次查询复杂度更优。

对于 DFS 序和四毛子，前者更好写，且单次查询常数更小（其实差不多）。

对于 DFS 序和树剖，前者更好写，且单次查询复杂度更优（但树剖常数较小）。

将 DFS 序求 LCA 发扬光大，让欧拉序求 LCA 成为时代的眼泪！

——Alex_Wei

2.1.3 Kruskal 重构树

上文中我们简单提了一下这个算法，看起来他和 Kruskal 似乎没有一丁点关系，但事实上他们之间也可以有关系。

我们考虑一个 Kruskal 求 MST 的过程，在每次合并两个集合的时候新建一个节点，让合并的两个集合的根成为他的儿子，而他的点权就是 Kruskal 在枚举的这条边的边权，这样我们就得到了一棵 Kruskal 重构树，他具有以下这些性质：

重构树上的叶子结点对应原图中的节点，而其他节点对应着 MST 的边。
Kruskal 枚举的边权从小到大，所以重构树上任意一个节点到根节点的路径上，节点的点权 单调递增。（叶子节点不考虑自身，他没有点权。）
重构树上 $lca (u, v)$ 的点权就是 $u, v$ 在 MST 上的瓶颈，即这一段的最大边权。这是因为 Kruskal 的贪心性质。
重构树本身也是一个 二叉堆。

我们可以通过使用特定关键字排序后进行 Kruskal 的方法，让重构树的节点具有时间或其他属性，再搭配上面的性质，可以解决很多问题，比如下面习题里提到的 NOI2018 的归程。

2.2 ST 表

我必须说明 ST 是 Sparse Table（稀疏表）的缩写，我发现有好多人都不知道它名字的真正来源。

ST 用于解决 RMQ 问题（区间最值问题，Range Minimum / Maximum Query），或者其他 可重复贡献问题。

什么是可重复贡献问题？

举个例子，区间最小值， $min [1, 5] = min (min [1, 4], min [3, 5])$ ，虽然两个区间中 $[3, 4]$ 重合了，但并不影响结果，这就是 可重复贡献。相反，区间和就不是可重复贡献问题，同一个部分不能多次被计算。

可重复贡献问题还要满足 结合律，也就是说运算 $opt$ 的查询是可重复贡献问题，就必须满足：

$(x opt y) opt z = x opt (y opt z)$
RMQ 问题和 $gcd$ 都是可重复贡献问题。

如果是取 $min$ ，则有

m n (u, i) = min (m n (u, i - 1), m n (u + 2^{i - 1}, i - 1)),

$Θ (n \log n)$ 预处理 $m n$ 即可 $O (1)$ 解决 RMQ。

查询 ${min}_{i = l}^{r} {a_{i}}$ 时，令 $d = r - l + 1$ ，直接输出 $min (m n (l, ⌊ \log d ⌋), m n (r - 2^{⌊ \log d ⌋} + 1, ⌊ \log d ⌋))$ 即可，因为可重复贡献问题的两个区间是 可以有交 的。注意 $\log$ 也要 预处理！否则你的查询就变成 $O (\log d_{m a x}) = O (\log n)$ 的啦！

void init() {
	lg[0]=-1;
	for(int i=1;i<=n;++i) lg[i]=lg[i>>1]+1;
	for(int j=1;j<=21;++j) // 21 那里是取决于你的值域最大能到 2 的多少次幂
		for(int i=1;i+(1<<j)-1<=n;++i)
			st[i][j]=std::max(st[i][j-1],st[i+(1<<(j-1))][j-1]);
}
int query(int l,int r) {
	int bit=lg[r-l+1];
	return std::max(st[l][bit],st[r-(1<<bit)+1][bit]);
}

3. 树状数组

用发明人的名字命名为 Fenwick Tree 或按其性质命名为 Binary Indexed Tree，即 二叉索引树，中文也常称为 树状数组，AKA BIT.

BIT 的经典操作是：单点修改，维护前缀，区间查询。

BIT 树结构的构建依靠于 lowbit，这个操作返回一个数字，是输入数字的二进制表示下最小的一位 1 代表的数字，如 $6$ ，二进制表示 110，其 lowbit 是 10(2)，即 2。BIT 树结构的特点是：一个数加上他的 lowbit 是他的父亲，减去他的 lowbit 是他的前驱（兄弟）。

3.1 线性建树

一个小技巧，每个节点更新自己和父亲，顺序是正确的。

inline void build() { for(int i=1;i<=n;++i) t[i]+=a[i],i+lowbit(i)<=n&&(t[i+lowbit(i)]+=t[i]); }

3.2 BIT 上二分

从高到低决定 $x$ 的每一个二进制位是 $0$ 还是 $1$ ，可以给二分降一个 $\log$ ，降成 $O (\log n)$ 。

实际上，BIT 就是省略了右儿子的线段树，因此线段树的功能完全包含 BIT，但为此付出的代价是 $2 \sim 10$ 倍的常数。将 BIT 的树状结构牢记于心，可以更好理解 BIT 倍增. —— Alex Wei

3.3 BIT 维护区间修改

维护差分。注意不是直接维护，这里的维护方法是，维护两个 BIT，分别维护 差分的前缀和 和 $\sum_{i = 1}^{x} i \cdot d i f f_{i}$ ，其中 $d i f f$ 是差分数列。这样一来，在查询时用 $(x + 1)$ 倍前者减去后者，恰巧是 $\sum_{i = 1}^{x} (x - i + 1) d i f f_{i}$ ，而这恰巧是 $\sum_{i = 1}^{x} a_{i}$ 的差分写法。下面是 P3372 【模板】线段树 1 的代码：

// Author: MichaelWong
// Code: C++14(GCC 9)
// Date: 2023/8/21
// File: 【8.21重构】【模板】线段树 1.cpp
#include<bits/stdc++.h>
#define ll long long
#define ld long double
#define pii std::pair<int,int>
#define fsp(x) std::fixed<<std::setprecision(x)
#define forE(u) for(int p=head[u],v=to[p];p;p=next[p],v=to[p])
const int N=1e5+5;
int n,m,a[N],b[N],c[N];
struct BIT {
	ll t[N];
	inline int lowbit(int x) { return x&-x; }
	inline void build(int *src) { for(int i=1;i<=n;++i) t[i]+=src[i],i+lowbit(i)<=n&&(t[i+lowbit(i)]+=t[i]); }
	inline void modify(int x,ll k) { while(x<=n) t[x]+=k,x+=lowbit(x); }
	inline ll query(int x) { ll ans=0; while(x) ans+=t[x],x-=lowbit(x); return ans; }
} t1,t2;
inline void build(int *t1src,int *t2src) { t1.build(t1src),t2.build(t2src); }
inline void modify(int x,ll k) { t1.modify(x,k),t2.modify(x,x*k); }
inline ll query(int x) { return (x+1)*t1.query(x)-t2.query(x); }
inline ll query(int l,int r) { return query(r)-query(l-1); }
int main() {
	std::ios::sync_with_stdio(false);
	std::cin.tie(nullptr); std::cout.tie(nullptr);
	std::cin>>n>>m;
	for(int i=1;i<=n;++i) std::cin>>a[i],b[i]=a[i]-a[i-1],c[i]=i*b[i];
	build(b,c);
	for(int i=1,opt;i<=m;++i) {
		int x,y,k; std::cin>>opt>>x>>y;
		if(opt==1) std::cin>>k,modify(x,k),modify(y+1,-k);
		else std::cout<<query(x,y)<<'\n';
	}
	return 0;
}
// The code was submitted on Luogu.
// Version: 1.
// If I filled in nothing on the statement,
// it means I'm in a contest and I have no time to do this job.

3.4 BIT 维护多维信息

我们可以从上面的区间修改进行推广，如使用四个 BIT 维护二维信息，同样是利用差分的思想，使用

\begin{aligned} A_{x, y} & := \sum_{i = 1}^{x} \sum_{j = 1}^{y} d i f f (i, j), \\ B_{x, y} & := \sum_{i = 1}^{x} \sum_{j = 1}^{y} i \cdot d i f f (i, j), \\ C_{x, y} & := \sum_{i = 1}^{x} \sum_{j = 1}^{y} j \cdot d i f f (i, j), \\ D_{x, y} & := \sum_{i = 1}^{x} \sum_{j = 1}^{y} i \cdot j \cdot d i f f (i, j) . \end{aligned}

分别采用四个树状数组维护，查询时查询 $(x \cdot y + x + y + 1) A_{x, y} - (y + 1) B_{x, y} - (x + 1) C_{x, y} + D_{x, y}$ 即可，这恰好是 $\sum_{i = 1}^{x} \sum_{j = 1}^{y} a (i, j)$ 的差分写法。

struct BIT {
	ll t[N][N];
	inline int lowbit(int x) { return x&-x; }
	inline void modify(int x,int y,ll val) {
		while(x<=n) {
			int nowy=y;
			while(nowy<=n) t[x][nowy]=(t[x][nowy]+val)%mod,nowy+=lowbit(nowy);
			x+=lowbit(x);
		}
	}
	inline ll query(int x,int y) {
		ll ans=0;
		while(x) {
			int nowy=y;
			while(nowy) ans=(ans+t[x][nowy])%mod,nowy-=lowbit(nowy);
			x-=lowbit(x);
		}
		return ans;
	}
} t1,t2,t3,t4;
inline void modify(int x,int y,ll val) { t1.modify(x,y,val),t2.modify(x,y,val*x),t3.modify(x,y,val*y),t4.modify(x,y,val*x*y); }
inline ll query(int x,int y) { return ((((t1.query(x,y)*(x*y+x+y+1)%mod-t2.query(x,y)*(y+1)%mod)%mod-t3.query(x,y)*(x+1)%mod)%mod+t4.query(x,y))%mod+mod)%mod; }

3.5 BIT RMQ

你没听错，BIT 居然还能用来搞 RMQ，方法就是绕过查询时 RMQ 的不可减性，只使用可加性进行操作。具体方法可以看这篇博客，真心觉得不是特别地优雅……挺暴力的，但反正有用就行，复杂度是 $O (\log^{2} n)$ 的，居然能过 ST 表模板题，代码如下。

// Author: MichaelWong
// Code: C++14(GCC 9)
// Date: 2023/8/21
// File: 【模板】ST 表.cpp
#include<bits/stdc++.h>
#define ll long long
#define ld long double
#define pii std::pair<int,int>
#define fsp(x) std::fixed<<std::setprecision(x)
#define forE(u) for(int p=head[u],v=to[p];p;p=next[p],v=to[p])
const int N=1e5+5;
int n,m,a[N],t[N];
inline int lowbit(int x) { return x&-x; }
inline void build() { for(int i=1;i<=n;++i) t[i]=std::max(t[i],a[i]),i+lowbit(i)<=n&&(t[i+lowbit(i)]=std::max(t[i+lowbit(i)],t[i])); }
inline void modify(int x,int k) {
	a[x]=t[x]=k;
	while(x<=n) {
		t[x]=a[x];
		for(int i=1;i<lowbit(x);i<<=1) t[x]=std::max(t[x],t[x-i]);
		x+=lowbit(x);
	}
}
inline int query(int l,int r) {
	int ans=0;
	while(r>=l) {
		if(r-lowbit(r)+1>=l) ans=std::max(ans,t[r]),r-=lowbit(r);
		else ans=std::max(ans,a[r]),--r;
	}
	return ans;
}
int main() {
	std::ios::sync_with_stdio(false);
	std::cin.tie(nullptr); std::cout.tie(nullptr);
	std::cin>>n>>m;
	for(int i=1;i<=n;++i) std::cin>>a[i];
	build();
	for(int i=1,l,r;i<=m;++i) {
		std::cin>>l>>r;
		std::cout<<query(l,r)<<'\n';
	}
	return 0;
}
// The code was submitted on Luogu.
// Version: 1.
// If I filled in nothing on the statement,
// it means I'm in a contest and I have no time to do this job.

- 不是，谁来告诉我，BIT 维护 RMQ 有啥优势啊，md 双 $\log$ 还不好写
- 不好写个 P
- 把 BIT 优雅全丢了，还不如 ST 呢
- 他常数小啊
- 能有 ST 快？
- 他带修啊！
- （思考片刻）窝巢！
所以学一下还是有用的。万一哪天写不完线段树了。

4. 线段树

4.1 基础用法

线段树，顾名思义，我们将一个线段看作一个节点，由这样的无数个节点形成的树，我们称之为 线段树。线段树是常见的 维护区间信息 的数据结构。

直接给图：

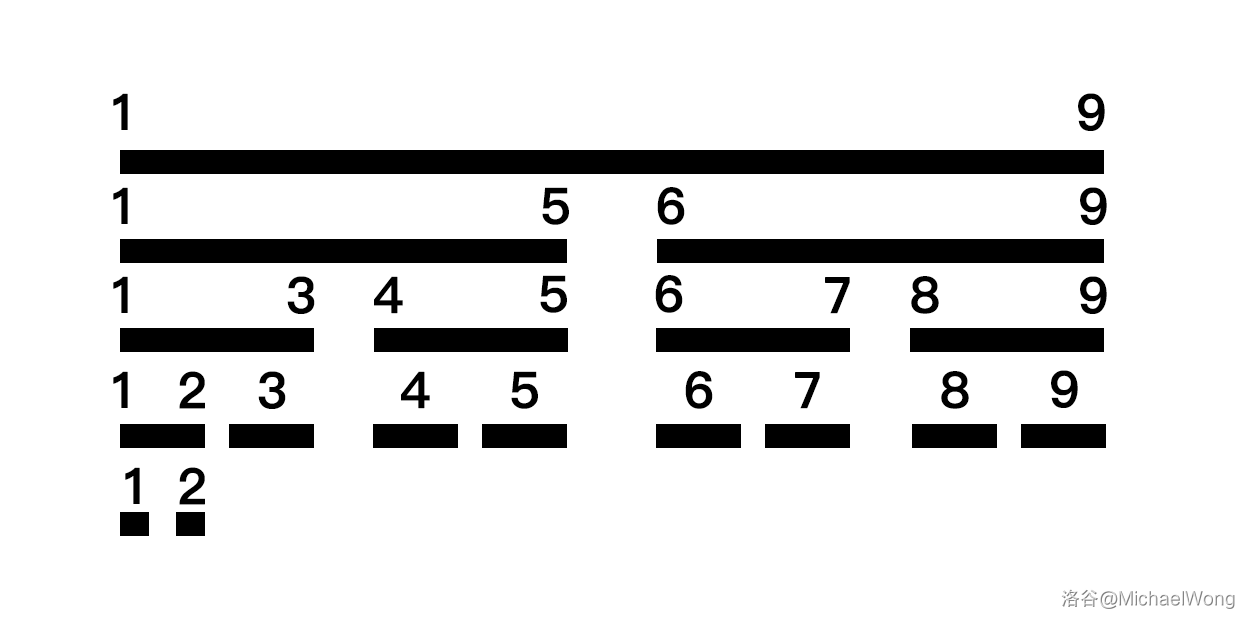
线段树图例

要维护区间 $[1, 9]$ ，生成的线段树就如上图所示。一般来讲，对于元素数量为 $N$ 的区间，生成的线段树的节点数量不会超过 $4 N$ ，所以开数组时开到 $4$ 倍即可。

我们结合 模板题：P3372 【模板】线段树 1 进行讲解。在这道题中，我们需要实现两种操作：

区间加：给定 $l$ , $r$ , $k$ ，将 $[l, r]$ 中的所有元素加上 $k$ 。
区间查询：给定 $l$ , $r$ , $k$ ，查询 $[l, r]$ 中所有元素的和。

线段树是一棵 二叉树。所以按照 BFS 序编号时，节点 $x$ 的两个子节点分别为 $2 x$ 和 $2 x + 1$ （即二进制下的 x>>1 和 x>>1|1），我们可以利用这个性质向下遍历。在书写中，为了方便，我们一般在缺省源中加入这两行：

#define ls x<<1
#define rs x<<1|1

接下来进入线段树的代码部分。

4.1.1 上传 - `pushup`

一般来讲，线段树上层节点信息的维护 极依赖其子节点，所以在每次修改子节点后，我们需要将两个子节点的信息上传到当前节点。如在这里，我们需要维护每个节点的区间和：

void pushup(int x) { sum[x]=sum[ls]+sum[rs]; }

4.1.2 建树 - `build`

我们采用 DFS 的方法建树，预处理每个节点所代表的区间内的所有元素的和 $s u m_{x}$ 。

部分线段树写法会预处理每个节点代表的区间 $[L_{x}, R_{x}],$ 现在我 不建议这么做。因为在后期更复杂的操作中，这多出来的两个数组会占用空间，也会容易导致错误。

代码如下：

void build(int x,int l,int r) { //传参：节点编号，区间边界
	if(l==r) return sum[x]=a[l],void();
	int mid=l+r>>1;
	build(ls,l,mid),build(rs,mid+1,r);
	pushup(x);
}

4.1.3 区间修改（加） - `modify`

大部分平衡树的基础操作，很多进阶题的基本组成部分。

要修改给定的区间 $[l, r]$ 内的所有元素，如果对所要求的区间 $[l, r]$ 中的所有节点都进行修改，时间复杂度无法承受。所以，在线段树中，我们引入了一个新的变量，巧妙的节约了时间，我们通常称这个变量为 懒标记，代码中常写作 lazy。

顾名思义，懒标记是一个非常 “ 懒 ” 的方法——我们用懒标记记录该节点所代表的区间里每一个元素改变的值，在修改一个区间时，我们只修改表示这个区间的节点，并为它打上懒标记，而不向下修改它的孩子们，这样极大地节省了时间。至于它的孩子们，当需要访问他们的时候，我们再将懒标记下传。

有了懒标记，我们只需把要修改的区间拆成尽量少的多个区间，使得在线段树中存在若干个节点直接代表拆开后的区间，并对这些区间进行修改即可。

举个栗子，还是 $[1, 9]$ ，我们建好树后大概就是这个样子：

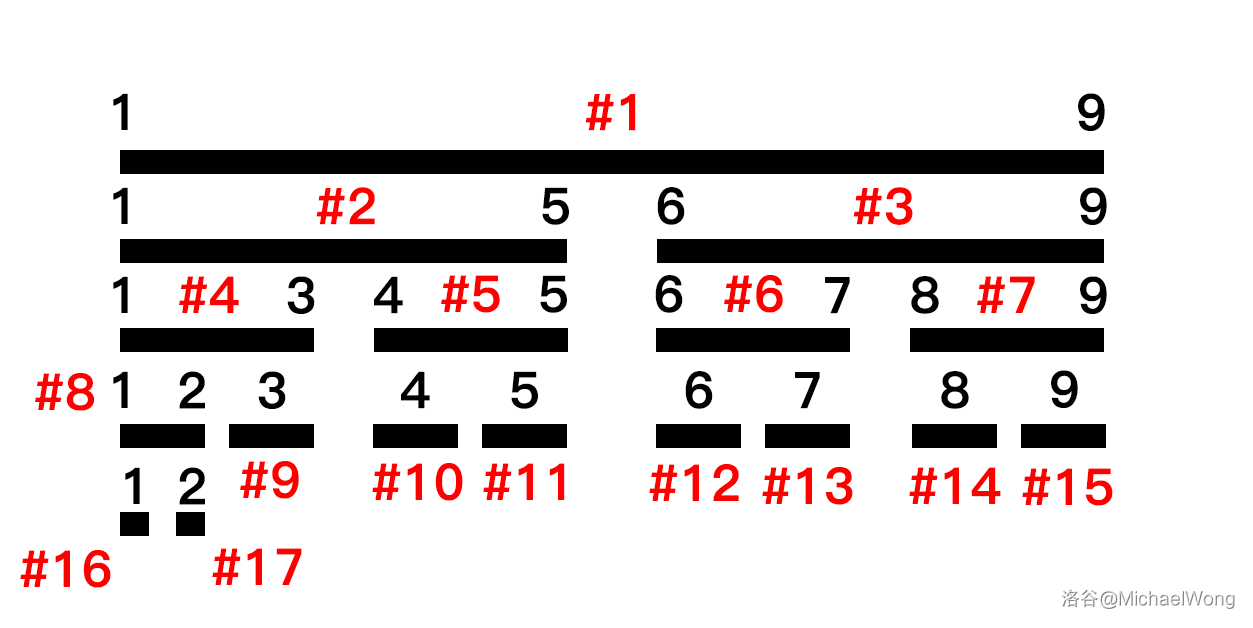
线段树标号

这里我们可以列举几种情况：

如果我们要修改 $[1, 9]$ ，就直接修改 $s u m_{1}$ 和 $l a z y_{1}$ ；
如果是修改 $[1, 3]$ ，就可以通过二分找到 $# 1 \to # 2 \to # 4$ ，然后修改 $s u m_{4}$ 和 $l a z y_{4}$ ；
如果修改 $[5, 8]$ ，则需要拆成多个区间，节点分别为 $# 11$ 、 $# 6$ 、 $# 14$ ，最后修改他们的 $s u m$ 和 $l a z y$ 。

特别注意，当我们访问具有懒标记的节点的子节点时，要现将懒标记下传，否则会影响结果。

代码：

void change(int x,int L,int R,int l,int r,int k) { //当前节点编号，当前所在区间，需要修改的区间，修改的值
	if(l<=L && r>=R) return sum[x]+=(R-L+1)*k,lazy[x]+=k,void(); //当前区间就是要修改的区间
	if(l>R || r<L) return; //当前区间与修改区间不交
	pushdown(x,L,R); //懒标下传
	int M=L+R>>1;
	modify(ls,L,M,l,r,k),modify(rs,M+1,R,l,r,k); //修改子区间
	pushup(x); //上传
}

部分代码中会将修改部分写为：
if(r<=M) modify(ls,L,M,l,r,k);
else if(l>M) modify(rs,M+1,R,l,r,k);
else modify(ls,L,M,l,M,k),modify(rs,M+1,R,M+1,r,k);
这无疑是对的，但是会增加码量，同时对区间匹配错误的情况没有保护措施，容易产生 RE 或死循环，所以 不建议这么写。

4.1.4 懒标下传 - `pushdown`

刚才我们已经介绍了懒标记，简单来说，懒标记帮我们把多次操作记录下来，在向下访问的时候一起下传修改。所以，懒标下传至关重要。

因为非常简单，我就直接上代码了：

void pushdown(int x,int l,int r) //将x节点的懒标记下传
{
	int mid=l+r>>1;
	sum[ls]+=(mid-l+1)*lazy[x],sum[rs]+=(r-mid)*lazy[x];
	lazy[ls]+=lazy[x],lazy[rs]+=lazy[x],lazy[x]=0;
}

当然，如果你记录了区间范围，那么这部分会显得容易些：

void pushdown(int x,int l,int r) { //将x节点的懒标记下传
	int mid=l+r>>1;
	sum[ls]+=(mid-l+1)*lazy[x],sum[rs]+=(r-mid)*lazy[x];
	lazy[ls]+=lazy[x],lazy[rs]+=lazy[x],lazy[x]=0;
}

下传时，只下传一层即可，下传多层同样会浪费时间。

4.1.5 区间查询 - `query`

与区间修改相同，对于给定的区间 $[l, r]$ ，我们把它拆成尽量少的多个区间，使得在线段树中存在若干个节点直接代表拆开后的区间，并对这些区间进行查询，最后输出这些区间查询值的和。

在查询时，如果访问了具有懒标记的节点的子节点，也要记得下传。

代码如下：

long long query(int x,int L,int R,int l,int r) {
	int M=L+R>>1;
	if(l<=L && r>=R) return sum[x];
	if(l>R || r<L) return 0;
	pushdown(x,L,R);
	return query(ls,L,M,l,r)+query(rs,M+1,R,l,r);
}

4.1.6 多个懒标

上面的内容已经足以通过模板题：P3372 【模板】线段树 1 了，我们继续结合模板题：P3373 【模板】线段树 2 讲解一下进阶的操作

在这道题中，我们需要一种新的操作：区间乘。

有聪明的同学可能要说了：我们也像加法一样，为乘法准备一个 独立的懒标记和下传函数 不就可以了吗？

但是，这两个懒标记之间毫无关系吗？显然不是的。

经过简单的推论，我们可以得出：

进行区间乘时，该节点的加法和乘法懒标记 也要同时 进行乘法。
两个懒标记必须 同时下传。
在下传时，子节点的加法和乘法懒标记 都要进行乘法。
传递的顺序应该是 先乘后加。

所以，在同时存在多个修改操作时，必须注意各个懒标记之间的联系。

还要注意，乘法懒标记的初始值应为 1。

$AC CODE$ here

4.2 扫描线

其实扫描线是一个思路，也不一定要通过线段树来实现。~~比如 wcy 硬垒就是一种用途比较广泛的思路。~~

扫描线的思想顾名思义，用一条基准线在图上按照一定顺序扫过，扫描的过程中，每前进一步就处理该基准线上的信息。这样相当于把二维降为了一维，通过扫描维护第二维信息。正因为常见的情况是要维护一条线上的信息，所以才萌生了扫描线 + 线段树的经典搭配——众所周知，线段树是处理区间信息的好工具。

扫描线模板题要求的是矩形的面积并，我们就可以考虑对 $y$ 轴进行扫描，然后维护 $x$ 轴的截线段长度。具体过程不再赘述，可以参考题解，这里附上代码：

// Author: MichaelWong
// Code: C++14(GCC 9)
// Date: 2023/8/23
// File: 扫描线.cpp
#include<bits/stdc++.h>
#define ll long long
#define ld long double
#define int ll // 摆烂行为
#define ls x<<1
#define rs x<<1|1
#define pii std::pair<int,int>
#define fsp(x) std::fixed<<std::setprecision(x)
#define forE(u) for(int p=head[u],v=to[p];p;p=next[p],v=to[p])
const int N=2e5+5;
struct interval { int l,r,y,val; } itv[N<<1];
int n,ans,ax[N],ay[N],bx[N],by[N],sum[N<<2],len[N<<2],xcd[N<<1],xcnt;
inline void pushup(int x,int L,int R) { sum[x]?len[x]=xcd[R+1]-xcd[L]:len[x]=len[ls]+len[rs]; }
void modify(int x,int L,int R,int l,int r,int val) {
	if(R<l||r<L) return;
	if(l<=L&&R<=r) return sum[x]+=val,pushup(x,L,R);
	int M=L+R>>1;
	modify(ls,L,M,l,r,val),modify(rs,M+1,R,l,r,val);
	pushup(x,L,R);
}
signed main() {
	std::ios::sync_with_stdio(false);
	std::cin.tie(nullptr); std::cout.tie(nullptr);
	std::cin>>n;
	for(int i=1;i<=n;++i) std::cin>>ax[i]>>ay[i]>>bx[i]>>by[i],xcd[++xcnt]=ax[i],xcd[++xcnt]=bx[i];
	std::sort(xcd+1,xcd+xcnt+1),xcnt=std::unique(xcd+1,xcd+xcnt+1)-xcd-1;
	for(int i=1;i<=n;++i) {
		ax[i]=std::lower_bound(xcd+1,xcd+xcnt+1,ax[i])-xcd,bx[i]=std::lower_bound(xcd+1,xcd+xcnt+1,bx[i])-xcd;
		itv[i*2-1]={ax[i],bx[i],ay[i],1},itv[i*2]={ax[i],bx[i],by[i],-1};
	}
	std::sort(itv+1,itv+n*2+1,[](const interval &a,const interval &b){ return a.y<b.y; });
	for(int i=1;i<n<<1;++i) modify(1,1,xcnt,itv[i].l,itv[i].r-1,itv[i].val),ans+=len[1]*(itv[i+1].y-itv[i].y);
	std::cout<<ans<<'\n';
	return 0;
}
// The code was submitted on Luogu.
// Version: 1.
// If I filled in nothing on the statement,
// it means I'm in a contest and I have no time to do this job.

用类似的思路还可以求矩形的周长并。~~太墨迹了我就不多说了。~~

5. 习题

I. P1955 [NOI2015] 程序自动分析

并查集板子。把约束条件是相等的变量归入同一个集合，最后判断约束条件是不等的两个变量是否有在同一集合中的情况即可。

II. P6619 [省选联考 2020 A/B 卷] 冰火战士

一道经典的 BIT 上二分 题目。可以详见魏老师博客中的讲解。

#include<bits/stdc++.h>
#define ll long long
#define ld long double
#define fsp(x) std::fixed<<std::setprecision(x)
#define forE(u) for(int p=head[u],v=E[p].to;p;p=E[p].next,v=E[p].to)
const int N=2e6+6;
inline int lowbit(int x) { return x&-x; }
struct data { int opt,t,x,y; } dat[N];
int n,q,cnt,sum,num[N];
struct BIT {
	int sum[N];
	inline void modify(int x,int k) { while(x<=cnt) sum[x]+=k,x+=lowbit(x); }
	inline int query(int x) { int ans=0; while(x) ans+=sum[x],x-=lowbit(x); return ans; }
} t[2];
void query() {
	int ans0,ans1,pos0,pos=0,sum0=0,sum1=sum;
	for(int i=20;~i;--i) {
		int now=pos+(1<<i),s0=sum0+t[0].sum[now],s1=sum1-t[1].sum[now];
		if(now>cnt) continue;
		if(s0<s1) pos=now,sum0=s0,sum1=s1;
	}
	ans0=sum0,pos0=pos,pos=0,sum0=0,sum1=sum;
	if(pos0<cnt) {
		ans1=sum-t[1].query(pos0+1);
		for(int i=20;~i;--i) {
			int now=pos+(1<<i),s0=sum0+t[0].sum[now],s1=sum1-t[1].sum[now];
			if(now>cnt) continue;
			if(s0<s1||std::min(s0,s1)==ans1) pos=now,sum0=s0,sum1=s1;
		}
	}
	if(std::max(ans0,ans1)==0) std::cout<<"Peace\n";
	else if(ans1<ans0) std::cout<<num[pos0]<<' '<<(ans0<<1)<<'\n';
	else std::cout<<num[pos]<<' '<<(ans1<<1)<<'\n';
}
int main() {
	std::ios::sync_with_stdio(false);
	std::cin.tie(nullptr); std::cout.tie(nullptr);
	std::cin>>q;
	for(int i=1;i<=q;++i) {
		std::cin>>dat[i].opt>>dat[i].t;
		if(dat[i].opt==1) std::cin>>dat[i].x>>dat[i].y,num[++cnt]=dat[i].x;
	}
	std::sort(num+1,num+cnt+1),cnt=std::unique(num+1,num+cnt+1)-num-1;
	for(int i=1;i<=q;++i) {
		if(dat[i].opt==1) {
			dat[i].x=std::lower_bound(num+1,num+cnt+1,dat[i].x)-num;
			t[dat[i].t].modify(dat[i].x+dat[i].t,dat[i].y);
			dat[i].t&&(sum+=dat[i].y);
		}
		else {
			int pos=dat[i].t;
			t[dat[pos].t].modify(dat[pos].x+dat[pos].t,-dat[pos].y);
			dat[pos].t&&(sum-=dat[pos].y);
		}
		query();
	}
	return 0;
}

III. P3295 [SCOI2016] 萌萌哒

对应的是一类很常见的思路——使用并查集维护 连通性。一种常见的维护方法是使用并查集维护 当前连通块的终点，可以参考 P2391 白雪皑皑这道题；另一种常见的维护方法将连通的部分 merge 进同一个集合。这道题表示如此，同时采用了倍增的思想，使用 $f a (i, k)$ 表示 $[i, i + 2^{k} - 1]$ 这一段连通块所在的集合，然后先倍增差分区间，merge 满足约束，然后对于每个节点 $k$ 从高到低 merge 即可，最后查询 $f a (i, 0)$ 是否为本身，显然只有是本身的时候可以自由填数。

#include<bits/stdc++.h>
#define ll long long
const int N=1e5+5,mod=1e9+7;
int n,m,fa[N][20],ans;
int get(int x,int k) {return fa[x][k]==x?x:fa[x][k]=get(fa[x][k],k);}
void merge(int x,int y,int k) {fa[get(x,k)][k]=get(y,k);}
int main() {
	std::ios::sync_with_stdio(false);
	std::cin.tie(nullptr);std::cout.tie(nullptr);
	std::cin>>n>>m;
	for(int i=1;i<=n;++i) for(int k=0;k<=18;++k) fa[i][k]=i;
	for(int i=1;i<=m;++i) {
		int l1,r1,l2,r2,k;
		std::cin>>l1>>r1>>l2>>r2;
		for(int k=18;~k;--k)
			if(l1+(1<<k)-1<=r1) merge(l1,l2,k),l1+=1<<k,l2+=1<<k;
	}
	for(int k=18;k;--k) {
		for(int i=1;i+(1<<k)-1<=n;++i) {
			int f=get(i,k);
			merge(i,f,k-1),merge(i+(1<<k-1),f+(1<<k-1),k-1);
		}
	}
	for(int i=1;i<=n;++i)
		if(fa[i][0]==i) ans=!ans?9:(ll)ans*10%mod;
	std::cout<<ans;
	return 0;
}

IV. P5280 [ZJOI2019] 线段树

一道线段树上 DP，主要思路是将线段树上的节点分类讨论，分别求出状态转移方程，然后在一棵线段树上模拟操作过程。

// Author: MichaelWong
// Code: C++14(GCC 9)
// Date: 2023/8/22
// File: P5280 [ZJOI2019] 线段树.cpp
#include<bits/stdc++.h>
#define ll long long
#define ld long double
#define ls (x<<1)
#define rs (x<<1|1)
#define pii std::pair<int,int>
#define fsp(x) std::fixed<<std::setprecision(x)
#define forE(u) for(int p=head[u],v=to[p];p;p=next[p],v=to[p])
const int N=1e5+5,mod=998244353;
int n,m;
class modint {
	private:
		int value;
	public:
		modint(int x=0) { while(x>mod) x-=mod; value=x; }
		modint(const modint &x)=default;
		modint operator+ (const modint &x) { modint ans=value+x.value; ans.value>=mod&&(ans.value-=mod); return ans; }
		modint operator- (const modint &x) { modint ans=value-x.value; ans.value<0&&(ans.value+=mod); return ans; }
		modint operator* (const modint &x) { modint ans=1ll*value*x.value%mod; return ans; }
		modint operator& (const modint &x) { modint ans=value&x.value; return ans; }
		modint operator& (const int &x) { modint ans=value&x; return ans; }
		modint operator^ (const modint &x) { modint ans=value^x.value; return ans; }
		modint operator^ (const int &x) { modint ans=value^x; return ans; }
		modint operator>> (const modint &x) { modint ans=value>>x.value; return ans; }
		modint operator<< (modint x) {
			modint ans=1,base=2;
			while(x) {
				x&1&&(ans*=base);
				base*=base,x>>=1;
			}
			return *this*ans;
		}
		modint& operator= (int x) { while(x>mod) x-=mod; value=x; return *this; }
		modint& operator+= (const modint &x) { return *this=*this+x; }
		modint& operator*= (const modint &x) { return *this=*this*x; }
		modint& operator>>= (const modint &x) { return *this=*this>>x; }
		modint& operator<<= (const modint &x) { return *this=*this<<x; }
		modint operator++ () { ++value>=mod&&(value-=mod); return *this; }
		operator int() const { return value; }
} BLN=1,f[N<<3],g[N<<3],sum[N<<3],flz[N<<3],glz[N<<3];
inline void pushup(int x) { sum[x]=f[x]+sum[ls]+sum[rs]; }
inline void pushcs3(int x) { f[x]+=BLN-g[x],g[x]<<=1; }
inline void pushf(int x,modint val=2) { f[x]*=val,flz[x]*=val,sum[x]*=val; }
inline void pushg(int x,modint val=2) { g[x]*=val,glz[x]*=val; }
inline void pushdown(int x) {
	flz[x]^1&&(pushf(ls,flz[x]),pushf(rs,flz[x]),flz[x]=1);
	glz[x]^1&&(pushg(ls,glz[x]),pushg(rs,glz[x]),glz[x]=1);
}
void build(int x,int l,int r) {
	f[x]=0,g[x]=1,flz[x]=glz[x]=1;
	if(l==r) return;
	int mid=l+r>>1;
	build(ls,l,mid),build(rs,mid+1,r);
}
void modify(int x,int L,int R,int l,int r) {
	pushdown(x);
	if(L==l&&R==r) return f[x]+=BLN,pushf(ls),pushf(rs),pushup(x);
	int M=L+R>>1; g[x]+=BLN;
	if(r<=M) modify(ls,L,M,l,r),pushdown(rs),pushcs3(rs),pushf(rs<<1),pushf(rs<<1|1),pushg(rs<<1),pushg(rs<<1|1),pushup(rs);
	else if(l>M) modify(rs,M+1,R,l,r),pushdown(ls),pushcs3(ls),pushf(ls<<1),pushf(ls<<1|1),pushg(ls<<1),pushg(ls<<1|1),pushup(ls);
	else modify(ls,L,M,l,M),modify(rs,M+1,R,M+1,r);
	pushup(x);
}
int main() {
	std::ios::sync_with_stdio(false);
	std::cin.tie(nullptr); std::cout.tie(nullptr);
	std::cin>>n>>m; build(1,1,n);
	for(int i=1,opt,l,r;i<=m;++i) {
		std::cin>>opt;
		if(opt==1) std::cin>>l>>r,modify(1,1,n,l,r),BLN<<=1;
		else std::cout<<sum[1]<<'\n';
	}
	return 0;
}
// The code was submitted on Luogu.
// Version: 1.
// If I filled in nothing on the statement,
// it means I'm in a contest and I have no time to do this job.

V. CF891C Envy

考察对 MST 算法理解的题。在 Kruskal 生成 MST 的过程中，我们不难得出，同样权值的边组成的集合只存在两种情况：

全部归入 MST 中
部分（全部）未归入 MST 中

后者只能是因为权值 小于等于 当前权值的一些边组成的边集连通了未归入边的两个端点。而如果我们钦定在这个集合中当前边永远被优先考虑，则只能是小于的情况了。所以我们可以得出推论：

当 Kruskal 将小于固定权值的边全部考虑结束后，对于所有正确的方案，图的连通性相同。

其实这简单反证就能证出来，以至于题解第二篇赞其为废话 hhhh。

所以这道题的思路就很清晰了，根据边权一层一层来。对于每一层，枚举一个优先考虑的边集，考虑将这个边集中这一层边权的边全部加入生成树中，如果不可以则该边集不合法；否则，还原到这一层的初始状态（即小于该层边权的边全部考虑，等于该层边权的边都未考虑），继续枚举下一个优先考虑的边集即可；所有边集枚举结束后，进入下一层，Kruskal 继续推进到把当前层边权的边都考虑后即可。

所以这道题就是 Kruskal + 可撤销并查集，可撤销是为了还原到每一层的初始状态，根据第一部分的讲解，我们考虑采用按秩合并，用栈记录操作。

#include<bits/stdc++.h>
#define ll long long
#define ld long double
#define fsp(x) std::fixed<<std::setprecision(x)
#define forE(u) for(int p=head[u],v=E[p].to;p;p=E[p].next,v=E[p].to)
const int N=5e5+5;
int n,m,q,x[N],y[N],w[N],tmp[N],ans[N],cnt=0,cur=1;
std::vector<int> que[N];
namespace DSU {
	int fa[N],size[N],top=0;
	struct data { int x,y,xfa,yfa; } s[N];
	void init() { for(int i=1;i<=n;++i) fa[i]=i,size[i]=1; }
	int get(int x) { return fa[x]==x?x:get(fa[x]); }
	void merge(int x,int y) {
		int xfa=get(x),yfa=get(y);
		if(xfa==yfa) return;
		if(size[xfa]<size[yfa]) std::swap(xfa,yfa);
		fa[yfa]=xfa,size[xfa]+=size[yfa],s[++top]={x,y,xfa,yfa};
	}
	bool check(int x,int y) { return top&&s[top].x==x&&s[top].y==y; }
	void cancel() { fa[s[top].yfa]=s[top].yfa,size[s[top].xfa]-=size[s[top].yfa],--top; }
}
using namespace DSU;
struct edge {
	int from,to,w;
	bool operator< (const edge &x) { return w<x.w; }
} E[N];
int main() {
	std::ios::sync_with_stdio(false);
	std::cin.tie(nullptr); std::cout.tie(nullptr);
	std::cin>>n>>m; init();
	for(int i=1;i<=m;++i) std::cin>>x[i]>>y[i]>>w[i],E[i].from=x[i],E[i].to=y[i],E[i].w=w[i];
	std::sort(E+1,E+m+1);
	std::cin>>q;
	for(int i=1;i<=q;++i) {
		int k; std::cin>>k; ans[i]=1;
		for(int j=1;j<=k;++j) std::cin>>tmp[j];
		std::sort(tmp+1,tmp+k+1,[](int x,int y){ return w[x]<w[y]; });
		for(int j=1;j<=k;++j) {
			if(w[tmp[j-1]]!=w[tmp[j]]) que[++cnt].push_back(i);
			que[cnt].push_back(tmp[j]);
		}
	}
	std::sort(que+1,que+cnt+1,[](const std::vector<int> &x,const std::vector<int> &y){ return w[x[1]]<w[y[1]]; });
	for(int i=1;i<=cnt;++i) {
		bool flag=1;
		while(cur<=m&&E[cur].w<w[que[i][1]]) { merge(E[cur].from,E[cur].to),++cur; }
		for(int j=1;j<que[i].size();++j) { int tmp=que[i][j]; if(get(x[tmp])==get(y[tmp])) flag=0; else merge(x[tmp],y[tmp]); }
		for(int j=que[i].size()-1;j;--j) { int tmp=que[i][j]; if(check(x[tmp],y[tmp])) cancel(); }
		ans[que[i][0]]&=flag;
	}
	for(int i=1;i<=q;++i) std::cout<<(ans[i]?"YES":"NO")<<'\n';
	return 0;
}

VI. P4768 [NOI2018] 归程

一道非常巧妙的题。

考虑每个点到 $1$ 的距离，这很容易通过最短路算法求出，问题就在于找到出发点所在连通块到 $1$ 的最短距离，换言之，快速求出出发点所在的连通块内 $min_{i} {d i s_{i}}$ 是本题的瓶颈所在。

如果使用诸如 Tarjan 缩点一类算法，则无法很好的应对在线多次查询，因为每次断边都不同。我们考虑采用 Kruskal 重构树，将道路的海拔 $a$ 作为边权生成一棵 MST。这样，我们就可以通过重构树快速找到连通块了——我们找出发点 $v$ 所在的子树，当子树的根 $u$ 满足 $a_{u} > p$ 且 $a_{f a_{u}} < p$ 的时候，以 $u$ 为根的子树的所有叶子结点就是 $v$ 所在的连通块的所有节点了，取他们的 $d i s$ 的最小值即可。

因此，我们先 dijkstra 求出单源最短路长度，然后以海拔为关键字从大到小排序（目的是让根结点的海拔最大），建立 Kruskal 重构树，通过 dfs 求出每棵子树的 $d i s$ 最小值，在查询的时候倍增跳父亲就可以快速找到我们要的祖先了，本题解毕。

// Author: MichaelWong
// Code: C++14(GCC 9)
// Date: 2023/8/24
// File: P4768 [NOI2018] 归程.cpp
// This is absolutely an epic code for me.
#include<bits/stdc++.h>
#define ll long long
#define ld long double
#define fr first
#define sc second
#define pii std::pair<int,int>
#define fsp(x) std::fixed<<std::setprecision(x)
#define forE(u) for(int p=head[u],v=to[p];p;p=next[p],v=to[p])
const int N=2e5+5,M=4e5+5;
int n,m,lastans,T,Q,K,S,v,p;
bool flag[N];
int fa[N<<1],f[20][N<<1],dis[N],tot,MST_edge_cnt;
struct edge { int from,to,h; } E[M];
int cnt,head[N<<1],w[M<<2],to[M<<2],next[M<<2];
inline void add(int u,int v,int w=0) { to[++cnt]=v,::w[cnt]=w,next[cnt]=head[u],head[u]=cnt; }
inline void graph_init() { cnt=1,memset(head,0,sizeof head); }
struct node { int w,h; } nd[N<<1];
inline void add(int u,int v,int w,int h,int id) { add(u,v,w),add(v,u,w),E[id].from=u,E[id].to=v,E[id].h=h; }
inline void init() {
	lastans=0; graph_init();
	for(int i=1;i<=n<<1;++i) fa[i]=i;
	MST_edge_cnt=0,tot=n,memset(f,0,sizeof f);
}
inline void decode(int &v,int &p) { v=(v+K*lastans-1)%n+1,p=(p+K*lastans)%(S+1); }
int get(int x) { return fa[x]==x?x:fa[x]=get(fa[x]); }
inline void merge(int x,int y,int h) {
	int xfa=get(x),yfa=get(y);
	fa[xfa]=fa[yfa]=++tot;
	add(tot,xfa),add(tot,yfa);
	nd[tot].h=h;
}
inline void dijkstra() {
	memset(dis,0x3f,sizeof dis);
	memset(flag,0,sizeof flag);
	std::priority_queue<pii,std::vector<pii>,std::greater<pii>> q;
	q.push({dis[1]=0,1});
	while(!q.empty()) {
		auto u=q.top(); q.pop();
		if(flag[u.sc]) continue; flag[u.sc]=1;
		forE(u.sc) dis[v]>dis[u.sc]+w[p]&&(q.push({dis[v]=dis[u.sc]+w[p],v}),0);
	}
	for(int i=1;i<=n;++i) nd[i].w=dis[i];
	for(int i=n+1;i<=n<<1;++i) nd[i].w=0x3f3f3f3f;
}
inline void kruskal() {
	graph_init();
	std::sort(E+1,E+m+1,[](const edge &a,const edge &b){ return a.h>b.h; });
	for(int i=1;i<=m;++i) {
		int u=E[i].from,v=E[i].to;
		if(get(u)==get(v)) continue;
		merge(u,v,E[i].h);
		if(++MST_edge_cnt==n-1) break;
	}
}
void dfs(int u,int father) {
	f[0][u]=father;
	for(int i=1;i<=19;++i) f[i][u]=f[i-1][f[i-1][u]];
	forE(u) dfs(v,u),nd[u].w=std::min(nd[u].w,nd[v].w);
}
inline int query(int v,int p) {
	for(int i=19;~i;--i) (f[i][v]&&nd[f[i][v]].h>p)&&(v=f[i][v]);
	return lastans=nd[v].w;
}
int main() {
	std::ios::sync_with_stdio(false);
	std::cin.tie(nullptr); std::cout.tie(nullptr);
	std::cin>>T;
	while(T--) {
		std::cin>>n>>m; init();
		for(int i=1,u,v,w,h;i<=m;++i) std::cin>>u>>v>>w>>h,add(u,v,w,h,i);
		dijkstra(),kruskal(),dfs(tot,0);
		std::cin>>Q>>K>>S;
		for(int i=1;i<=Q;++i) {
			std::cin>>v>>p; decode(v,p);
			std::cout<<query(v,p)<<'\n';
		}
	}
	return 0;
}
// The code was submitted on Luogu.
// Version: 1.
// If I filled in nothing on the statement,
// it means I'm in a contest and I have no time to do this job.

7.18 - 数据结构扩展

1. 线段树合并

1.1 动态开点线段树

这是线段树合并的基础。

当我拿出这个数据范围，阁下又如何应对：

$0 \leq a_{i} \leq 10^{9} .$
如果你需要一个值域线段树，那总不能开 $N = 1 e 9$ 的数组，更何况线段树是 $4 N$ 。现在晓得 动态开点 的重要性了吧。

抛弃那个 提前开点独占 的 x<<1 和 x<<1|1，使用 $l s_{x}$ 和 $r s_{x}$ 记录 $x$ 的左儿子和右儿子， $n o d e$ 记录节点总数。动态开点就别再使用懒标啦，容易出事。你只需要：

void change(int l,int r,int p,int &x,int v) {
	if(!x) x=++node; val[x]+=v；
	if(l==r) return;
	int mid=l+r>>1;
	if(p<=mid) change(l,mid,p,ls[x],v);
	else change(mid+1,r,p,rs[x],v);
}
int query(int x,int L,int R,int l,int r) {
	if(l<=L && r>=R) return sum[x];
	if(l>R || r<L || !x) return 0;
	int M=L+R>>1,ans=0;
	ans+=query(ls[x],L,M,l,r)+query(rs[x],M+1,R,l,r);
	return ans;
}

差不多就是这个意思，有时候可以用 pushup，有时候则需要沿途更新所有节点信息，看哪个更方便更好实现吧。

1.2 线段树合并

P4556 【模板】线段树合并代码：

#include<bits/stdc++.h>
#define ll long long
const int N=1e5+5;
int n,m;
int cnt,head[N];
struct edge { int to,next; } E[N<<1];
void add(int u,int v) { E[++cnt].to=v,E[cnt].next=head[u],head[u]=cnt; }
//dfs & lca module
int tot,dep[N],dfn[N],f[20][N],fa[N],lg[N];
int get(int x,int y) { return dep[x]<dep[y]?x:y; }
void dfs(int u,int father) {
	f[0][dfn[u]=++tot]=father,dep[u]=dep[fa[u]=father]+1;
	for(int p=head[u],v=E[p].to;p;p=E[p].next,v=E[p].to) if(v!=father) dfs(v,u);
}
void init() {
	lg[0]=-1;
	for(int i=1;i<=tot;++i) lg[i]=lg[i>>1]+1;
	for(int j=1;j<=lg[tot];++j)
		for(int i=1;i+(1<<j)-1<=n;++i)
			f[j][i]=get(f[j-1][i],f[j-1][i+(1<<j-1)]);
}
int LCA(int u,int v) {
	if(u==v) return u;
	if((u=dfn[u])>(v=dfn[v])) std::swap(u,v);
	int d=lg[v-u++];
	return get(f[d][u],f[d][v-(1<<d)+1]);
}
//segment_tree module
int node,ls[N<<6],rs[N<<6],val[N<<6],mx[N<<6];
void pushup(int x) {
	val[x]=std::max(val[ls[x]],val[rs[x]]);
	mx[x]=val[x]==val[ls[x]]?mx[ls[x]]:mx[rs[x]];
}
void pushup(int x,int y,int z) { val[z]=val[x]+val[y],mx[z]=mx[x]; }
void change(int l,int r,int p,int &x,int v) {
	if(!x) x=++node;
	if(l==r) return val[x]+=v,mx[x]=p,void();
	int mid=(l+r)>>1;
	if(p<=mid) change(l,mid,p,ls[x],v);
	else change(mid+1,r,p,rs[x],v);
	pushup(x);
}
void merge(int l,int r,int x,int y,int &z) {
	if(!x||!y) return z=x|y,void();
	int mid=(l+r)>>1;
	if(l==r) return pushup(x,y,z);
	merge(l,mid,ls[x],ls[y],ls[z]);
	merge(mid+1,r,rs[x],rs[y],rs[z]);
	return pushup(z);
}
//second dfs module
int rt[N],ans[N];
void NB_dfs(int u) {
	for(int p=head[u],v=E[p].to;p;p=E[p].next,v=E[p].to) if(v!=fa[u]) NB_dfs(v),merge(1,N,rt[u],rt[v],rt[u]);
	ans[u]=val[rt[u]]?mx[rt[u]]:0;
}
//main
int main() {
	std::ios::sync_with_stdio(false);
	std::cin.tie(nullptr); std::cout.tie(nullptr);
	std::cin>>n>>m;
	for(int i=1,a,b;i<n;++i) {
		std::cin>>a>>b;
		add(a,b),add(b,a);
	}
	dfs(1,0),init();
	for(int i=1;i<=m;++i) {
		int x,y,z; std::cin>>x>>y>>z; int lca=LCA(x,y);
		change(1,N,z,rt[x],1);
		change(1,N,z,rt[y],1);
		change(1,N,z,rt[lca],-1);
		if(fa[lca]) change(1,N,z,rt[fa[lca]],-1);
	}
	NB_dfs(1);
	for(int i=1;i<=n;++i) std::cout<<ans[i]<<'\n';
	return 0;
}

2. 李超线段树

解决比如这种问题。

具体如何做呢？

当给定一个线段的时候，我们求其解析式。

void analyze(int ax,int ay,int bx,int by) {
	++cnt;
	if(ax==bx) l[cnt].k=0,l[cnt].b=std::max(ay,by); // 特判平行 y 轴直线
	else l[cnt].k=(ld)(by-ay)/(bx-ax),l[cnt].b=ay-l[cnt].k*ax;
}

特别注意的是，平行于 $y$ 轴的直线认为一次项系数为 $0$ 。

接下来，对其值域，也就是线段所覆盖的 $x$ 轴的区间进行修改。

void modify(int x,int L,int R,int l,int r,int id) { // 这个函数用来找到值域对应的节点
	if(l<=L&&R<=r) return cover(x,L,R,id);
	int M=L+R>>1;
	if(l<=M) modify(ls,L,M,l,r,id);
	if(M<r) modify(rs,M+1,R,l,r,id);
}

如何在旧的线段和新的线段之间选择呢？我们认为当前节点表示的区间的中点对应 $y$ 坐标高的线段就是 该区间的最优线段。

确定当前区间的最优线段之后，考虑到两个直线可能在区间内相交，也就是说这条直线 并不是 区间内所有点的最优解，再对左右端点进行判断，如果出现当前线段比最优线段高，那么递归地去更新子节点的最优线段。当前区间的最优线段始终是中点最高的。

李超图解

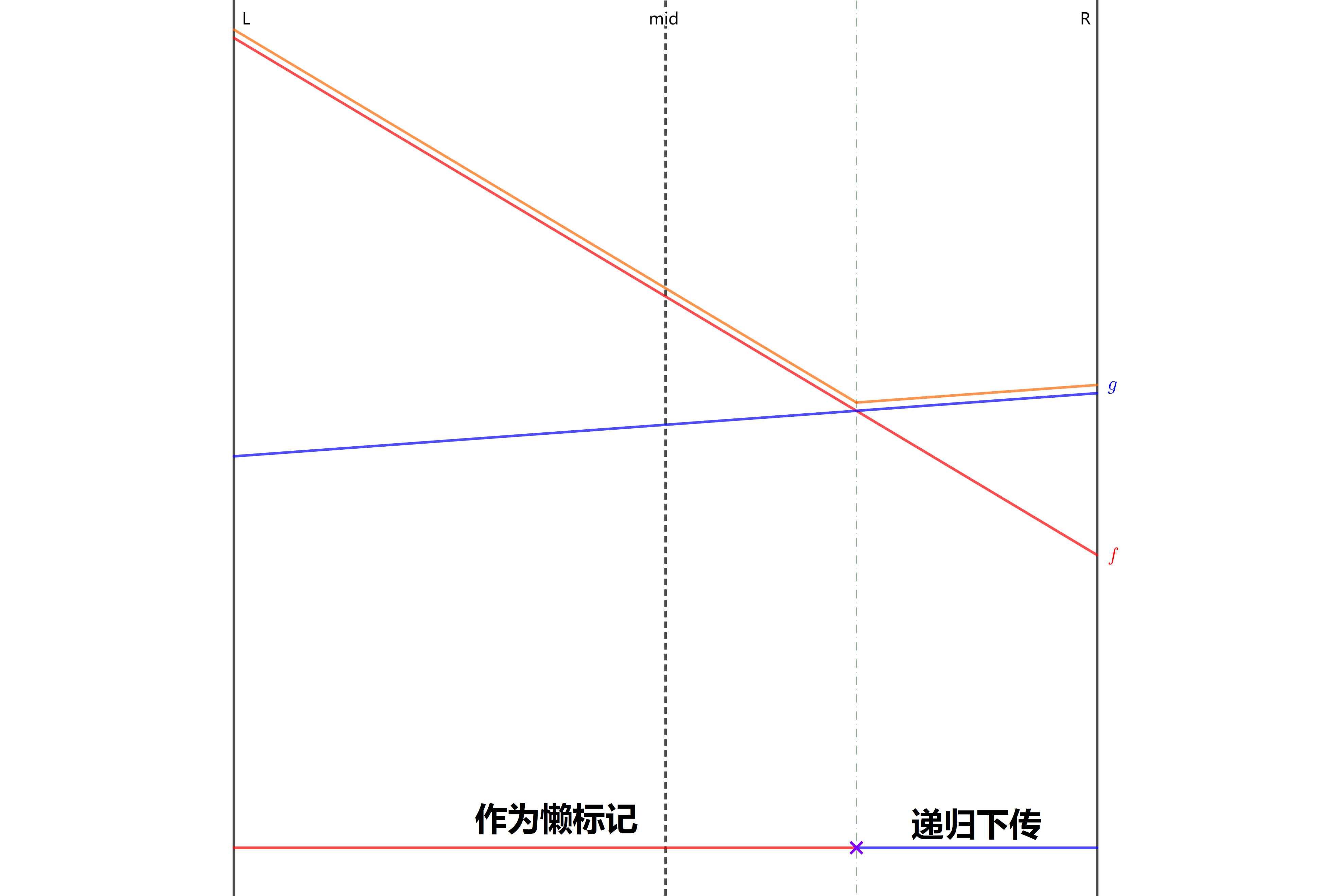
inline ld calc(int id,int x) { return l[id].k*x+l[id].b; } // 计算第 id 条线段上 x 坐标对应的 y 坐标
inline int cmp(ld x,ld y) { return (x>y?1:-1)*(fabs(x-y)>eps); } // 比较高度，前高为 1， 后高为 -1，相等为 0
void cover(int x,int l,int r,int id) {
	int &now=bst[x],mid=l+r>>1;
	if(cmp(calc(id,mid),calc(now,mid))==1) std::swap(id,now); // 判定当前区间最优线段
	int ljud=cmp(calc(id,l),calc(now,l)),rjud=cmp(calc(id,r),calc(now,r));
	if(ljud==1||(!ljud&&id<now)) cover(ls,l,mid,id);
	if(rjud==1||(!rjud&&id<now)) cover(rs,mid+1,r,id); // 递归判断子节点
}

由于区间对应的最优线段不一定是区间内任意一点的最优线段，所以我们采用 标记永久化 的思想，找到当前点对应的最优线段。

pdi max(pdi x,pdi y) { int jud=cmp(x.first,y.first); return ~jud?jud-1?x.second<y.second?x:y:x:y; } // 返回高的那一条线段，同高则返回最小的
pdi query(int x,int l,int r,int pos) {
	if(r<pos||pos<l) return {0,0};
	int mid=l+r>>1;
	ld h=calc(bst[x],pos);
	if(l==r) return {h,bst[x]};
	return max({h,bst[x]},max(query(ls,l,mid,pos),query(rs,mid+1,r,pos)));
}

至此全部内容结束。放上例题的 $AC Code$ ：

#include<bits/stdc++.h>
#define ll long long
#define ld long double
#define ls x<<1
#define rs x<<1|1
#define pdi std::pair<ld,int>
#define fsp(x) std::fixed<<std::setprecision(x)
#define forE(u) for(int p=head[u],v=E[p].to;p;p=E[p].next,v=E[p].to)
const int N=1e5+5,mod=39989;
const ld eps=1e-9;
int n,lastans=0,cnt,bst[N<<4];
inline void decx(int &x) { x=(x+lastans-1+mod)%mod+1; }
inline void decy(int &y) { y=(y+lastans-1+1000000000)%1000000000+1; }
struct line { ld k,b; } l[N];
void analyze(int ax,int ay,int bx,int by) {
	++cnt;
	if(ax==bx) l[cnt].k=0,l[cnt].b=std::max(ay,by);
	else l[cnt].k=(ld)(by-ay)/(bx-ax),l[cnt].b=ay-l[cnt].k*ax;
}
inline ld calc(int id,int x) { return l[id].k*x+l[id].b; }
inline int cmp(ld x,ld y) { return (x>y?1:-1)*(fabs(x-y)>eps); }
void cover(int x,int l,int r,int id) {
	int &now=bst[x],mid=l+r>>1;
	if(cmp(calc(id,mid),calc(now,mid))==1) std::swap(id,now);
	int ljud=cmp(calc(id,l),calc(now,l)),rjud=cmp(calc(id,r),calc(now,r));
	if(ljud==1||(!ljud&&id<now)) cover(ls,l,mid,id);
	if(rjud==1||(!rjud&&id<now)) cover(rs,mid+1,r,id);
}
void modify(int x,int L,int R,int l,int r,int id) {
	if(l<=L&&R<=r) return cover(x,L,R,id);
	int M=L+R>>1;
	if(l<=M) modify(ls,L,M,l,r,id);
	if(M<r) modify(rs,M+1,R,l,r,id);
}
pdi max(pdi x,pdi y) { int jud=cmp(x.first,y.first); return ~jud?jud-1?x.second<y.second?x:y:x:y; }
pdi query(int x,int l,int r,int pos) {
	if(r<pos||pos<l) return {0,0};
	int mid=l+r>>1;
	ld h=calc(bst[x],pos);
	if(l==r) return {h,bst[x]};
	return max({h,bst[x]},max(query(ls,l,mid,pos),query(rs,mid+1,r,pos)));
}
int main() {
	std::ios::sync_with_stdio(false);
	std::cin.tie(nullptr); std::cout.tie(nullptr);
	std::cin>>n;
	for(int i=1,opt;i<=n;++i) {
		std::cin>>opt;
		if(opt) {
			int ax,ay,bx,by; 
			std::cin>>ax>>ay>>bx>>by;
			decx(ax),decx(bx),decy(ay),decy(by);
			if(ax>bx) std::swap(ax,bx),std::swap(ay,by);
			analyze(ax,ay,bx,by);
			modify(1,1,mod,ax,bx,cnt);
		}
		else {
			int x; std::cin>>x; decx(x);
			std::cout<<(lastans=query(1,1,mod,x).second)<<'\n';
		}
	}
}

复杂度分析：每次插入线段要先在 modify 找到值域覆盖区间，再用 cover 选择区间最优线段，每一个操作贡献一个 $\log$ ，查询时标记永久化导致其始终是 $\log$ ，故总复杂度 $O (m \log^{2} n + q \log n)$ 。

7.19 - 基础分块与离线算法

1. 基本分块

经典问题：区间加法，区间求和。分块大小 $\sqrt{n}$ ，复杂度 $O (m \sqrt{n})$ 。
分块 $=$ 多叉线段树：一般的， $n^{1 / 2}$ 叉线段树。这个说法不完全正确，但是可以方便理解。这意味着 pushup 和 pushdown 都可照常进行，且可以利用 标记永久化 的思想保证单点求值的复杂度。

如果是在 $K$ 叉线段树上解决经典问题，复杂度将是 $O (K \log_{K} n)$ 。而当 $K = 2$ 时，就是最经典的线段树了。
分块 $=$ 设定阈值：这才是最正统的理解方式，设定一个阈值 $B$ ，将问题拆解成 零散块（使用暴力） 和 整块（批量处理） 两部分，并期待两部分复杂度达到平衡。
简单题经验：分块并不一定真的要分，他最重要的是思想，把 设定阈值 的概念推广到很多的问题，使其两部分复杂度达到平衡。

笔者注：这里的“简单题”是对于 zjr 来说，对于笔者来说显然很难，基本都是 CF Rating 3000+。
可持久化分块：本质是 可持久化多叉线段树，空间 $O (n^{1 + ϵ})$ ，修改复杂度 $O (n^{ϵ})$ ，查询复杂度 $O (1)$ 或 $O (n^{ϵ})$ 。（其实不是很实用）

2. 莫队

经典问题：区间不同个数。
普通莫队：zjr 是真啥也不说啊，我 bdfs 口胡一下吧先。

我们先考虑一些 不满足低复杂度区间可加性 的问题，这意味着这个东西没法用普通线段树、分块、BIT 来维护，比如 区间内不同数字个数。这意味着我们最先想到的是对其暴力。

这里的低复杂度区间可加性，形如线段树的 pushup 或分块的两个块答案合并，他们可以在 $O (1)$ 的时间内合并区间答案，这就很 nice。显然，如果你想区间维护不同个数，那么在相加的时候你要把两段区间的出现次数记录数组 $c n t$ 加在一起，这太大了，对吧。

但是我们注意到，我们可以在 $O (1)$ 复杂度内将区间答案 扩展或缩小，即从 $[l, r]$ 扩展到 $[l - 1. r], [l + 1, r], [l, r - 1], [l, r + 1]$ 。所以，在可以离线的情况下，我们就可以采取一些小手法，把暴力的复杂度降亿点点。

原始想法你肯定能想出来，考虑按照 $l, r$ 的第一、二关键字排序，这样下一个查询区间就可以借上一个区间的“东风”，用较少的端点移动解决问题。想一想，这可以卡吗？

可以啊， $[1, 1], [1, 10^{6}], [2, 2], [2, 10^{6}], \dots$ 这不是分分钟的事？所以为了防止这个 B 指针反复乱跳，我们考虑用分块压一压。即先对其分块，然后按照 $b e l o n g_{l}, b e l o n g_{r}$ 作为第一、二关键字排序，这样复杂度就得到了基本的保证。

左端点移动次数 $O (m B + n)$ ，右端点 $O (n^{2} / B)$ ，总移动次数 $O (n \sqrt{m})$ 。时间复杂度 $O (m \sqrt{n})$ 。
一个优化：奇偶性排序， $b e l o n g_{l}$ 是奇数则第二关键字 $b e l o n g_{r}$ 顺序，否则倒序。这样可以让一个奇块的处理之后对下一个块（偶块）处理的时候右端点移动的距离更小，从而再压一下时间。
带修莫队：再加一维时间，按照 $b e l o n g_{l}, b e l o n g_{r}, t i m e$ 三个关键字排列即可。

如果你带修，那么意味着你能在 $O (1)$ 内把时间向前 / 后推动一个单位。
多维莫队：升一维，四指针，启动！
不删除莫队 / 回滚莫队：当你不会删除但会添加，here comes the 回滚莫队。
只删除莫队：上面那个完全反过来。
树上莫队：两种方法：
1. 树上分块：好像好多人都不会，下一个。
2. 欧拉序：不错，就用这个。
莫队二次离线：比如区间求逆序对，用莫队维护一个 BIT，把 BIT 的修改和查询也离线下来，所以叫二次离线，以 $O (n \sqrt{n} + n \log n)$ 的复杂度终结全场。

3. 四毛子

made，他又当我会了，先鸽了，有空再补。

7.20 - 平衡树与 LCT

1. 普通平衡树

1.1 起源：BST

期望复杂度： $O (\log n)$
可以被卡成链

1.2 平衡树

使其（均摊）复杂度达到 $O (\log n)$
FHQ - Treap：Treap $=$ Tree $+$ heap. 构建一个 Treap，随机键值，以分裂和合并为基础操作。
Splay：以 rotate 实现的 splay 为基础操作，万物旋到根。

2. LCT

采用 Splay 维护，减下使用其他平衡树维护时的一个 $\log$ ，均摊复杂度 $Θ (m \log n)$
用于维护森林，本质是对每棵树进行实链剖分。

什么是实链？

实链是可以是任意链。你可以在一个点的所有出边中为其钦定一个实边，由实边连成的链就是实链。在 LCT 中，事实上每一棵 Splay 都是在维护一条实链。实链是可变的，你可以灵活地决定哪个边是实边。
实链之间用虚边连接，牢记口诀 认父不认子。

为何认父不认子？

一棵 Splay 上每个节点最多有两个儿子。为了继续使用 Splay 的性质，我们不能改变这个设定，但一颗 Splay 的根结点本来是没有父亲的，我们可以通过给根节点设定父亲的方法连接虚边，将两棵 Splay 连接起来。
以 access 为核心传承 Splay 万物旋到根大法。

7.21 - 可持久化 DS 以及重剖、树上启发式合并、点分治

1. 可持久化数据结构

1.1 主席树

即 可持久化值域线段树，经典问题是 区间第 k 大。

树上路径第 $k$ 小：每个节点一个主席树，在 $x, y, lca (x, y), f a (lca (x, y))$ 上线段树二分即可。（路径上的序列为 ${a_{x}} + {a_{y}} - {a_{lca (x, y)}}$ ）
带修第 $k$ 小：BIT 上套值域线段树即可。

1.2 可持久化区间加

标记永久化

1.3 可持久化并查集

按秩合并，维护可持久化数组存每个点父亲， $O (m \log^{2} n)$

2. 树上启发式合并

即 dsu on tree。

什么是“启发式”？

启发式算法是基于人类的经验和直观感觉，对一些算法的优化。比如并查集的 按秩合并，人类智慧让我们知道显然应该是小子树并入大子树更优。这就是启发式。

树上如何启发式呢？

我们自然应该根据我们的经验，思考一下，当我们需要统计每一个子树信息的时候，按怎样的顺序才能让我们删除无用信息的次数更少。换言之，哪里继承的信息是最多的。

相信你应该能领悟到，这就是重链。

3. 树分治

3.1 点分治

树的重心： $\exists 一或两个 u, s.t.$

$当 u 为树根时， \forall v is a son of u, s i z e_{v} \leq \frac{s i z e_{u}}{o u t d e g r e e_{u}} .$
选取树的重心，删掉并分治其子树。

7.22 - 长链剖分、虚树与线段树进阶

1. 长链剖分

类似于重链剖分，把重链换成长链。

长链：我们定义连接子树深度最深的儿子为长边，长边连成一条长链。

长链剖分的用处不多，一个经典用途是 求解树上 $k$ 级祖先。

要解决这一问题，单纯使用倍增存在 $O (n \log n)$ 预处理， $O (\log n)$ 查询的方法，但事实上还能更快。

我们考虑如何借助长链剖分解决这一问题。我们找到最大的 $2^{i} \leq k$ ，通过倍增跳到其 $2^{i}$ 级祖先。此时，根据长链的定义，这条链长度必然 $\geq 2^{i}$ ，因为长链是最长的，而你是从这么深的地方跳过来的；又必然有 $k - 2^{i} < 2^{i}$ ，所以如果有方法快速查询这条链上的祖先，我们就可以做到 $O (1)$ 的查询——一次跳倍增，一次查链。

这显然是可以做到的，我们需要做的只是，对于每条长链，如果链长度为 $l$ ，存储一下长链底部的前 $2 l - 1$ 级祖先即可，换言之，就是记录下这条长链和长链的根的前 $l - 1$ 级祖先。

最后统计下来就是，长链剖分 $O (n)$ ，倍增预处理祖先 $O (n \log n)$ ，预处理每条链 $2 l - 1$ 级祖先 $O (n)$ ，预处理对数 $O (n)$ ，故复杂度为预处理 $O (n \log n)$ ，查询 $O (1)$ 。

下面是 P5903 【模板】树上 k 级祖先的代码：

// Author: MichaelWong
// Code: C++14(GCC 9)
// Date: 2023/8/24
// File: 【模板】树上 k 级祖先.cpp
#include<bits/stdc++.h>
#define ll long long
#define ld long double
#define pii std::pair<int,int>
#define fsp(x) std::fixed<<std::setprecision(x)
#define forE(u) for(int p=head[u],v=to[p];p;p=next[p],v=to[p])

#define ui unsigned int
ui s;
inline ui get(ui x) {
	x ^= x << 13;
	x ^= x >> 17;
	x ^= x << 5;
	return s = x; 
}

const int N=5e5+5;
ll ans;
int n,q,root,dep[N],d[N],anc[N][20],lg[N],son[N],top[N],lastans;
int cnt,head[N],to[N],next[N];
std::vector<int> up[N],dn[N];
inline void add(int u,int v) { to[++cnt]=v,next[cnt]=head[u],head[u]=cnt; }
inline void acquire(int &x,int &k) { x=(get(s)^lastans)%n+1,k=(get(s)^lastans)%d[x]; }
void dfs(int u) {
	dep[u]=d[u]=d[anc[u][0]]+1;
	for(int i=1;i<=lg[dep[u]];++i) anc[u][i]=anc[anc[u][i-1]][i-1];
	forE(u) dfs(v),dep[v]>dep[u]&&(dep[u]=dep[v],son[u]=v);
}
void NB_dfs(int u,int tp) {
	top[u]=tp;
	if(u==tp) {
		for(int i=0,v=u;i<=dep[u]-d[u];++i) up[u].push_back(v),v=anc[v][0];
		for(int i=0,v=u;i<=dep[u]-d[u];++i) dn[u].push_back(v),v=son[v];
	}
	son[u]&&(NB_dfs(son[u],tp),0);
	forE(u) v^son[u]&&(NB_dfs(v,v),0);
}
inline int query(int x,int k) {
	if(!k) return x;
	x=anc[x][lg[k]],k-=1<<lg[k],k-=d[x]-d[top[x]],x=top[x];
	return k>=0?up[x][k]:dn[x][-k];
}
int main() {
	std::ios::sync_with_stdio(false);
	std::cin.tie(nullptr); std::cout.tie(nullptr);
	std::cin>>n>>q>>s; lg[0]=-1;
	for(int i=1;i<=n;++i) std::cin>>anc[i][0],add(anc[i][0],i),!anc[i][0]&&(root=i),lg[i]=lg[i>>1]+1;
	dfs(root),NB_dfs(root,root);
	for(int i=1,x,k;i<=q;++i) acquire(x,k),ans^=1ll*i*(lastans=query(x,k));
	std::cout<<ans<<'\n';
	return 0;
}
// The code was submitted on Luogu.
// Version: 1.
// If I filled in nothing on the statement,
// it means I'm in a contest and I have no time to do this job.

2. 虚树

3. 线段树分治

吹的高大上，实际上本质是 线段树遍历。

考虑这样一个问题：

有一些操作，每个操作只在 $l \sim r$ 的时间段内有效。

有一些询问，每个询问某一个时间点所有操作的贡献。

对于这样的询问，我们可以离线后 在时间轴上建一棵线段树，这样对于每个操作，相当于在线段树上进行区间操作。

遍历整颗线段树，到达每个节点时执行相应的操作，然后继续向下递归，到达叶子节点时统计贡献，回溯时撤销操作即可。

这样的思想被称为线段树分治，可以在低时间复杂度内解决一类 在线算法并不优秀 的问题。

——xht，《题解 P5787 【二分图 /【模板】线段树分治】》

线段树分治的优点是，不需要每个时间点都从最初开始修改到当前时间点状态，可以借助线段树将复杂度降到线性对数级别。当然，前提是你得有一个 可撤销 的数据结构来支持你回溯。比如模板题中，我们用到了 可撤销并查集。

模板题的代码：

// Author: MichaelWong
// Code: C++14(GCC 9)
// Date: 2023/8/25
// File: 【模板】线段树分治.cpp
#include<bits/stdc++.h>
#define ll long long
#define ld long double
#define ls x<<1
#define rs x<<1|1
#define pii std::pair<int,int>
#define fsp(x) std::fixed<<std::setprecision(x)
#define forE(u) for(int p=head[u],v=to[p];p;p=next[p],v=to[p])
const int N=1e5+5;
int n,m,k,from[N<<1],to[N<<1];
std::vector<int> E[N<<2];
namespace DSU {
	int fa[N<<1],size[N<<1],top=0;
	struct data { int x,y,xfa,yfa; } s[N<<1];
	inline void init() { for(int i=1;i<=n<<1;++i) fa[i]=i,size[i]=1; }
	int get(int x) { return fa[x]==x?x:get(fa[x]); }
	inline void merge(int x,int y) {
		int xfa=get(x),yfa=get(y);
		if(xfa==yfa) return;
		if(size[xfa]<size[yfa]) std::swap(xfa,yfa);
		fa[yfa]=xfa,size[xfa]+=size[yfa],s[++top]={x,y,xfa,yfa};
	}
	inline void undo() { fa[s[top].yfa]=s[top].yfa,size[s[top].xfa]-=size[s[top].yfa],--top; }
}
using namespace DSU;
void modify(int x,int L,int R,int l,int r,int id) {
	if(l<=L&&R<=r) return E[x].push_back(id);
	if(R<l||r<L) return;
	int M=L+R>>1;
	modify(ls,L,M,l,r,id),modify(rs,M+1,R,l,r,id);
}
void solve(int x,int l,int r) {
	int pos=top,flag=1;
	for(int i:E[x]) {
		if(get(from[i])==get(to[i])) { for(int i=l;i<=r;++i) std::cout<<"No\n"; flag=0; break; }
		merge(from[i],to[i]+n),merge(from[i]+n,to[i]);
	}
	if(flag) {
		if(l==r) std::cout<<"Yes\n";
		else {
			int mid=l+r>>1;
			solve(ls,l,mid),solve(rs,mid+1,r);
		}
	}
	while(top!=pos) undo();
}
int main() {
	std::ios::sync_with_stdio(false);
	std::cin.tie(nullptr); std::cout.tie(nullptr);
	std::cin>>n>>m>>k;
	for(int i=1,l,r;i<=m;++i) std::cin>>from[i]>>to[i]>>l>>r,modify(1,1,k,l+1,r,i);
	init(),solve(1,1,k);
	return 0;
}
// The code was submitted on Luogu.
// Version: 1.
// If I filled in nothing on the statement,
// it means I'm in a contest and I have no time to do this job.

4. 线段树进阶

历史最大值
区间取 min
标记永久化
Ex：吉老师线段树
线段树合并卡空间
树剖进阶

4.1 历史区间最值问题：吉老师线段树

一个经典的例子是 P4314 CPU 监控，他是在经典的区间最值、区间加、区间覆盖的线段数上添加了 区间历史最大值 操作。这可以通过标记处理。

不能直接通过维护历史最大值解决，是因为儿子节点的更新会因不及时产生错误，所以必须同时记录 历史最大加值与历史最大覆盖值。

关于 标记就是操作序列 的思想和这道题的 hack 与具体做法，建议阅读核仁的题解和 Froggy 的题解。

// Author: MichaelWong
// Code: C++14(GCC 9)
// Date: 2023/8/25
// File: CPU 监控.cpp
#include<bits/stdc++.h>
#define ll long long
#define ld long double
#define ls x<<1
#define rs x<<1|1
#define pii std::pair<int,int>
#define fsp(x) std::fixed<<std::setprecision(x)
#define forE(u) for(int p=head[u],v=to[p];p;p=next[p],v=to[p])
const int N=1e5+5,inf=INT_MAX;
inline void read(int &x) {
	char ch=getchar(); int sign=1; x=0;
	while(!isdigit(ch)) ch=='-'&&(sign*=-1),ch=getchar();
	while(isdigit(ch)) x=(x<<3)+(x<<1)+(ch^48),ch=getchar();
	x*=sign;
}
inline void read(char &c) {
	c=getchar();
	while(!isalpha(c)) c=getchar();
}
void write(int x,const signed char &tail=-1) {
	x<0&&(putchar('-'),x*=-1);
	x>=10&&(write(x/10),0);
	putchar(x%10+'0');
	~tail&&(putchar(tail),0);
}
int n,m,val[N],pls[N<<2],hpl[N<<2],iscov[N<<2],cvr[N<<2],hcv[N<<2],max[N<<2],hmx[N<<2];
inline void ptcover(int x,int num,int hnum) {
	if(iscov[x]) hcv[x]=std::max(hcv[x],hnum);
	else iscov[x]=1,hcv[x]=hnum;
	hmx[x]=std::max(hmx[x],hnum);
	cvr[x]=max[x]=num,pls[x]=0;
}
inline void ptplus(int x,int num,int hnum) {
	hpl[x]=std::max(hpl[x],pls[x]+hnum);
	hmx[x]=std::max(hmx[x],max[x]+hnum);
	pls[x]+=num,max[x]+=num;
}
inline void ptmodify(int x,int num,int hnum) { iscov[x]?ptcover(x,cvr[x]+num,cvr[x]+hnum):ptplus(x,num,hnum); }
inline void pushup(int x) { max[x]=std::max(max[ls],max[rs]),hmx[x]=std::max(hmx[x],max[x]); }
inline void pushdown(int x) {
	ptmodify(ls,pls[x],hpl[x]),ptmodify(rs,pls[x],hpl[x]);
	pls[x]=hpl[x]=0;
	if(!iscov[x]) return;
	ptcover(ls,cvr[x],hcv[x]),ptcover(rs,cvr[x],hcv[x]);
	iscov[x]=cvr[x]=hcv[x]=0;
}
void build(int x,int l,int r) {
	if(l==r) return hmx[x]=max[x]=val[l],void();
	int mid=l+r>>1;
	build(ls,l,mid),build(rs,mid+1,r),pushup(x);
}
void modify(int x,int L,int R,int l,int r,int val) {
	if(l<=L&&R<=r) return ptmodify(x,val,val);
	if(R<l||r<L) return;
	int M=L+R>>1; pushdown(x);
	modify(ls,L,M,l,r,val),modify(rs,M+1,R,l,r,val),pushup(x);
}
void cover(int x,int L,int R,int l,int r,int val) {
	if(l<=L&&R<=r) return ptcover(x,val,val);
	if(R<l||r<L) return;
	int M=L+R>>1; pushdown(x);
	cover(ls,L,M,l,r,val),cover(rs,M+1,R,l,r,val),pushup(x);
}
int query(int x,int L,int R,int l,int r) {
	if(l<=L&&R<=r) return max[x];
	if(R<l||r<L) return -inf;
	int M=L+R>>1; pushdown(x);
	return std::max(query(ls,L,M,l,r),query(rs,M+1,R,l,r));
}
int hisquery(int x,int L,int R,int l,int r) {
	if(l<=L&&R<=r) return hmx[x];
	if(R<l||r<L) return -inf;
	int M=L+R>>1; pushdown(x);
	return std::max(hisquery(ls,L,M,l,r),hisquery(rs,M+1,R,l,r));
}
int main() {
	read(n);
	for(int i=1;i<=n;++i) read(val[i]);
	build(1,1,n);
	read(m);
	for(int i=1;i<=m;++i) {
		char opt; int x,y,z;
		read(opt),read(x),read(y);
		if(opt=='Q') write(query(1,1,n,x,y),'\n');
		else if(opt=='A') write(hisquery(1,1,n,x,y),'\n');
		else if(opt=='P') read(z),modify(1,1,n,x,y,z);
		else if(opt=='C') read(z),cover(1,1,n,x,y,z);
	}
	return 0;
}
// The code was submitted on Luogu.
// Version: 1.
// If I filled in nothing on the statement,
// it means I'm in a contest and I have no time to do this job.

7.23 模拟赛解题报告

今天是 Week 1 的最后一天了！从刚开始的兴致勃勃到后面的如坐针毡，最后又用一场近乎坐牢的模拟赛结束了惨烈的 Week 1，我真是太开心啦！

好了好了说认真的 qwq，觉得 ZR 真的能给你 push 得挺狠，希望能有所进步吧。接下来总结一下今天的模拟赛。

T1 $100 p t s$

算是“签到题”？需要一点点的思维量，正解复杂度 $O (n + \sum | S |)$ ，我多套了一个 $\log$ qwq（遍历写二分了），好在没卡。

T2 $40 p t s$

投入了大量的时间和精力，本来目标是冲着 100 去的，最后也没搞出正解，想到了施展扫描线和线段树，最后没实现 qwq，还导致耽误了大量时间，断送了 T4 的 20 分，警钟撅烂。

T3 $0$

哈哈！真的很难，后两道题难度是指数上升，但是其实暴力能打一点，我水平有限就没打，感觉有点亏。（当然了时间也确实不够。）

正解考虑树上启发式合并，还有细节我还不会 qwq。

T4 $10 p t s$

其实应该写一个逆序对套什么东西， $n^{2}$ 可以有 40 分，但大量时间都浪费在了 T2 上，导致这道题只写了一个 $n^{4}$ 的暴力，不得不说 ZROI 的评测机是真的牛，让我拿了一个点的分 qwq。

正解真的很离谱！后面两道题都相当困难，和前面完全不是一个档次。正解考虑使用分治，加上一些前缀和思想。

总的来说，算是暴露水平了。但是由于策略和心态问题断送了一些分数，引以为戒，下次（8.5）争取有所进步。

但据说以后没有签到题了……

期待 7.28 的欢乐 ACM 吧。

posted @ 2023-07-17 11:39 二两碘酊阅读(184) 评论(1) 编辑收藏举报

刷新页面返回顶部

登录后才能查看或发表评论，立即登录或者逛逛博客园首页

相关博文：

· 关于数据结构

· 停课后学习笔记

· 【6】线段树学习笔记

· 浅谈树链剖分

· 线段树建造

公告

昵称：二两碘酊
园龄： 2年
粉丝： 13
关注： 7

+加关注

2025年3月

日

一

二

三

四

五

六

Michael Wong - 二两碘酊

从 LaTeX 到 C++，从平面设计与摄影构图到视频剪辑与电影艺术，钟爱各类视听逻辑美学与计算机艺术的热血高中少年