机器学习中的评价指标--02

机器学习中的评价指标--02

回归算法的评价指标就是SSE、MSE，RMSE，MAE、R-Squared。下面一一介绍：

SSE(和方差)

该统计参数计算的是拟合数据和原始数据对应点的误差的平方和，计算公式如下

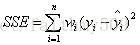
SSE越接近于0，说明模型选择和拟合更好，数据预测也越成功。接下来的MSE和RMSE因为和SSE是同出一宗，所以效果一样。

均方误差（MSE）

MSE （Mean Squared Error）叫做均方误差。看公式

这里的y是测试集上的。

用 真实值-预测值 然后平方之后求和平均。

猛着看一下这个公式是不是觉得眼熟，这不就是线性回归的L2损失函数嘛！！！ 对，在线性回归的时候我们的目的就是让这个损失函数最小。那么模型做出来了，我们把损失函数丢到测试集上去看看损失值不就好了嘛。简单直观暴力！

均方根误差（RMSE）

RMSE（Root Mean Squard Error）均方根误差。

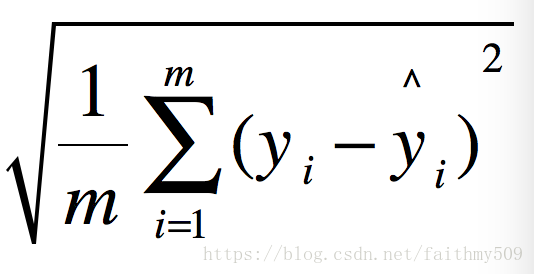
这不就是MSE开个根号么。有意义么？其实实质是一样的。只不过用于数据更好的描述。
例如：要做房价预测，每平方是万元，我们预测结果也是万元。那么差值的平方单位应该是千万级别的。那我们不太好描述自己做的模型效果。于是干脆就开个根号就好了。我们误差的结果就跟我们数据是一个级别的，在描述模型的时候就说，我们模型的误差是多少万元。

MAE

MAE(平均绝对误差)

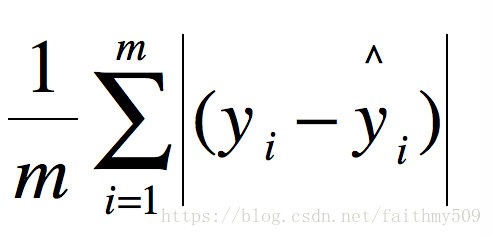
类似L1损失

R Squared

上面的几种衡量标准针对不同的模型会有不同的值。比如说预测房价 那么误差单位就是万元。数值可能是3，4，5之类的。那么预测身高就可能是0.1，0.6之类的。没有什么可读性，到底多少才算好呢？要根据模型的应用场景来。
看看分类算法的衡量标准就是正确率，而正确率又在0～1之间，最高百分之百。最低0。很直观，而且不同模型一样的。那么线性回归有没有这样的衡量标准呢？答案是有的。
那就是R Squared也就是确定系数。

在讲确定系数之前，我们需要介绍另外两个参数SSR和SST，因为确定系数就是由它们两个决定的。

(1)SSR：Sum of squares of the regression，即预测数据与原始数据均值之差的平方和，公式如下

(2)SST：Total sum of squares，即原始数据和均值之差的平方和，公式如下

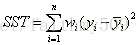
细心的网友会发现，SST=SSE+SSR（我还是算了一下才知道）。而我们的“确定系数”是定义为SSR和SST的比值，故

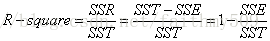
其实“确定系数”是通过数据的变化来表征一个拟合的好坏。由上面的表达式可以知道“确定系数”的正常取值范围为[0 1]，越接近1，表明方程的变量对y的解释能力越强，这个模型对数据拟合的也较好。

代码部分

点击查看代码

只说这个几种衡量标准的原始代码。
MSE
y_preditc=reg.predict(x_test) #reg是训练好的模型
mse_test=np.sum((y_preditc-y_test)**2)/len(y_test) #跟数学公式一样的epredict(x_test) #reg是训练好的模型


RMSE
rmse_test=mse_test ** 0.5_test=mse_test ** 0.5

MAE
mae_test=np.sum(np.absolute(y_preditc-y_test))/len(y_test)


R Squared
1- mean_squared_error(y_test,y_preditc)/ np.var(y_test)

from sklearn.metrics import mean_squared_error #均方误差from sklearn.metrics import mean_absolute_error #平方绝对误差from sklearn.metrics import r2_score#R square#调用

mean_squared_error(y_test,y_predict)

mean_absolute_error(y_test,y_predict)

r2_score(y_test,y_predict).metrics import mean_absolute_error #平方绝对误差from sklearn.metrics import r2_score#R square#调用

mean_squared_error(y_test,y_predict)

mean_absolute_error(y_test,y_predict)

r2_score(y_test,y_predict)