Least Square Solution

Least Square Solution

Please refer to this video for detailed reasoning.

When the equation of \(Ax=b\) establishes, it means that vector \(b\) is within the column space of matrix \(A\) (\(b\in \text{colsp(A)}\)) . But what if we can not find a solution of \(x\) that satisfies the equation? In other words, the vector \(b\) may not be in the column space of matrix \(A\).

What we can do is to find a possible \(x\) that makes \(Ax\) be as close to \(b\) as possible. In other words, we are going to minimize the distance between \(Ax\) and \(b\), which we refer to the minimization of the following formula：

\[\text{min}\{|Ax-b|^2\} \]

As we know, the \(Ax\) indicates the column space of \(A\). To get an intuitive knowledge of that, let's consider this space as a two-dimensional plane and of course, vector \(b\) is not within this plane. And there is a angle between \(b\) and the plane which looks like the vector \(b\) pierces though the plane. So the subtraction of vector \(Ax\) and vector \(b\) is another vector, and in order to get the minimum of its square, it should be prependicular to the plane according to our junior school knowledge. And also \(Ax\) should the corresponding perpendicular projection of \(b\) to the plane.

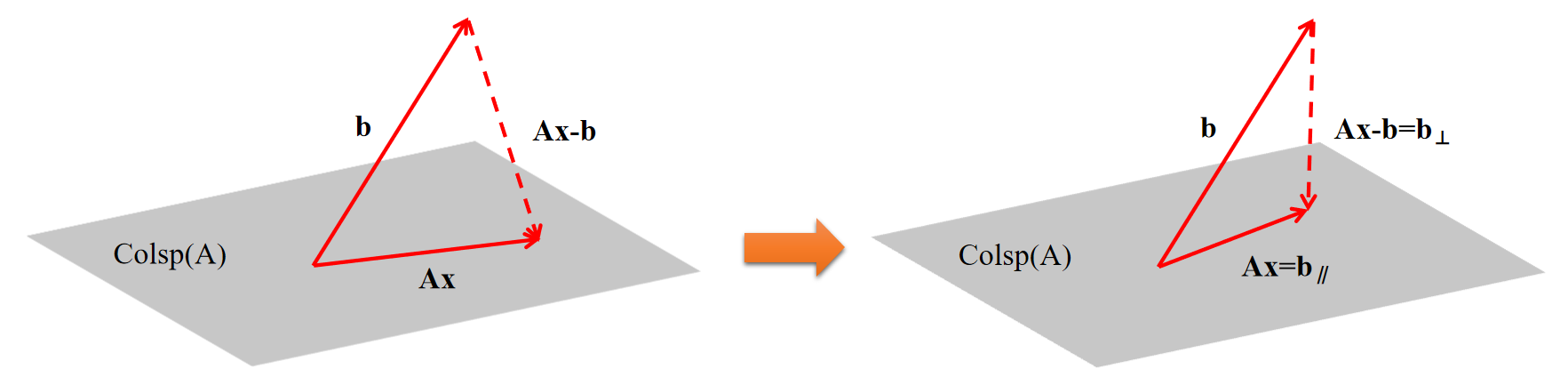
Some the problem becomes solving the following equation:

\[Ax=b_{\parallel}=b-b_{\perp} \]

Then:

\[A^TAx=A^Tb-A^Tb_{\perp} \]

Notice that:

\[A^Tb_{\perp}=\begin{bmatrix}a_1&\cdots&a_n\end{bmatrix}^Tb_{\perp}=\begin{bmatrix}a_1^T\\\vdots\\a_n^T\end{bmatrix}b_{\perp}=\begin{bmatrix}\langle a_1|b_{\perp}\rangle\\\vdots\\\langle a_n|b_{\perp}\rangle\end{bmatrix}=0 \]

Finally we can obtain the least square solution by solving the following equation:

\[A^TAx=A^Tb \]