QR decomposition

QR decompostion

[Wiki](QR decomposition - Wikipedia): QR decomposition is a composition of a matrix A into the product of an orthogonal matrix Q and an upper triangular matrix R.

Let's firtst begin with an example (refer to [Video](QR decomposition - YouTube))

Suppose we have an matrix \(A\) which is represented by:

\[A=\begin{bmatrix}2&3\\2&4\\1&1\end{bmatrix}=\begin{bmatrix}v_1&v_2\end{bmatrix}\\ \text{Here: } v_1=\begin{bmatrix}2\\2\\1\end{bmatrix},v_2=\begin{bmatrix}3\\4\\1\end{bmatrix} \]

Then we shall apply the Gram-Schmidt Orthogonalization:

\[\text{Let: }u_1=v_1=\begin{bmatrix}2\\2\\1\end{bmatrix}\\ u_2=v_2-\frac{(u_1,v_2)}{(u_1,u_1)}u_1=\begin{bmatrix}3\\4\\1\end{bmatrix}-\frac{15}{9}\begin{bmatrix}2\\2\\1\end{bmatrix}=\begin{bmatrix}-1/3\\2/3\\-2/3\end{bmatrix}\\ w_1=\frac{u_1}{||u_1||}=\begin{bmatrix}2/3\\2/3\\1/3\end{bmatrix},w_2=\frac{u_2}{||u_2||}=\begin{bmatrix}-1/3\\2/3\\-2/3\end{bmatrix} \]

And we assign the orthogonal matrix Q to:

\[Q=\begin{bmatrix}w_1 & w_2\end{bmatrix}=\begin{bmatrix}2/3&-1/3\\2/3&2/3\\1/3&-2/3\end{bmatrix} \]

Therefore, R can be obtained by:

\[A=QR\rightarrow Q^TA=Q^TQR=R\\ R=Q^TA=\begin{bmatrix}2/3& 2/3&1/3\\-1/3&2/3&-2/3\end{bmatrix}\begin{bmatrix}2&3\\2&4\\1&1\end{bmatrix}=\begin{bmatrix}3&5\\0&1\end{bmatrix} \]

Is it a coincidence that R is upper triangular matrix? Let's view the process again by substitute those values with the corresponding vector notation:

\[R=Q^TA=\begin{bmatrix}w_1^T\\w_2^T\end{bmatrix}\begin{bmatrix}u_1&u_2\end{bmatrix}=\begin{bmatrix}w_1^Tu_1&w_1^Tu_2\\w_2^Tu_1&w_2^Tu_2\end{bmatrix} \]

Since the projection part of \(v_2\) onto \(v_1\)（\(u_1\)） is eliminated from \(v_2\) which yields \(u_2\)（normalized to \(w_2\)），therefore \(w_2\) is orthogonal to \(u_1\) and therefore the lower triangular entry \(w_2^Tu_1\) becomes zero.

And we can extend this to general cases. According to orthogonalization procedures, the \(i\)-th orthonormal vector \(w_i\) of the matrix \(A_{m\times n}=\begin{bmatrix}v_1&v_2&\cdots&v_i&\cdots&v_n\end{bmatrix}\) is constructed to be orthogonal to all the \(v_j(j<i)\) vectors. ( In other words, the project parts of \(v_i\) onto all \(v_j\)s is eliminated from \(v_i\) which yiels \(u_i\) (normalized to \(w_i\))). And it does not ensure that \(w_i\) is orthogonal to other \(v_j\)s when \(j>i\).

Therefore, for those entries whose row index \(i\) is smaller than column index \(j\), the values will become zero. That's why we finally obtain an upper triangular matrix R.

Consider the more general case. We can factor a complex \(m\times n\) matrix \(A\), with \(m\geq n\), as the prodcut of an \(m\times m\) unitary matrix \(Q\) and an \(m\times n\) upper triangular matrix \(R\), and \(R_1\) refers to the \(n\times n\) non-zero upper triangular matrix of matrix \(R\), while the remaining \(m-n\) rows are all zeros.

Since matrix \(A\) only has \(n\) columns, when deriving the matrix \(R\), the multiplication of \(i\)-th ( \(n<i\leq m\)) row of \(Q^T\) (refer to \(Q_2^T\), and \(Q_1^T\) refer to those rows with index \(i\leq n\)) with the additional all-zero columns of matrix \(A\) (in order to make the matrix size to be \(m\times m\)) will lead to zero.

\[\begin{bmatrix}Q_1^T\\Q_2^T\end{bmatrix}\begin{bmatrix}A &0\end{bmatrix}_{(m\times m)}=\begin{bmatrix}Q_1^TA&0\\Q_2^TA&0\end{bmatrix}=\begin{bmatrix}R_1&0\\0&0\end{bmatrix} \]

Therefore, we have:

\[Q_1^TA=R_1\\ \Rightarrow A=Q_1R_1 \]

Example1:

Using QR decomposition to get the least square solution of linear equation \(Ax=b\):

\[\begin{bmatrix}2&3\\2&4\\1&1\end{bmatrix}x=Ax=b=\begin{bmatrix}7\\3\\1\end{bmatrix} \]

And the least square solution can be obtain by solving the following equation:

\[A^TAx=A^Tb \]

Then by using the QR decomposition, we can obtain:

\[(QR)^TQRx=(QR)^Tb\\ \Rightarrow R^TQ^TQRx=R^TQ^Tb\\ \Rightarrow R^TRx=R^TQ^Tb\\ \text{In most cases, }R^T \text{ is invertible, which means the rank is equal to the colsp(A)}\\ \text{So we can cancel out } R^T:\\ \Rightarrow Rx=Q^Tb \]

And finally, the equation becomes:

\[\begin{bmatrix}3&5\\0&1\end{bmatrix}\begin{bmatrix}x_1\\x_2\end{bmatrix}=\begin{bmatrix}2/3& 2/3&1/3\\-1/3&2/3&-2/3\end{bmatrix}\begin{bmatrix}7\\3\\1\end{bmatrix}=\begin{bmatrix}7\\-1\end{bmatrix}\\ \]

Some we just need to solve the following linear equations:

\[\begin{cases}3x_1+5x_2=7\\x_2=-1\end{cases} \]

which is easier because owing to the upper triangular matrix R, we already know the value of last variable \(x_n\), and we can do this backward recursively until we get the solution. Pretty cool, right?

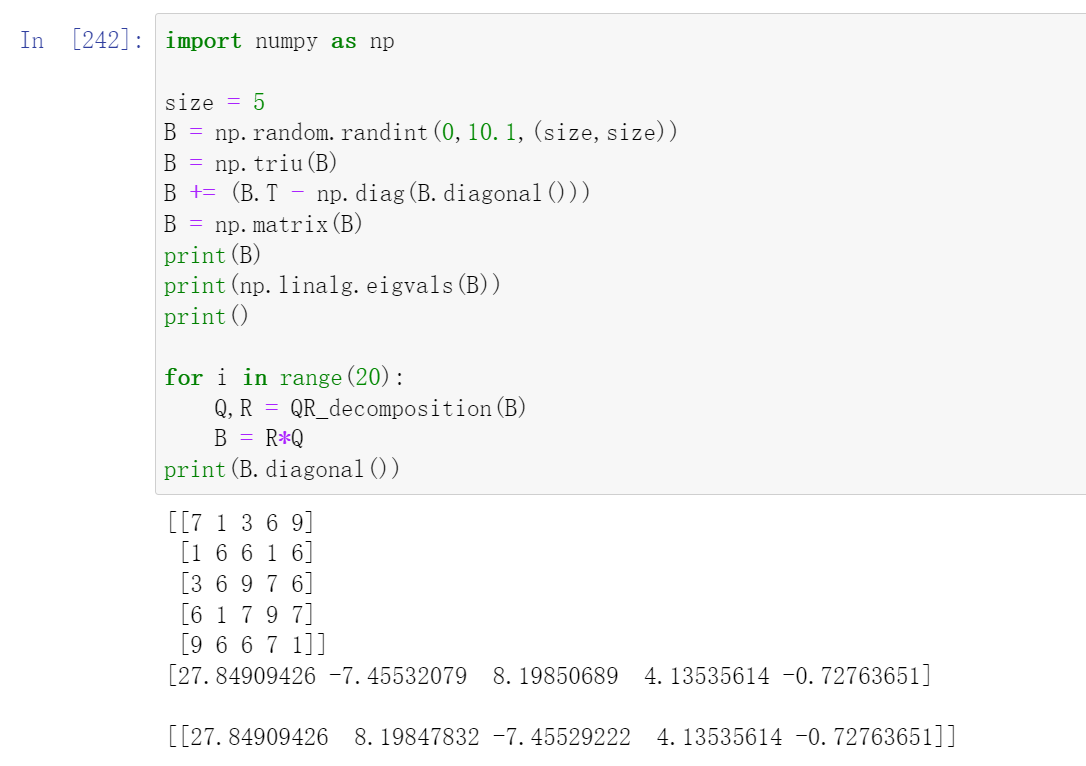
Example2:

Using QR itertation to calculate the eigenvalue and eigenvectors of a matrix. The basic idea is to iteratively performing the QR decomposition.

Under the assumption of QR decomposition, arbitary matrix \(A\) can be decomposed into an orthogonal matrix \(Q\) and an upper triangular matrix \(R\):

\[A=QR \]

Consider another equation:

\[A^{\prime}=RQ \]

If we bring \(R\) into this equation, we obtain:

\[A^{\prime} = Q^TAQ \]

Since \(Q\) is an orthogonal matrix, the above operation is actually an orthogonal(similarity) transformation which results in a similar matrix \(A^{\prime}\) with respect to \(A\). Since similarity transformation will not change the eigenvalues, we can continue to perform this until the values on the diagonal converge to the eigenvalues.