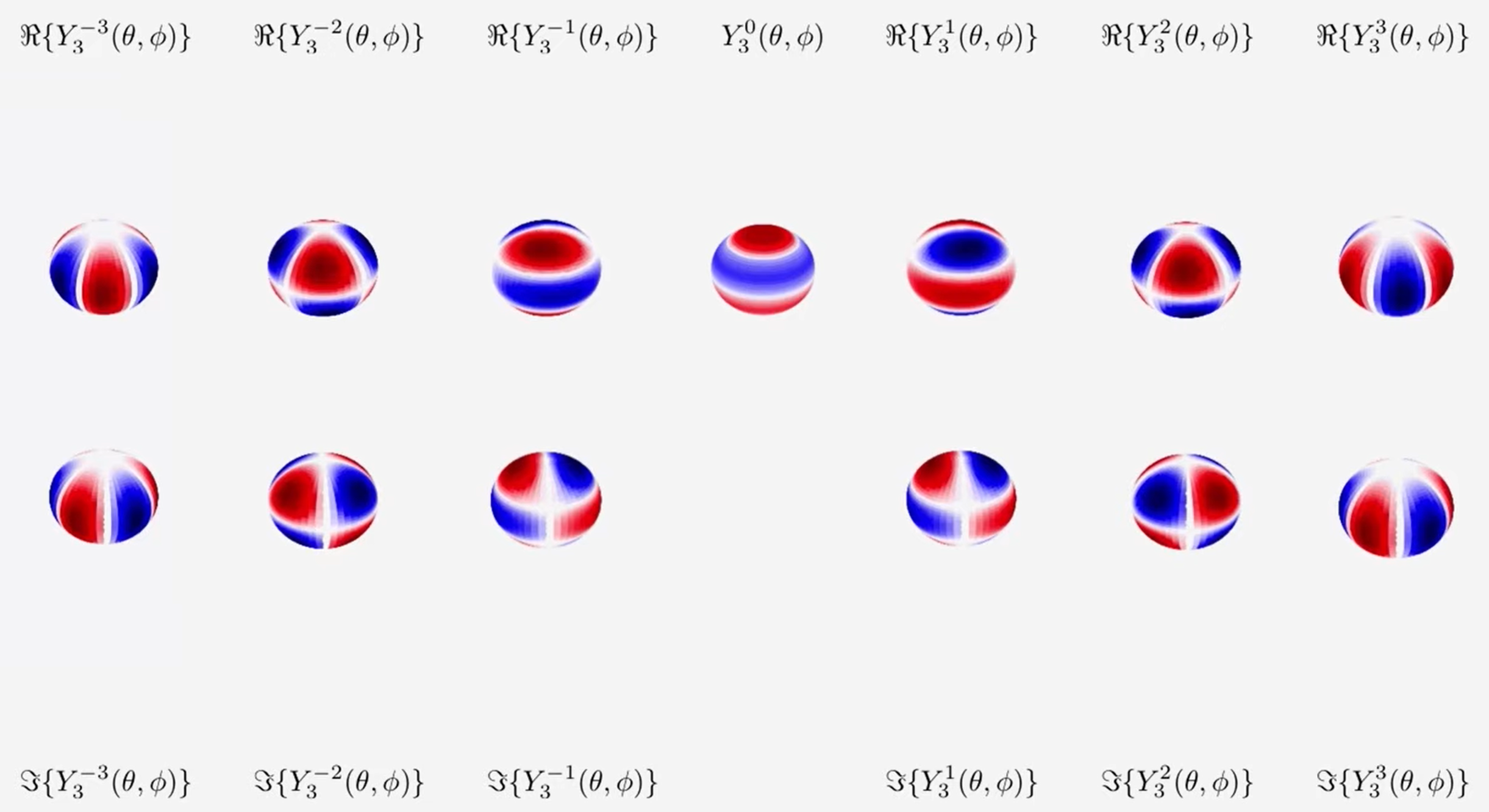
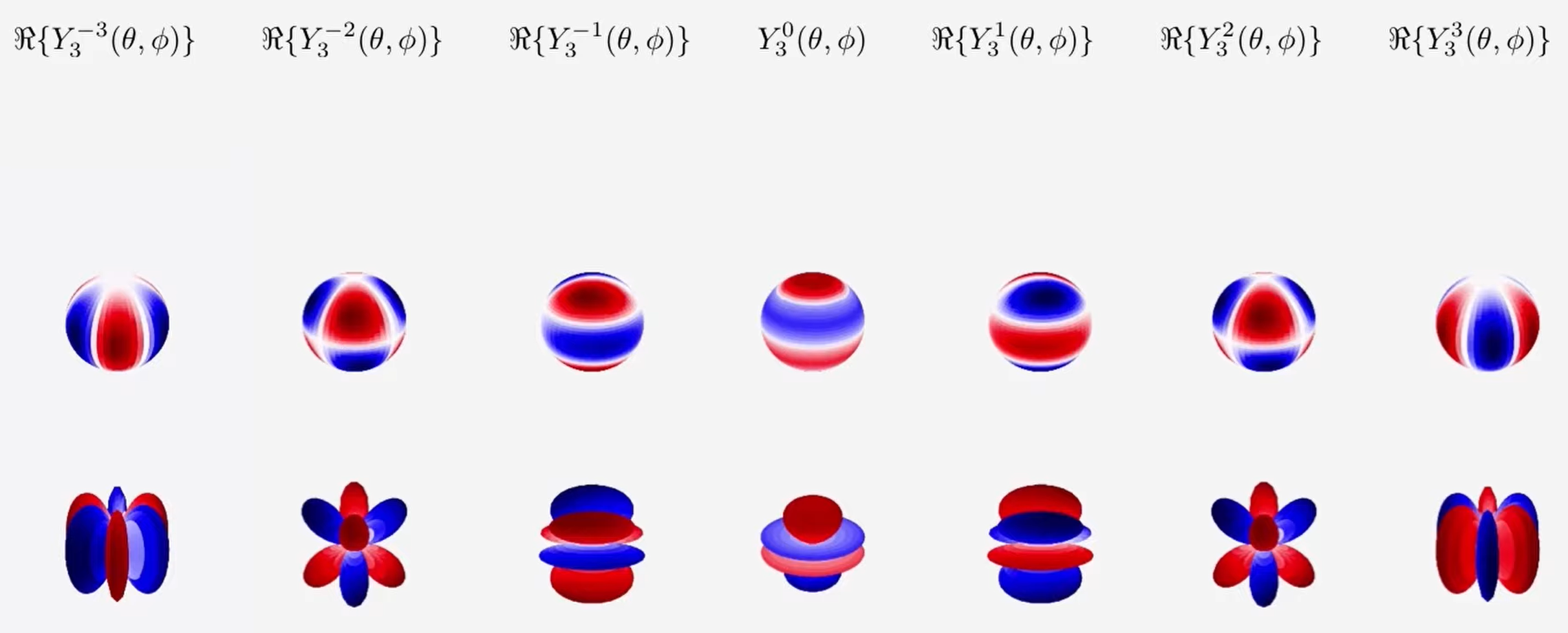
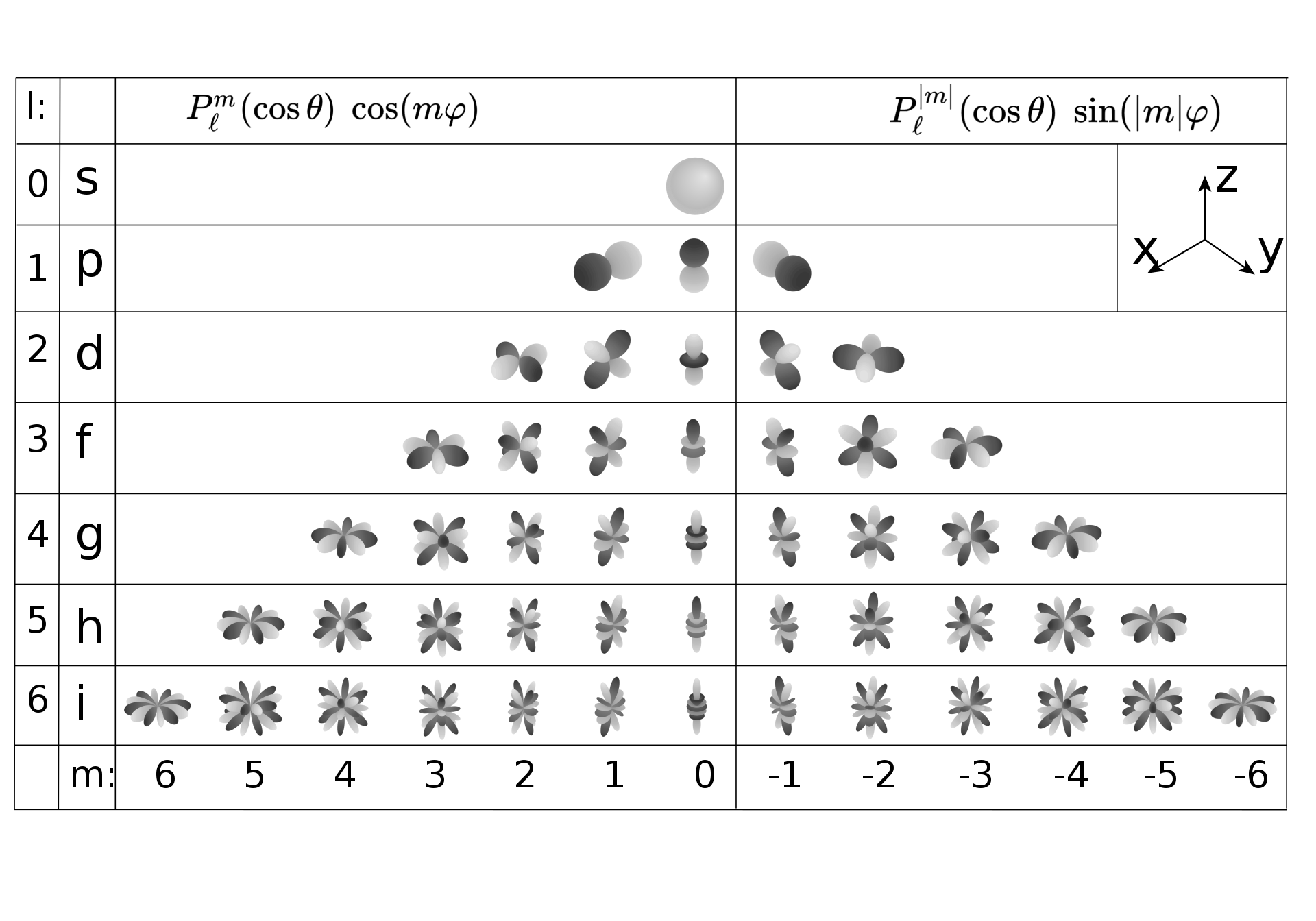
Spherical harmonics
Spherical harmonics
Wiki: Spherical harmonics forms a complete orthogonal functions with each function defined on the sphere.
Spherical harmonics play important roles in Orbital Angular Momentum in quantum mechanis.
We have the following eigen value equations for \(L^2\) and \(L_z\):
\[\hat{L}^2Y_l^m(\theta,\phi)=l(l+1)\hbar^2Y_l^m(\theta,\phi)\\
\hat{L}_zY_l^m(\theta,\phi)=m\hbar Y_l^m(\theta,\phi)\\
\text{Here: }l=0,1,2,\cdots \quad m=-l,-l+1,\cdots,0,\cdots,l-1,l
\]
The sperical harmonics is defined as:
\[Y_l^m(\theta,\phi)=\frac{(-1)^l}{2^ll!}\sqrt{\frac{(2l+1)(l+m)!}{4\pi(l-m)!}}e^{im\phi}(\sin\theta)^{-m}\frac{d^{l-m}}{d^{l-m}(\cos\theta)}(\sin\theta)^{2l}\\
=(-1)^m\sqrt{\frac{(2l+1)(l+m)}{4\pi(l-m)!}}e^{im\phi}P_l^m(\cos\theta)
\]
Here \(P_l^m(\cos\theta)\) is called associated Legendre polynomial.
Consider mutiple values of \((l,m)\):
- \(l=0,m=0\):
\[Y_0^0(\theta,\phi) = \frac{(-1)^0}{2^0\times0!}\sqrt{\frac{(0+1)\times0!}{4\pi\times0!}}e^0(\sin\theta)^0\frac{d^0}{d^0(\cos\theta)}(\sin\theta)^0=\frac{1}{\sqrt{4\pi}}
\]
- \(l=1,m=-1\):
\[Y_1^{-1}(\theta,\phi) = \frac{(-1)^1}{2^1\times1!}\sqrt{\frac{(2+1)\times(1-1)!}{4\pi\times(1+1)!}}e^{-i\phi}(\sin\theta)^1\frac{d^2}{d^2(\cos\theta)}(\sin\theta)^2\\
=-\frac{1}{2}\sqrt{\frac{3}{8\pi}}e^{-i\phi}\sin\theta\frac{d^2}{d^2(\cos\theta)}(1-\cos^2\theta)\\
=-\frac{1}{2}\sqrt{\frac{3}{8\pi}}e^{-i\phi}\sin\theta(-2)\\
=\sqrt{\frac{3}{8\pi}}e^{-i\phi}\sin\theta\\
=\sqrt{\frac{3}{8\pi}}\bigg(\cos\phi-i\sin\phi\bigg)\sin\theta\\
=\sqrt{\frac{3}{8\pi}}\cos\phi\sin\theta-i\sqrt{\frac{3}{8\pi}}\sin\phi\sin\theta
\]
- \(l=1,m=0\):
\[Y_1^0(\theta,\phi)=\sqrt{\frac{3}{4\pi}}\cos\theta
\]
- \(l=1,m=1\):
\[Y_1^1(\theta,\phi)=-\sqrt{\frac{3}{8\pi}}\cos\phi\sin\theta-i\sqrt{\frac{3}{8\pi}}\sin\phi\sin\theta
\]
- \(l=2,m=\pm2\):
\[Y_2^{\pm2}(\theta,\phi)=\sqrt{\frac{15}{32\pi}}e^{\pm2i\phi}\sin^2\theta
\]
- \(l=1,m=\pm1\):
\[Y_2^{\pm1}(\theta,\phi)=-\mp\sqrt{\frac{15}{8\pi}}e^{\pm i\phi}\sin\theta\cos\theta
\]
- \(l=1,m=0\):
\[Y_2^{0}(\theta,\phi)=\sqrt{\frac{5}{16\pi}}(3\cos^2\theta-1)
\]