Gaussian quadrature

Gaussian quadrature

Wiki: Gaussian quadrature indicates that the integral of a function can be replaced as a weight sum of function values at some points.

The Gauss-Legendre quadrature has the integral domain \([-1,1]\) and is stated as:

\[\int_{-1}^1f(x)dx = \sum_{i=1}^nw_if(x_i) \]

Here \(f(x)\) must be a polynomial of degree \(2n-1\) (totally \(2n\) terms) or less, which is approximate by \(2n\) parameters \((w_i,x_i)\).

When the interval is not \([-1,1]\), it should be changed in the following way:

\[\int_a^bf(x)dx=\int_{-1}^1f(\frac{b-a}{2}\xi+\frac{a+b}{2})\frac{dx}{d\xi}d\xi\\ \text{Here: } x=\frac{b-a}{2}\xi+\frac{a+b}{2} \quad \begin{cases}\xi\rightarrow-1,x\rightarrow a\\ \xi \rightarrow 1, x\rightarrow b\end{cases}\\ \therefore dx/d\xi=\frac{b-a}{2}\\ \Rightarrow \int_a^bf(x)dx=\frac{b-a}{2}\sum_{i=1}^n w_if(\frac{b-a}{2}\xi_i+\frac{a+b}{2}) \]

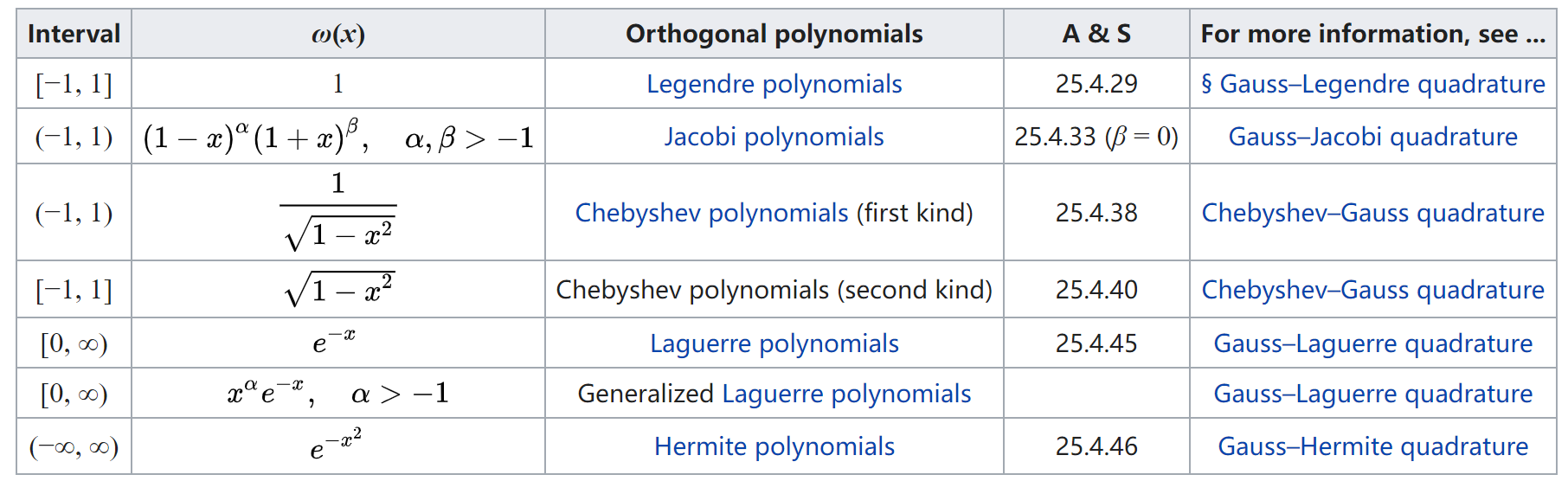
We can choose the corresponding \((w_i, \xi_i)\) pairs in the below table to calculate the integral.

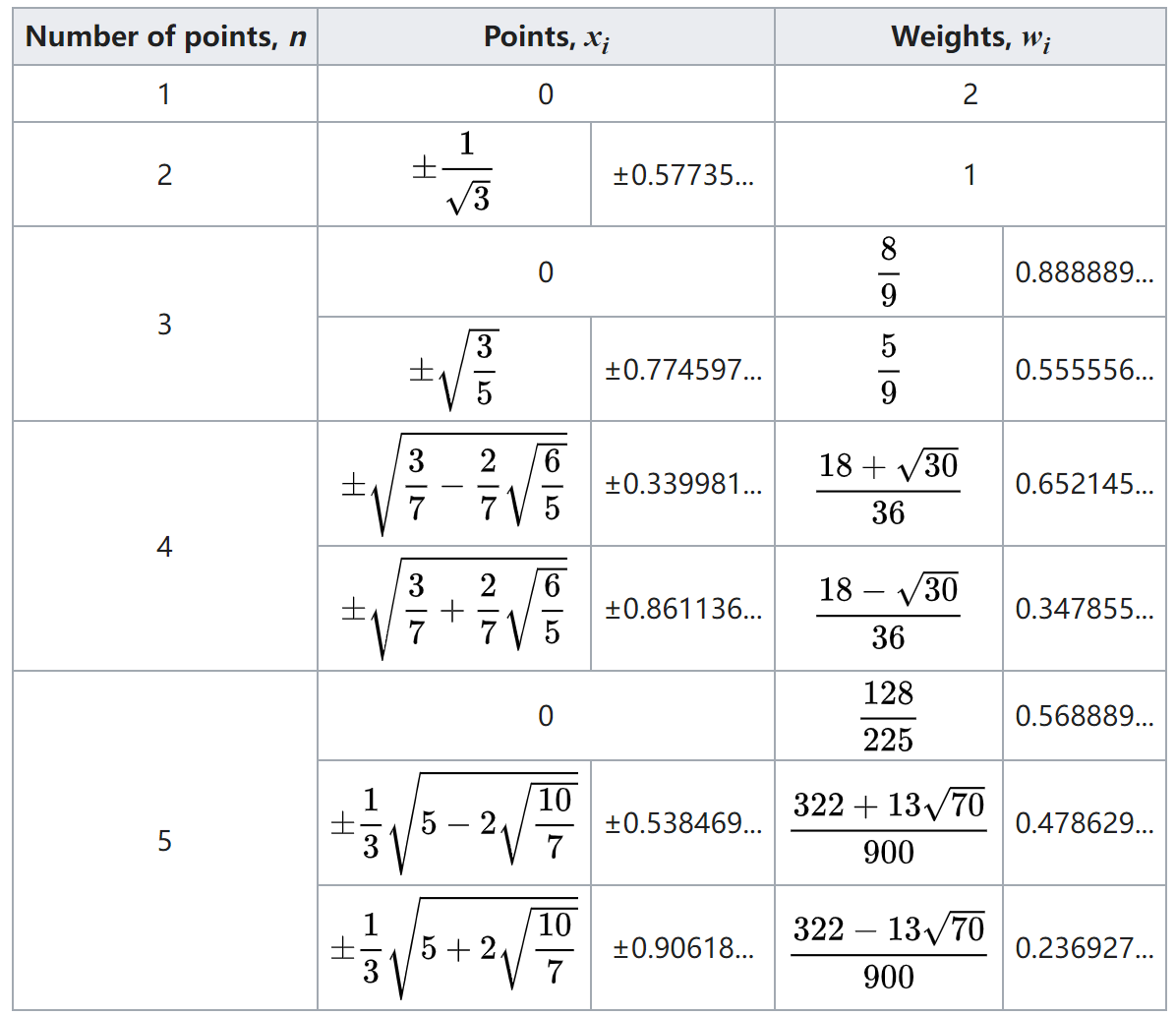
Let's consider a two-point Gauss-Legendre quadrature to determine the \((w_i, x_i)\) pair. Reference Video

Since \(f(x)\) is a part of the Legendre polynomial, suppose in the following case the degree is 3. That means \(f(x)\) is composed of \(1,x,x^2,x^3\). Here the coefficent before each term can be neglacted since it can be cancelled from two sides of the equation:

\[\int_{-1}^1f(x)dx = \sum_{i=1}^nw_if(x_i) \]

Therefore, we have:

\[\int_{-1}^11 dx=2=w_1+w_2 \quad [f(x)=1]\\ \int_{-1}^1xdx=0=w_1x_1+w_2x_2 \quad [f(x)=x]\\ \int_{-1}^1x^2dx=\frac{2}{3}=w_1x_1^2+w_2x_2^2 \quad [f(x)=x^2]\\ \int_{-1}^1x^3x=0=w_1x_1^3+w_2x_2^3 \quad [f(x)=x^3] \]

From the above 4 equations, we can obtain the parameters:

\[w_1=w_2=1,x_1=\frac{1}{\sqrt{3}},x_2=-\frac{1}{\sqrt{3}} \]

There are other forms of Gaussian quadrature with varied choices of intervals and weight functions:

\[\int_a^bw(x)f(x)dx \]