Gram-Schmidt Orthogonalization

Gram-Schmidt Orthogonalization

Wiki: Gram-Schmidt Orthogonalization are utilized to transform a finite number of linear independent vectors belonging to inner product space to a set of orthonormal vectors.

Consider we have a set of linear dependent vectors \(\{v_1,v_2,...,v_n\}\), and the corresponding set of orthogonal vectors is defined as \(\{u_1,u_2,...,u_n\}\).

The Orthogonalization goes as follows:

\[u_1 = v_1;\\ u_2 = v_2-\frac{(u_1,v_2)}{(u_1,u_1)}u_1;\\ u_3 = v_3-\frac{(u_1,v_3)}{(u_1,u_1)}u_1-\frac{(u_2,v_3)}{(u_2,u_2)}u_2;\\ \vdots\\ u_n = v_n-\frac{(u_1,v_n)}{(u_1,u_1)}u_1-\frac{(u_2,v_n)}{(u_2,u_2)}u_2-\cdots-\frac{(u_{n-1},v_n)}{(u_{n-1},u_{n-1})}u_{n-1}=v_n-\sum_{i=1}^{n-1}\frac{(u_i,v_n)}{(u_i,u_i)}u_i \]

Take \(u_2\) for example, the \(\frac{(u_1,v_2)}{(u_1,u_1)}u_1\) term is the projection of \(v_2\) on \(u_1\), and subtraction of this term from \(v_1\) makes the resultant vector \(u_2\) orthogonal to \(v_1\) since the projection part on \(v_1\)is elimmated from \(v_2\). Following this idea, we are able to achieve the orthogonalization.

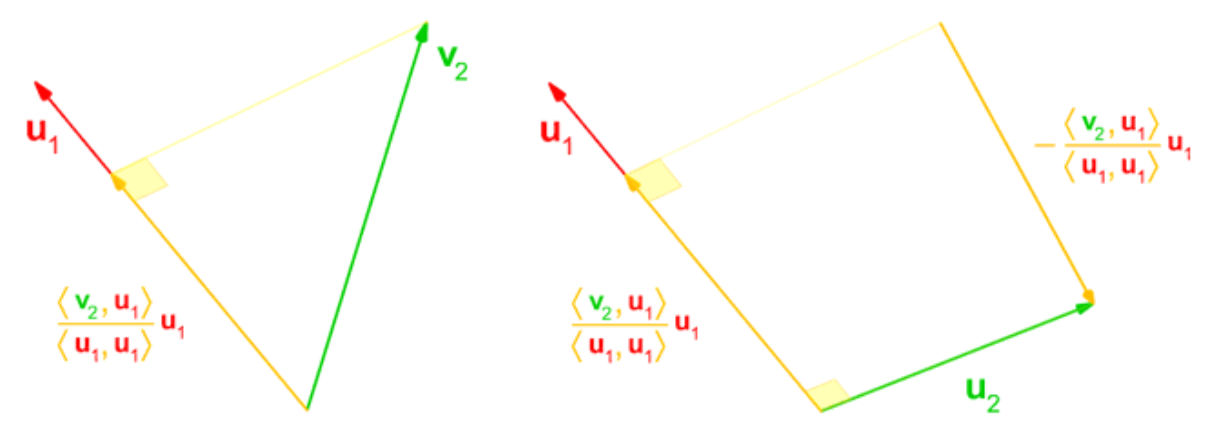
Then the normalization goes as follows:

\[e_i = \frac{u_i}{(u_i,u_i)^{1/2}} \]

Finally, we get a set of orthonormal vectors which is denoted by \(\{e_1,e_2,...,e_n\}\)