第五次程序4+（结对开发）

题目:返回一个整数数组中最大子数组的和。

要求：

输入一个整形数组，数组里有正数也有负数。

数组中连续的一个或多个整数组成一个子数组，每个子数组都有一个和。

如果数组A[0]……A[j-1]首尾相邻，允许A[i-1]，…… A[n-1]，A[0]……A[j-1]之和最大。

同时返回最大子数组的位置。

求所有子数组的和的最大值。

合作伙伴：

王文奇

博客链接：http://www.cnblogs.com/qwer111/

分析：这是在第四次程序的基础上再加了首尾链接，所以我在原先的基础上把输入的数组有重新在数组末尾再生成了一遍，在动态规划外围再加一个循环，从而实现计算A【0】-A【n]或者A【1】-A【n】-A[0]等等最大值计算，然后用一个数组记录最大值和还有起始地址和结尾地址。然后输出子数组。

代码：

//求一维数组的最大子数组 王文奇 缪金敏 2016/3/23
#include<iostream>
using namespace std;

int max(int a, int b)   //返回a和b中的最大值
{
    if (a > b)
    {
        return a;
    }
    else
    {
        return b;
    }
}

int main()
{
    int Array[10000];
    int i = 1,k;
    int dynamic_planning[10000][2], j, sum[10000];
    int start[10000] = {0};                   //最大子数组的起始位置  
    int end[10000] = { 0 };                    //最大子数组的终止位置  
    cout << "请输入一组一维数组(回车结束)：" << endl;
    cin >> Array[0];
    while (cin.get() != '\n') //回车结束
    {
        cin >> Array[i++];
    }
    for (j = i; j < 2 * i; j++) //数组末尾再生成了一遍
    {
        Array[j] = Array[j - i];
    }
    int n = 0;

    //动态规划数组初始化
    while (true){
        dynamic_planning[0][0] = 0;
        dynamic_planning[0][1] = Array[n];
        for (j = 1; j<i; j++)
        {
            dynamic_planning[j][0] = max(dynamic_planning[j - 1][0], dynamic_planning[j - 1][1]);
            dynamic_planning[j][1] = max(Array[j+n], (dynamic_planning[j - 1][1] + Array[j+n]));
            //开始下标的条件：数组第二列的数前一个比现在的小且小于0且第一列的数小于等于第二列
            if (dynamic_planning[j - 1][1] < dynamic_planning[j][1] && dynamic_planning[j - 1][1]<0 && dynamic_planning[j][0] <= dynamic_planning[j][1])
            {
                start[n] = j+n;
                //cout << "start:"<<start << endl;
            }
            //结束下标的条件1：当前的算出的最大子数组+输入的值比下一步的最大值大于或等于
            if (dynamic_planning[j - 1][1] >= dynamic_planning[j][0])
            {
                end[n] = j-1+n;
                //cout << "end:" << end << endl;
            }
            //结束下标的条件2：第二列的数大于等于第一列
            if (dynamic_planning[j][1] >= dynamic_planning[j][0])
            {
                end[n] = j+n;
                //cout << "end:" << end << endl;
            }

        }
        sum[n] = max(dynamic_planning[i - 1][0], dynamic_planning[i - 1][1]);
        n++;
        if (n == i)
        {
            break;
        }
    }
    int max = sum[0];
    n = 0;
    for (j = 0; j < i; j++)
    {
        if (sum[j]>max)
        {
            max = sum[j];
            n = j;
        }
    }
    cout << "最大的子数组为：" << endl;
    if (start[n] <= end[n])
    {
        for (j = start[n]; j <= end[n]; j++)
        {
            cout << Array[j] << " ";
        }
    }
    else
    {
        for (j = start[n]; j < i; j++)
        {
            cout << Array[j] << " ";
        }
        for (j = 0; j <= end[n]; j++)
        {
            cout << Array[j] << " ";
        }
    }
    cout << endl;
    cout << "起始索引： " << start[n];
    if (end[n] >= i)
        cout << "终止索引： " << end[n] - i;
    else
        cout << "终止索引： " << end[n];
    cout << endl;
    //cout << start << " " << end << endl;
    
    cout << "最大的子数组的和为：" << sum[n] << endl;
    return 0;
}

结果展示：

总结：

这一次练习只是在上一次基础上多加了一次循环，所以相对较为简单。

项目计划总结：

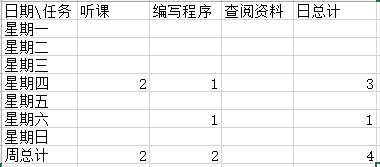
时间记录日志：

缺陷记录日志：