C语言质数判断

C语言质数判断

1.质数定义

质数 (素数）只能被 1 或自己整除。

同时它必须是大于 1 的整数。

1 不是质数也不是合成数。

常见的质数就是：2，3，5，7，11，13，17……

2. 判断质数方法

注意：为保持简洁，下面的代码都不考虑1和2，默认输入参数是大于2的整数。

1 不是质数，2是质数。

如果需要判断1和2，只需要加这个外壳就行。

如果该数是质数（素数），IsPrime函数返回1；如果该数不是质数，IsPrime函数返回0。

// 默认num是正整数
int IsPrime(int num)
{
    if(num == 1)    
        return 0;    # 1不是质数
    if(num == 2){
        return 1;    # 2是质数
    }else{
        //...
    }
}

2.1 方法一：除以比自己小的数字

除以每个小于自己的数字，如果出现整除，那肯定不是质数。

// 默认num是大于2的正整数
int IsPrime(int num)
{
	for (int i = 2; i < num; i++) {
		if (num % i == 0) {
            return 0;
        }
	}
	return 1;
}

或许，有的小伙伴会想到，如果 num 是大于2的偶数，肯定不是质数，直接返回1 不是会更快么。

加上个

if(num % 2 == 0)
    return 0;

变成这样：

// 默认num是大于2的正整数
int IsPrime(int num)
{
    if(num % 2 == 0)
        return 0;
	for (int i = 2; i < num; i++) {
		if (num % i == 0) {
            return 0;
        }
	}
	return 1;
}

我一开始也犯了这个错误。其实不需要加上偶数的判断，因为在 for 循环里面的 i = 2 时就已经达到了判断这个数字是否偶数的目的。

所以 我们加上的 num % 2 == 0 是多余的。

2.3 进一步：除以一半的数字

我们可以缩小 i 的范围，没有必要把所有比自己小的数字都来测试一遍，只需要用其中一半来测试就够了。

比如，num是13，我们只需要用 13/2，13/3，13/4，13/5，13/6即可。

// 默认num是大于2的正整数
int IsPrime(int num)
{
	for (int i = 2; i < (num / 2); i++) {
		if (num % i == 0) {
            return 0;
        }
	}
	return 1;
}

2.4 更进一步：除以更少的数字

其实，只需尝试更少的数字，只需要判断到 num 的平方根即可。

C语言的库函数 sqrt(num)就是求 num的平方根，sqrt(num) 表示 num 的平方根值。

因为如果一个数可以分解为两个数的乘积的情况下，则一定是一个数在sqrt（n）的左侧，一个数在sqrt（n）的右侧，或者两数相等，均为sqrt（n）。因此，判断sqrt（n）左侧的数即可，判断其能否被n整除。

// 默认num是大于2的正整数
// 注意：需要引入math头文件
#include <math>
int IsPrime(int num)
{
	for (int i = 2; i <= sqrt(num); i++) {
		if (num % i == 0) {
            return 0;
        }
	}
	return 1;
}

2.6 孪生质数

比较难理解，见下面链接。

【算法】素数(质数)判断方法_余 一的博客-CSDN博客_判断素数

2.7 获取范围内的所有质数：埃拉托斯特尼筛法

埃拉托斯特尼筛法（sieve of Eratosthenes ）用来找出一定范围（n）内的所有质数。其方法是从 2 开始，在 sqrt(n) 以内，将每个质数的倍数剔除掉，剩下的就是所求范围的质数。例如找 100 以内的质数，先把 2 的倍数筛掉（保留 2），再把 3 的倍数筛掉（保留 3），如此重复下去，直到 7 的倍数被筛掉（因为下一个质数 11 已经大于sqrt(100)，剩下的就是 100 以内的质数。

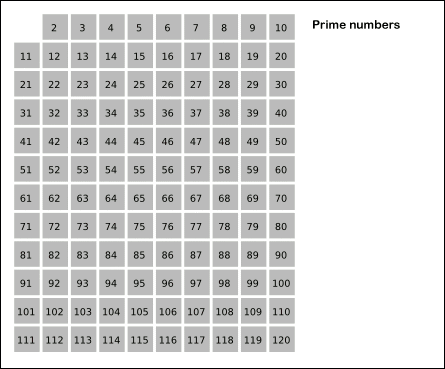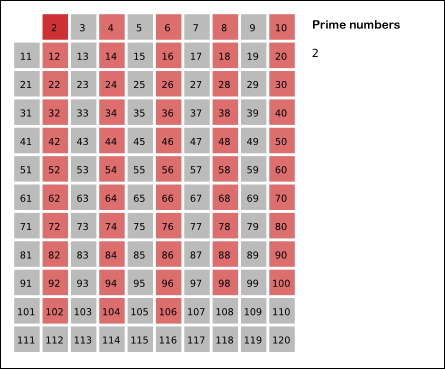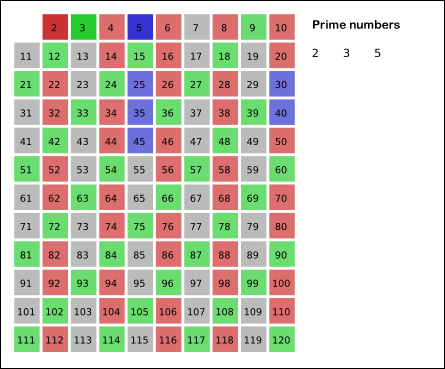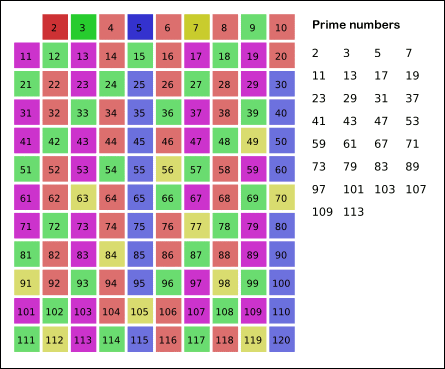
简单易懂，适合找到一定范围内的所有质数或者质数个数。