莫队算法
莫队算法
莫队,是莫涛发明的一种解决区间查询等问题的离线算法,基于分块思想,复杂度为\(O(n\sqrt{n})\) 。本文只涉及普通莫队。
一般来说,如果可以在 \(O(1)\) 内从 \([l,r]\) 的答案转移到 \([l-1,r]\) 、 \([l+1,r]\) 、 \([l,r-1]\) 、 \([l,r+1]\) 这四个与之紧邻的区间的答案,则可以考虑使用莫队。例如下面这个(几乎是莫队模板的)题目:
Given a sequence of n numbers \(a_1,a_2,\dots,a_n\)and a number of d-queries. A d-query is a pair (i, j) (1 ≤ i ≤ j ≤ n). For each d-query (i, j), you have to return the number of distinct elements in the subsequence ai, ai+1, ..., aj.
Input
Line 1: n (1 ≤ n ≤ 30000).
Line 2: n numbers \(a_1,a_2,\dots,a_n(1<a_i<10^6)\) .
Line 3: q (1 ≤ q ≤ 200000), the number of d-queries.
In the next q lines, each line contains 2 numbers i, j representing a d-query (1 ≤ i ≤ j ≤ n).
Output
For each d-query (i, j), print the number of distinct elements in the subsequence \(a_i,a_{i+1},\dots,a_j\) in a single line.
大意是,给出一个序列和若干查询l, r,问[l, r]中有多少个不同的数。这道题也可以用树状数组或块状数组来做,但用莫队的话思维难度会比较低。
之前说过,我们要把一个区间的答案转移到与之相邻的区间中去,怎么做呢?我们用一个数组Cnt[]来记录每个数出现的次数,cur 表示当前区间的答案,例如:
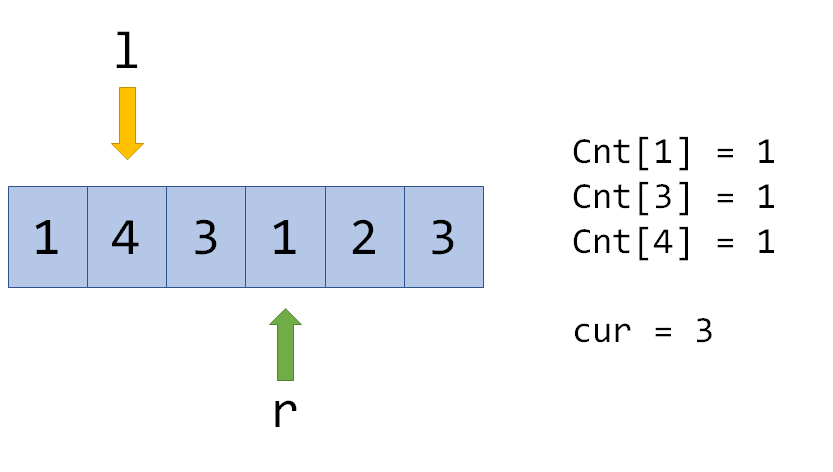
现在转移到紧邻的区间就很简单了,例如转移到[l,r+1]:
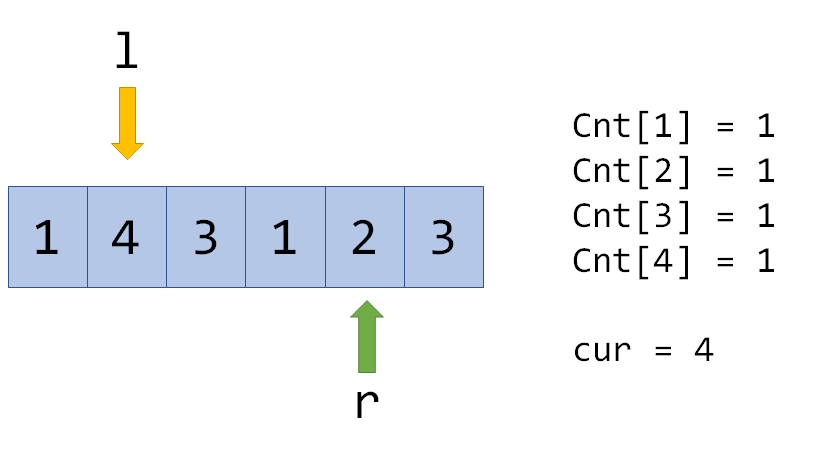
Cnt[2]=0,说明添加了一个没出现过的数,所以cur变成4,但如果在这里再次向右转移:
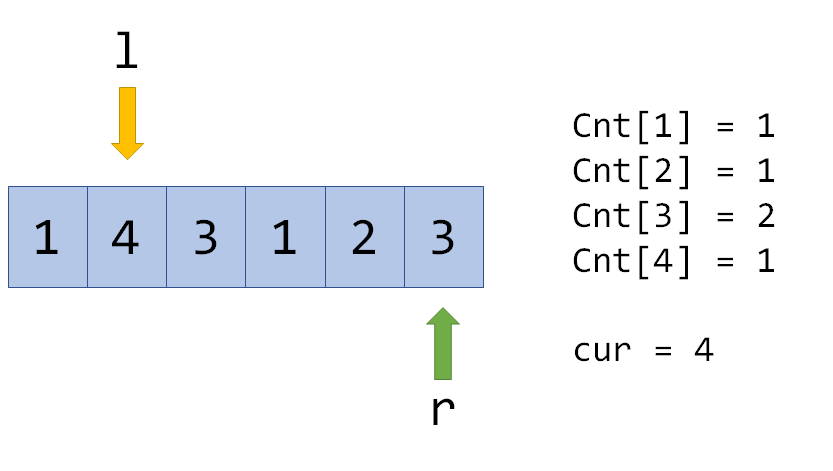
这时Cnt[3]不为0,所以虽然Cnt[3]++,但是cur不再增长。
其他的转移都是类似的。容易发现,转移分为两种情况,往区间里添数,或者往区间里删数,所以可以写成两个函数:
inline void add(int p) // 添数,p为下标
{
if (Cnt[A[p]] == 0)
cur++;
Cnt[A[p]]++;
}
inline void del(int p) // 删数
{
Cnt[A[p]]--;
if (Cnt[A[p]] == 0)
cur--;
}
那么从任意一个区间移动到另一个区间,只需写:
while (l > Q[i].l)
add(--l);
while (l < Q[i].l)
del(l++);
while (r < Q[i].r)
add(++r);
while (r > Q[i].r)
del(r--);
注意++和--的位置。删数是先删后移,添数是先移后添。初始化时,要先令l=1,r=0。
现在我们可以从一个区间的答案转移到另一个区间了,但是,如果直接在线查询,很有可能在序列两头“左右横跳”,到头来还不如朴素的 �(�2) 算法。但是,我们可以把查询离线下来(记录下来),然后,排个序……
问题来了,怎么排序?我们很容易想到以l为第一关键词,r为第二关键词排下序,但这样做效果并不是很好。莫涛大神给出的方法是,分块,然后按照bel[l] 为第一关键词,bel[r]为第二关键词排序。 这样,每两次询问间l和r指针移动的距离可以被有效地降低,整个算法的时间复杂度可以降到 �(��) !(这里不证了,这篇博客写的很好)
但在此之上,我们还可以进行常数优化:奇偶化排序。意为:如果bel[l] 是奇数,则将r顺序排序,否则将r逆序排序。 这为什么有效?如果按照一般的排序方法,指针的动向可能是这样的:
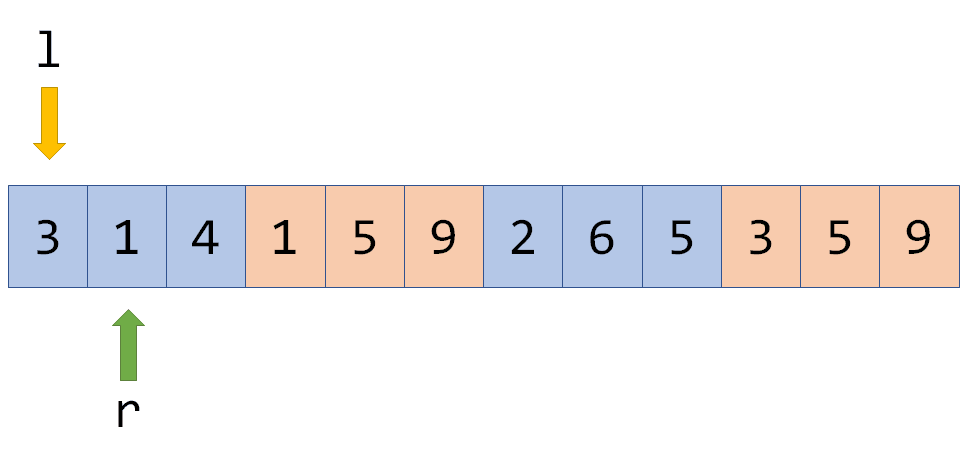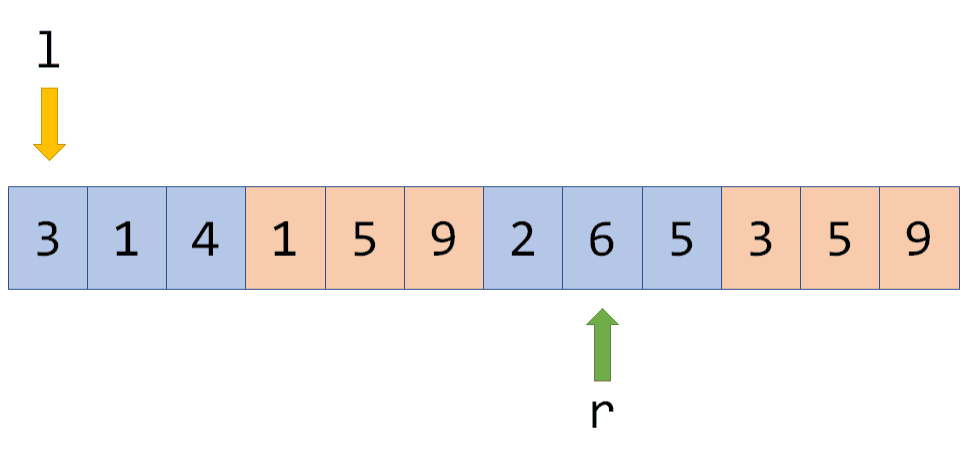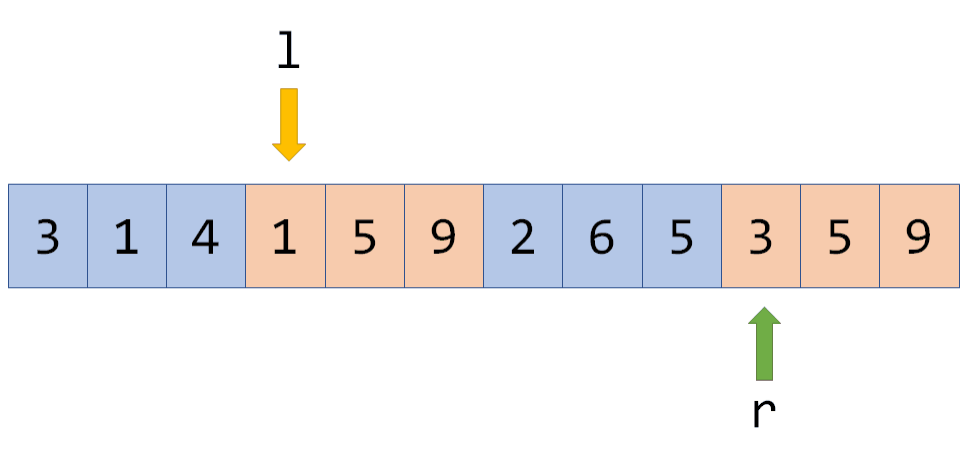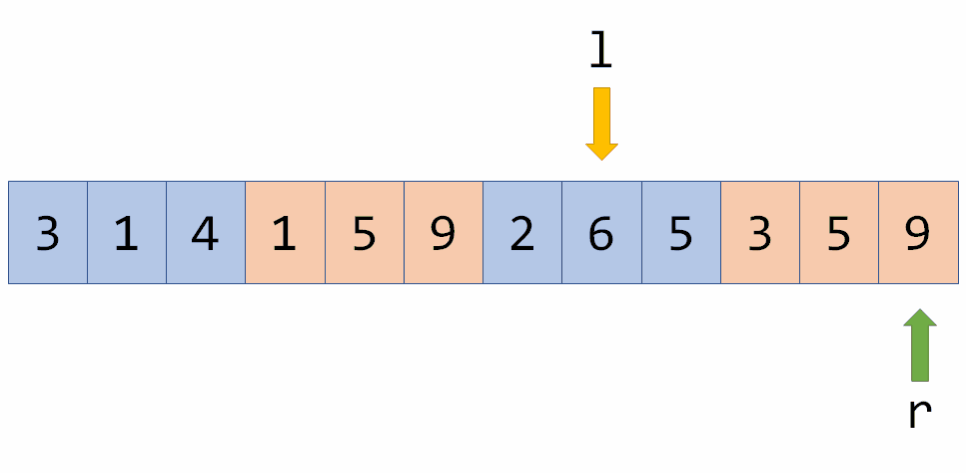
我们看到,每次l跨过一个块时,r都必须往左移很长一截。
而奇偶化排序后,指针的动向会变为这样:

可以发现,如果l在偶数块,r指针会在返回的“途中”就解决问题。
这就是普通莫队算法,给出上面那道例题的主要代码:
const int MAXN = 30005, MAXQ = 200005, MAXM = 1000005;
int sq;
struct query // 把询问以结构体方式保存
{
int l, r, id;
bool operator<(const query &o) const // 重载<运算符,奇偶化排序
{
// 这里只需要知道每个元素归属哪个块,而块的大小都是sqrt(n),所以可以直接用l/sq
if (l / sq != o.l / sq)
return l < o.l;
if (l / sq & 1)
return r < o.r;
return r > o.r;
}
} Q[MAXQ];
int A[MAXN], ans[MAXQ], Cnt[MAXM], cur, l = 1, r = 0;
inline void add(int p)
{
if (Cnt[A[p]] == 0)
cur++;
Cnt[A[p]]++;
}
inline void del(int p)
{
Cnt[A[p]]--;
if (Cnt[A[p]] == 0)
cur--;
}
int main()
{
int n = read();
sq = sqrt(n);
for (int i = 1; i <= n; ++i)
A[i] = read();
int q = read();
for (int i = 0; i < q; ++i)
Q[i].l = read(), Q[i].r = read(), Q[i].id = i; // 把询问离线下来
sort(Q, Q + q); // 排序
for (int i = 0; i < q; ++i)
{
while (l > Q[i].l)
add(--l);
while (r < Q[i].r)
add(++r);
while (l < Q[i].l)
del(l++);
while (r > Q[i].r)
del(r--);
ans[Q[i].id] = cur; // 储存答案
}
for (int i = 0; i < q; ++i)
printf("%d\n", ans[i]); // 按编号顺序输出
return 0;
}
记住,只要数据可离线(有些题目会要求强制在线,就不能用这个方法了)且可以在 \(O(1)\) 内实现转移,就可以用这个方法,而且很多时候只需要改一改add()和del()函数即可,相当简单。


