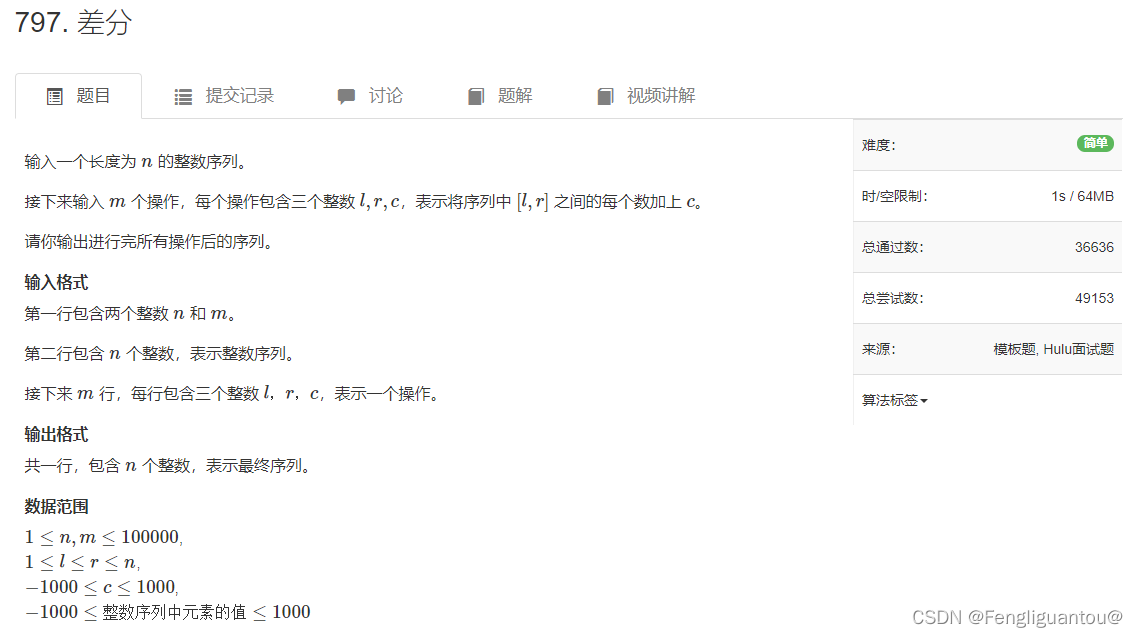
差分

差分算法

概念

在引出差分的概念之前，先看如下的两个数组

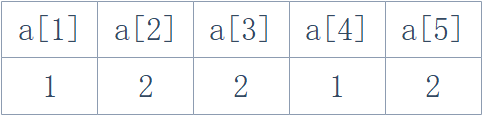
其差分数组为：

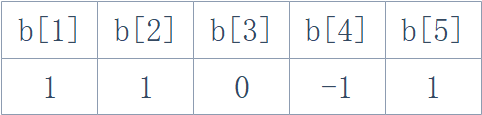
可以观察出a数组其实是b数组的前缀和
a[1]=b[1]
a[2]=b[1]+b[2]
a[3]=b[1]+b[2]+b[3]
a[4]=b[1]+b[2]+b[3]+b[4]…
a[i]=b[1]+b[2]+b[3]…+b[i-1]+b[i]
满足这样关系的数组，我们就称作差分数组，由此也可以看出差分其实是前缀和的逆运算。

前缀和与差分的关系

一维数组的差分

在某种场景下，题目可能会要求你让一个数组的任意一个区间+上一个数字，这时如果用到差分的思想，就可以做到快速求解。

差分数组的本质：

应用一：如何构造一个差分数组（前提条件：a已知，原a-b）：
核心公式：b[l]+= c; b[r+1] -= c;

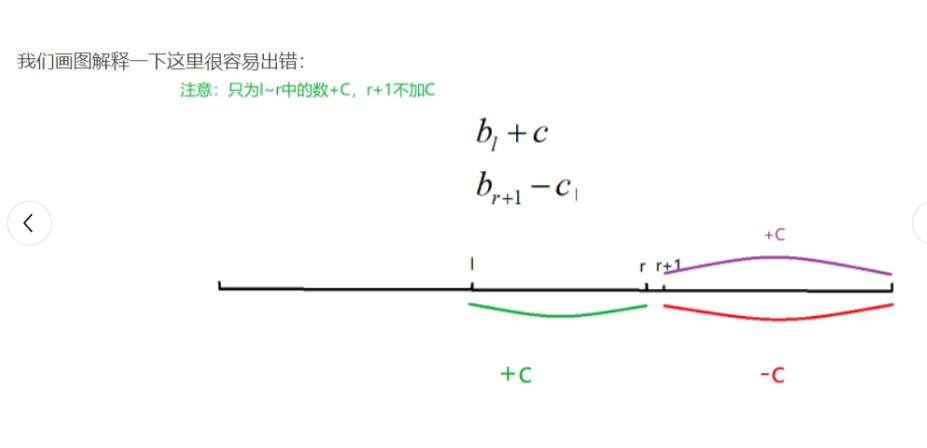
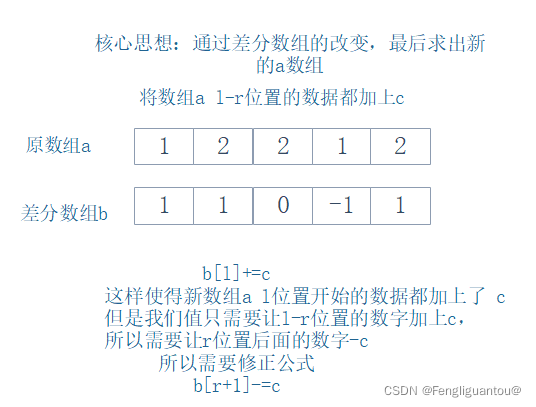
代码：

#include<bits/stdc++.h>
using namespace std;
const int N=100010;//N表示数组中元素个数
int a[N]={0},b[N]={0};//定义两个数组，原数组，差分数组
int n;//n表示数组中实际放了多少个元素

void insert(int l,int r,int c ){  //l=i;r=i;c=a[i]
    b[l]+=c;
    b[r+1]-=c;
}


int main(){
    scanf("%d",&n);
    for(int i=1;i<=n;i++)//往数组里放数，此时a[i]已知，作为原数组
    scanf("%d",&a[i]);
    
    for(int i=1;i<=n;i++)//构建一个差分数组
    insert(i,i,a[i]);
    
    for(int i=1;i<=n;i++)
    	printf("%d ",b[i]);
    
    return 0;
 }//此时相当于没有区间

应用二：通过差分数组对原数组的任意区间数据进行修改
假设需要修改原数组l-r这个区间的数据
一共两个步骤

步骤1： 构建差分数组

步骤2： 通过公式对差分数组进行修改
公式：b[l]+=c ; b[r+1]-=c;
步骤3： 通过修改以后的差分数组求出新的原数组
推导过程：

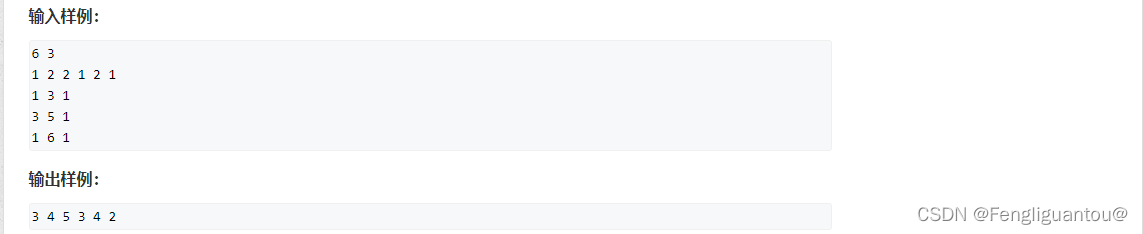
#include<bits/stdc++.h>

using namespace std;
const int N=100010;
int a[N],b[N];
int n,m;

void insert(int l,int r,int c ){
    b[l]+=c;
    b[r+1]-=c;
}

int main(){
    
    scanf("%d%d",&n,&m);
    
    for(int i=1;i<=n;i++)
    	scanf("%d",&a[i]);
    
    for(int i=1;i<=n;i++)
    	insert(i,i,a[i]);//(1)同上，构建差分数组
    
//---------------------------------------------------------//
    
    while(m--){//m个操作，相当于m个区间，也就是要进行m次区间加c,所以循环条件是m--
        int l,r,c;
        scanf("%d%d%d",&l,&r,&c);
        insert(l,r,c);//(2)//对差分数组进行m次区间加c
    }
    
    
    for(int i=1;i<=n;i++)//(3)//通过循环再求前n项和
        b[i]=b[i-1]+b[i];
    
    for(int i=1;i<=n;i++)
    	printf("%d ",b[i]);
    
    return 0;
}

(1)构造原数组的差分数组
(2)对差分数组进行数据修改
(3)通过差分数组得出新修改后的原数组