杨辉三角
C++编程 杨辉三角
杨辉三角
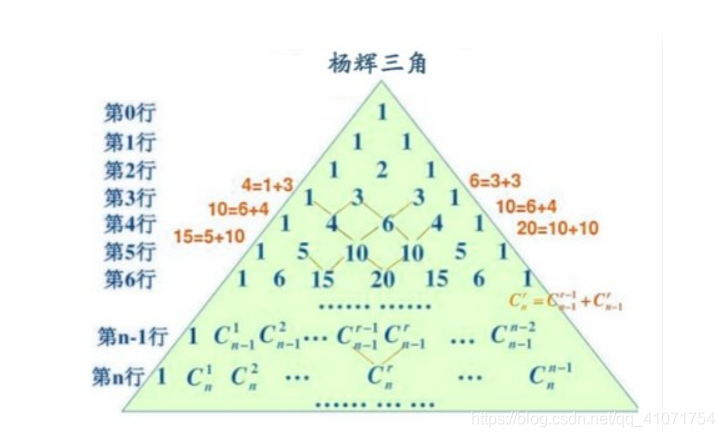
杨辉三角,是二项式系数在三角形中的一种几何排列。在欧洲,这个表叫做帕斯卡三角形。帕斯卡(1623----1662)是在1654年发现这一规律的,比杨辉要迟393年,比贾宪迟600年。杨辉三角是中国古代数学的杰出研究成果之一,它把二项式系数图形化,把组合数内在的一些代数性质直观地从图形中体现出来,是一种离散型的数与形的结合。
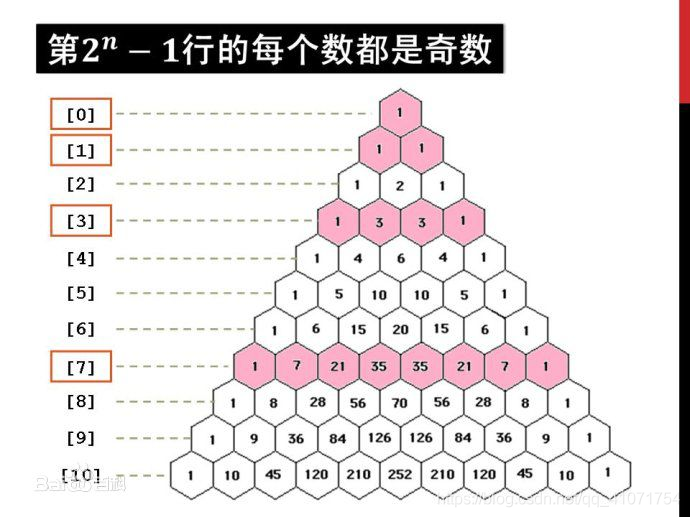
杨辉三角的特点:
(与上图中的n不同,这里第一行定义为n=1)
- 每个数等于它上方两数之和。
- 每行数字左右对称,由1开始逐渐变大。
- 第n行的数字有n项。
- 前n行共[(1+n)n]/2 个数。
- 第n行的m个数可表示为 C(n-1,m-1),即为从n-1个不同元素中取m-1个元素的组合数。
- 第n行的第m个数和第n-m+1个数相等 ,为组合数性质之一。
- 每个数字等于上一行的左右两个数字之和。可用此性质写出整个杨辉三角。即第n+1行的第i个数等于第n行的第i-1个数和第i个数之和,这也是组合数的性质之一。即
C(n+1,i)=C(n,i)+C(n,i-1)。 - (a+b)n的展开式中的各项系数依次对应杨辉三角的第(n+1)行中的每一项。
- 将第2n+1行第1个数,跟第2n+2行第3个数、第2n+3行第5个数……连成一线,这些数的和是第4n+1个斐波那契数;将第2n行第2个数(n>1),跟第2n-1行第4个数、第2n-2行第6个数……这些数之和是第4n-2个斐波那契数。
……
第一种实现形式:
【二维数组实现杨辉三角 输出10行】
#include <iostream>
#include <iomanip>
using namespace std;
/*杨辉三角最终显示效果是一个等腰三角形,两个最外边都是1
杨辉三角的根本在于,每个数等于它上方两数之和
*/
int main(){
const int n=11;//变量n在此处起到了限制输出行数的作用,可优化成用户输入
int i,j,a[n][n];
//使第一列和对角线元素的值为1
for (i=1;i<n;i++){ //前两行全为1,拿出来单独处理
a[i][i]=1;//使最右侧边全为1
a[i][1]=1;//使最左侧边全为1
}
//从第三行开始处理
for (i=3;i<n;i++) //三行开始出现变化
for (j=2;j<=i-1;j++) //j始终慢i一步
a[i][j]=a[i-1][j-1]+a[i-1][j];//每个数等于它上方两数之和,如a32=a21+a22
//输出数组各元素的值
for (i=1;i<n;i++){ //从第一行开始
for (j=1;j<=i;j++) //利用j将每一行的数据全部输出
cout<<setw(5)<<a[i][j]<<" "; //在C++中,setw(int n)用来控制输出间隔,这里是指前元素末尾与后元素末尾之间有个5空格位
cout<<endl;
}
cout<<endl;
return 0;
}
效果展示图
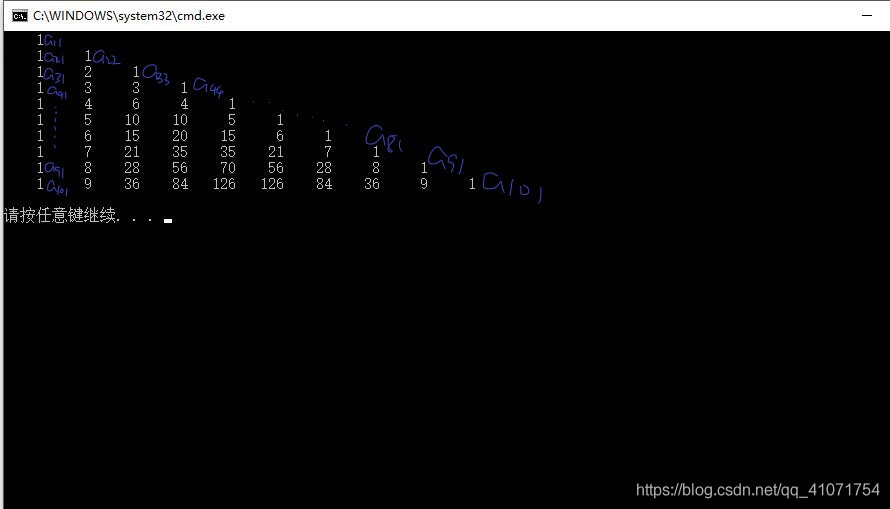
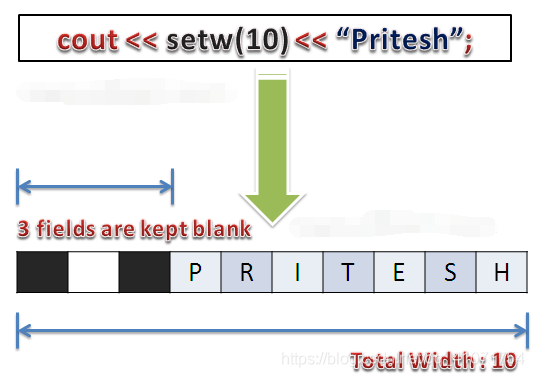
PS1:setw()函数的使用:
C++函数std::setw的行为与在流上调用n作为参数的成员宽度一样,它作为操纵器插入/提取(在输入流或输出流上插入/提取)。
它用于设置要在输出操作上使用的字段宽度。
特点:
-
setw()是C ++中的库函数。
-
setw()在#include <iomanip.>中声明
-
setw()将设置字段宽度。
-
setw()设置要用作 下一个插入操作的字段宽度的字符数 。
PS2:*std是什么意思?*
在C++中,std其实就是standard标准的意思,std是一个类(输入输出标准),它包括了cin成员和cout成员,using name space std ;以后才能使用它的成员。
例如std::cin就是标准输入,std::cout就是标准输出的意思。
#include <iostream.>,它包含了一个类,在类的使用之前要预处理一下,using namespace std;就是这个功能,然后你就可以使用cin,cout这两个成员函数了,假设你不使用预处理(using namespace std;),就需要加上加上std::cin或者std::cout再去使用它的成员函数。
参考资料:
【百度知道】C++中"std::"是什么意思?
第二种实现形式:
【指针动态开辟空间,一维数组实现杨辉三角 输出任意行】
该方法使用灵活,但是理解略显困难。
#include <iostream>
#include <iomanip>
using namespace std;
int* YangHuiData(int n); //n是杨辉三角形的行数
void YangHuiShow(int *pData, int n);//在屏幕上打印杨辉三角形
int main() {
int n;
cout << "请输入杨辉三角形的行数";
cin >> n;
//计算杨辉三角并保存到二维数组
int *pData = YangHuiData(n);
//在屏幕上打印等腰三角形的杨辉三角
YangHuiShow(pData, n);
//n是杨辉三角形的行数
}
int* YangHuiData(int n) {
int *a = new int[n*n]; 用指针a指向new动态分配的长度为(n*n)*sizeof(int)的内存空间
//完成杨辉三角形的计算,没有显示的位置填0
int i, j;
for (i = 0; i<n*n; i++) {
a[i] = 0; //填0操作
}
a[0] = 1;
a[n] = 1;
a[n + 1] = 1;
for (i = 2; i<n; i++) {
a[i*n] = 1;
a[i*n + i] = 1;
for (j = 1; j<i; j++) {
a[i*n + j] = a[(i - 1)*n + j - 1] + a[(i - 1)*n + j]; //通过a[i*n+j]来访问第(i*n+j)个数据,根据杨辉三角的特性求值
}
}
return a;
}
void YangHuiShow(int *a, int n) {
//根据数据a指向的二维数组在屏幕上打印
//杨辉三角形,每行前面填充合适的空格
//以显示成等腰三角形,左右对称
int i, j;
for (i = 0; i<n; i++)
{
for (j = 0; j<n - i - 1; j++)
cout << setw(3) << " ";//前导空格,为单个数据的一半宽度
for (j = 0; j <= i; j++)
cout << setw(6) << a[i*n + j];
cout << endl;
}在这里插入图片描述
}
代码分析图(以3x3为例)

效果展示图
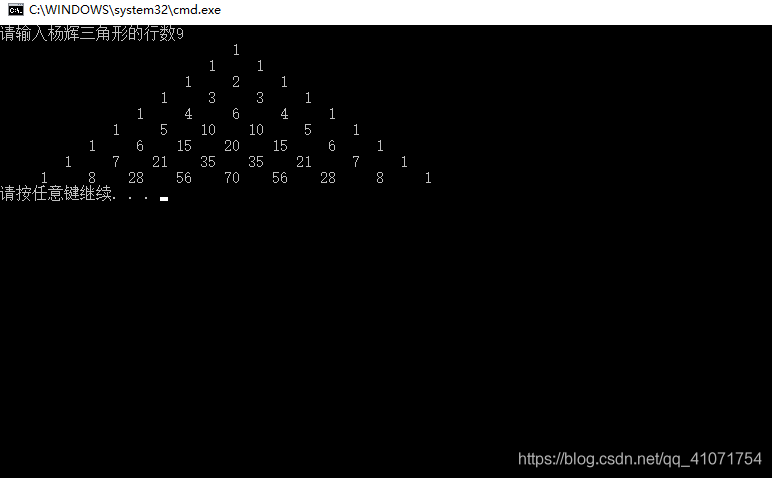
PS3:C++中如何正确的开辟一个动态的二维数组:
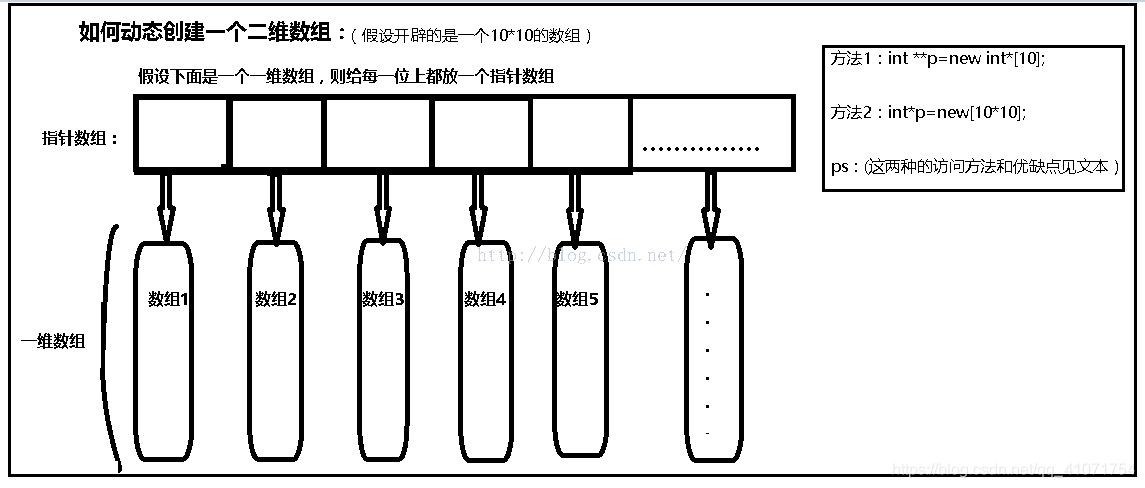
两种定义二维数组的方式,访问数据的方式,优缺点:
方法一:
定义方式:
int **p=new int*[10];
for (int i=0;i<=10;++i)
{
p[i]=new int[10];
}
访问数据的方式:直接通过a[i][j]访问第i行第j列的数据。
优缺点:通过a[i][j]访问数据容易,但是new的次数太多,释放空间不容易。
方法二:
定义方式:
int *p=new int[10*10];(ps:这种事当成一维数组连续开辟的。)
访问数据的方式:通过a[i*10+j]来访问第(i*10+j)个数据。
优缺点:访问数据很方便,且new的次数少,释放空间容易,但是不便于理解。
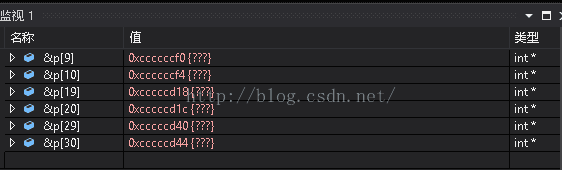
*图例:(看&p[9]和&p[10]等地址相差为4个字节,即它们是相连的,所以为一维数组)
参考资料:
【转载于 ycz_csdn】C++中如何正确的开辟一个动态的二维数组
参考资料:
【百度百科】杨辉三角
【coolsunxu】C++编写杨辉三角
【数学之美】杨辉三角(帕斯卡三角)的奇特性质
【百度经验】用例子理解排列组合及基本公式如何计算


