【转】数论——Lucas定理模板

For non-negative integers m and n and a prime p, the following congruence relation holds:

\binom{m}{n}\equiv\prod_{i=0}^k\binom{m_i}{n_i}\pmod p,

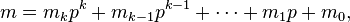
wherem=m_kp^k+m_{k-1}p^{k-1}+\cdots +m_1p+m_0,

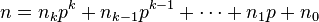
andn=n_kp^k+n_{k-1}p^{k-1}+\cdots +n_1p+n_0

are the base p expansions of m and n respectively.

 

 1 #include <iostream>
 2 #include <cstdio>
 3 #include <cstring>
 4 usingnamespace std;
 5 
 6 typedef longlong llg;
 7 
 8 constint N =150000;
 9 
10 llg n, m, p, fac[N];
11 
12 void init()
13 {
14     int i;
15     fac[0] =1;
16     for(i =1; i <= p; i++)
17         fac[i] = fac[i-1]*i % p;
18 }
19 
20 llg pow(llg a, llg b)
21 {
22     llg tmp = a % p, ans =1;
23     while(b)
24     {
25         if(b &1)  ans = ans * tmp % p;
26         tmp = tmp*tmp % p;
27         b >>=1;
28     }
29     return  ans;
30 }
31 
32 llg C(llg n, llg m)
33 {
34     if(m > n)  return0;
35     return  fac[n]*pow(fac[m]*fac[n-m], p-2) % p;
36 }
37 
38 llg Lucas(llg n, llg m)
39 {
40     if(m ==0)  return1;
41     elsereturn  (C(n%p, m%p)*Lucas(n/p, m/p))%p;
42 }
43 
44 int main()
45 {
46     int t;
47     scanf("%d", &t);
48     while(t--)
49     {
50         scanf("%I64d%I64d%I64d", &n, &m, &p);
51         init();
52         printf("%I64d\n", Lucas(n+m, n));
53     }
54     return0;
55 }

 

 

posted on 2012-08-19 13:36  miao11621  阅读(321)  评论(0)  编辑  收藏  举报

导航