DS博客作业03--树
| 这个作业属于哪个班级 | 数据结构--网络2011/2012 |
| ---- | ---- | ---- |
| 这个作业的地址 | DS博客作业03--树 |
| 这个作业的目标 | 学习树结构设计及运算操作 |
| 姓名 |廖浩轩|
0.PTA得分截图

1.本周学习总结
1.1 二叉树结构
1.1.1 二叉树的2种存储结构
顺序存储结构:
把一个满二叉树自上而下、从左到右顺序编号,依次存放在数组内,可得到图6.8(a)所示的结果。设满二叉树结点在数组中的索引号为i,那么有如下性质。
(1)如果i = 0,此结点为根结点,无双亲。
(2)如果i > 0,则其双亲结点为(i -1) / 2 。(注意,这里的除法是整除,结果中的小数部分会被舍弃。)
(3)结点i的左孩子为2i + 1,右孩子为2i + 2。
(4)如果i > 0,当i为奇数时,它是双亲结点的左孩子,它的兄弟为i + 1;当i为偶数时,它是双新结点的右孩子,它的兄弟结点为i – 1。
(5)深度为k的满二叉树需要长度为2 k-1的数组进行存储。
通过以上性质可知,使用数组存放满二叉树的各结点非常方便,可以根据一个结点的索引号很容易地推算出它的双亲、孩子、兄弟等结点的编号,从而对这些结点进行访问,这是一种存储二叉满二叉树或完全二叉树的最简单、最省空间的做法。
为了用结点在数组中的位置反映出结点之间的逻辑关系,存储一般二叉树时,只需要将数组中空结点所对应的位置设为空即可,其效果如图6.8(b)所示。这会造成一定的空间浪费,但如果空结点的数量不是很多,这些浪费可以忽略。
一个深度为k的二叉树需要2 k-1个存储空间,当k值很大并且二叉树的空结点很多时,最坏的情况是每层只有一个结点,再使用顺序存储结构来存储显然会造成极大地浪费,这时就应该使用链式存储结构来存储二叉树中的数据。
#define Maxsize 100
typedef struct TNode {
char tree[Maxsize]; //数组存放二叉树中的节点
int parent; //表示双亲结点的下标
}TNode, * BTree;
链式存储结构:
二叉树的链式存储结构可分为二叉链表和三叉链表。二叉链表中,每个结点除了存储本身的数据外,还应该设置两个指针域left和right,它们分别指向左孩子和右孩子(如图6.9(a)所示)。
当需要在二叉树中经常寻找某结点的双亲,每个结点还可以加一个指向双亲的指针域parent,如图6.9(b)所示,这就是三叉链表。
二叉树还有一种叫双亲链表的存储结构,它只存储结点的双亲信息而不存储孩子信息,由于二叉树是一种有序树,一个结点的两个孩子有左右之分,因此结点中除了存放双新信息外,还必须指明这个结点是左孩子还是右孩子。由于结点不存放孩子信息,无法通过头指针出发遍历所有结点,因此需要借助数组来存放结点信息。图6.10(a)所示的二叉树使用双亲链表进行存储将得到图6.11所示的结果。由于根节点没有双新,所以它的parent指针的值设为-1。
双亲链表中元素存放的顺序是根据结点的添加顺序来决定的,也就是说把各个元素的存放位置进行调换不会影响结点的逻辑结构。由图6.11可知,双亲链表在物理上是一种顺序存储结构。
二叉树存在多种存储结构,选用何种方法进行存储主要依赖于对二叉树进行什么操作来确定。而二叉链表是二叉树最常用的存储结构,下面几节给出的有关二叉树的算法大多基于二叉链表存储结构。
typedef struct TNode { //二叉树结点由数据域,左右指针组成
char data;
struct TNode* lchild;
struct TNode* rchild;
}TNode, * BTree;
1.1.2 二叉树的构造
二叉树构造:顺序存储结构转二叉链,先序遍历,先序+中序序列,中序+后序序列
先序+中序序列:前序遍历第一位数字一定是这个二叉树的根结点。中序遍历中,根结点讲序列分为了左右两个区间。左边的区间是左子树的结点集合,右边的区间是右子树的结点集合。
void CreateTree(BiTree& T, char* pre, char* infix, int n)
{
int i;
char* pi;
if (n <= 0)
{
T = NULL;
return;
}
T = new BiTNode;
T->data = *pre;
for (pi = infix; pi < infix + n; pi++)
{
if (*pi == T->data)
{
break;
}
}
i = pi - infix;
CreateTree(T->lchild, pre+1, infix, i);
CreateTree(T->rchild, pre+i+1, pi + 1, n - i - 1);
}
中序+后序序列:找到根结点(后序遍历的最后一位)在中序遍历中,找到根结点的位置,划分左右子树,递归构建二叉树。思路和先序+中序序列遍历一样。
void CreateTree(BiTree& T, int* post, int* infix, int n)
{
int i;
int* pi;
if (n <= 0)
{
T = NULL;
return;
}
T = new BiTNode;
T->data = *(post + n - 1);
for (pi = infix; pi < infix + n; pi++)
{
if (*pi == *(post + n - 1))
{
break;
}
}
i = pi - infix;
CreateTree(T->lchild, post, infix, i);
CreateTree(T->rchild, post + i, pi + 1, n - i - 1);
}
1.1.3 二叉树的遍历
二叉树的遍历:前序,中序,后序,层次
前序:二叉树先序遍历的实现思想是:访问根节点;访问当前节点的左子树;若当前节点无左子树,则访问当前节点的右子树。
void PreOrderTraverse(BiTree T)
{
if (T)
{
cout<<T->data<<" ";
PreOrderTraverse(T->lchild);
PreOrderTraverse(T->rchild);
}
}
中序:二叉树中序遍历的实现思想是:访问当前节点的左子树;访问根节点;访问当前节点的右子树。
void INOrderTraverse(BiTree T)
{
if (T)
{
INOrderTraverse(T->lchild);
cout<<T->data<<" ";
INOrderTraverse(T->rchild);
}
}
后序:二叉树后序遍历的实现思想是:从根节点出发,依次遍历各节点的左右子树,直到当前节点左右子树遍历完成后,才访问该节点元素。
void PostOrderTraverse(BiTree T)
{
if (T)
{
PostOrderTraverse(T->lchild);
PostOrderTraverse(T->rchild);
cout<<T->data<<" ";
}
}
层次:层次遍历是从上到下、从左到右依次遍历每个结点。通过队列的应用,从根结点开始,将其左孩子和右孩子入队,然后根结点出队,重复次操作,直到队为空,出队顺序就是层次遍历的结果。
void LevelTravesal(BiTree T)
{
queue<BiTree>qu;
BiTree BT;
int flag = 0;
if (T == NULL)
{
cout << "NULL";
return;
}
qu.push(T);
while (!qu.empty())
{
BT = qu.front();
if (flag == 0)
{
cout << BT->data;
flag = 1;
}
else
{
cout << " " << BT->data;
}
qu.pop();
if (BT->lchild != NULL)
{
qu.push(BT->lchild);
}
if (BT->rchild != NULL)
{
qu.push(BT->rchild);
}
}
}
1.1.4 线索二叉树
线索二叉树:
二叉链存储结构时,每个结点都有两个指针,一共有2n个指针域,有效指针域为n-1个,空指针域有n+1个,可以利用空指针域指向该线性序列的前驱和后继指针,这称为线索。
若结点有左子树,则其lchild域指向左孩子,否则指向直接前驱;若结点有右子树,则其rchild域指向右孩子,否则指向直接后继。
为了避免混淆,再增加两个标志域LTag和RTag。若LTag=0,lchild域指向左孩子;若LTag=1,lchild域指向其前驱;若RTag=0,rchild域指向右孩子;若RTag=1,rchild域指向其后继。
存储结构
typedef struct Node
{
ElemType data;
int LTag,RTag;
struct Node *lchild,*rchild;
}TBTNode;
寻找结点前驱:观察线索二叉树的示意图,如果LTag=1,直接找到前驱,如果LTag=0,则走到该结点左子树的最右边的结点,即为要寻找的结点的前驱。
binThiTree* preTreeNode(binThiTree* q) {
binThiTree* cur;
cur = q;
if (cur->LTag == true) {
cur = cur->lchild;
return cur;
}
else{
cur = cur->lchild;//进入左子树
while (cur->RTag == false) {
cur = cur->rchild;
}//找到左子树的最右边结点
return cur;
}
}
寻找结点后继:观察线索二叉树示意图,如果RTag=1,直接找到后继,如果RTag=0,则走到该结点右子树的最左边的结点,即为要寻找的结点的后继。
binThiTree* rearTreeNode(binThiTree* q) {
binThiTree* cur = q;
if (cur->RTag == true) {
cur = cur->rchild;
return cur;
}
else {
//进入到*cur的右子树
cur = cur->rchild;
while (cur->LTag == false) {
cur = cur->lchild;
}
return cur;
}
}
1.1.5 二叉树的应用--表达式树
如图所示为表达式3x2+x-1/x+5的二叉树表示。树中的每个叶结点都是操作数,非叶结点都是运算符。
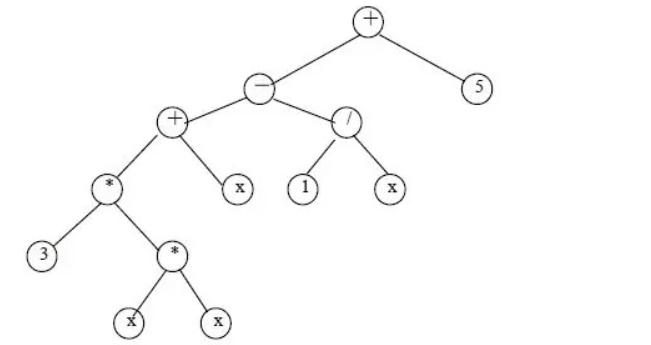
对该二叉树分别进行先序、中序和后序遍历,可以得到表达式的三种不同表示形式。
前缀表达式+-+3xxx/1x5
中缀表达式3xx+x-1/x+5
后缀表达式3xx**x+1x/-5+
表达式树的构建和输出
#include<stdio.h>
#include<string.h>
typedef struct binode
{
char data[4];
int h;
int depth;
struct binode *lchild,*rchild;
}binode,*bitree;
char d[100][100];
int q=0,num1;
void creatbitree(bitree &T,int y,int num)
{
if(d[q][0]=='#') {T=NULL;q++;}
else
{
T=new binode;
if(y==1) T->h=1;
else T->h=0;
T->depth=++num;
strcpy(T->data,d[q++]);
creatbitree(T->lchild,1,T->depth);
creatbitree(T->rchild,0,T->depth);
}
}
void travel(bitree T)
{
int i;
if(T!=NULL)
{
if(T->data[0]=='+'||T->data[0]=='-'||T->data[0]=='*'||T->data[0]=='/')
{
printf("(");
travel(T->lchild);
printf("%s",T->data);
travel(T->rchild);
printf(")");
}
else
printf("%s",T->data);
}
}
int ldepth(bitree T)
{
if(T==NULL)
return 0;
num1=ldepth(T->lchild);
return num1+1;
}
int rdepth(bitree T)
{
if(T==NULL)
return 0;
num1=rdepth(T->rchild);
return num1+1;
}
int main()
{
char a[500];
bitree T;
while(gets(a)!=NULL)
{
int i,j=0,k=0;
q=0;
for(i=0;a[i]!='\0';i++)
{
if(a[i]!=' ')
d[j][k++]=a[i];
else
{
d[j][k++]='\0';
//puts(d[j]);
k=0;
j++;
}
}
d[j++][k++]='\0';
//printf("%d\n",j);
creatbitree(T,2,0);
travel(T);
printf("\n");
}
}
1.2 多叉树结构
1.2.1 多叉树结构
多叉树是指一个父节点可以有多个子节点,但是一个子节点依旧遵循一个父节点定律,通常情况下,二叉树的实际应用高度太高,可以通过多叉树来简化对数据关系的描述。
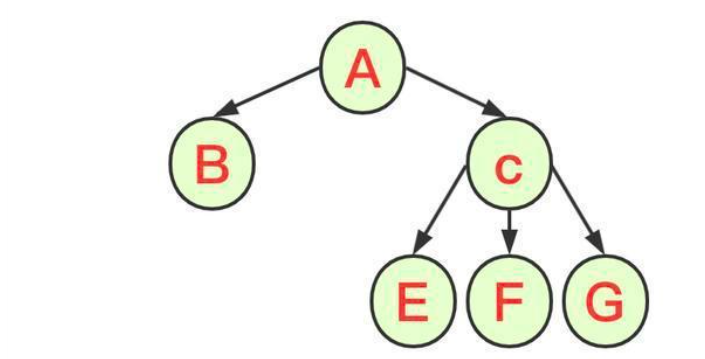
多叉树结构
typedef struct node_t
{
char* name; // 节点名
int n_children; // 子节点个数
int level; // 记录该节点在多叉树中的层数
struct node_t** children; // 指向其自身的子节点,children一个数组,该数组中的元素时node_t*指针
} NODE; // 对结构体重命名
1.2.2 多叉树遍历
给定一个 N 叉树,返回其节点值的前序遍历。
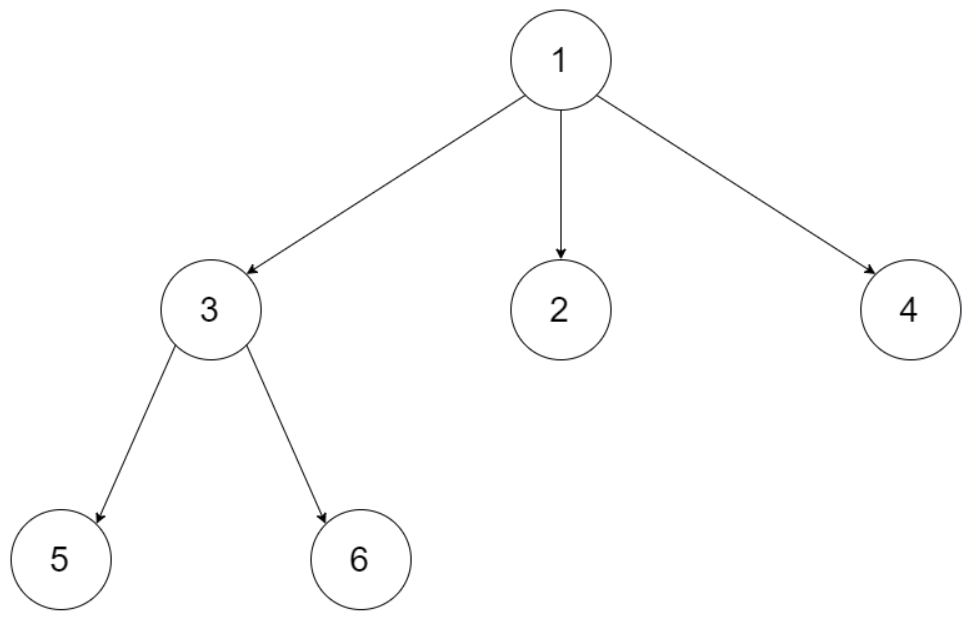
返回其前序遍历: [1,3,5,6,2,4]。
class Solution {
public List<Integer> res = new ArrayList<Integer>();
public List<Integer> preorder(Node root) {
if(root == null)
return res;
res.add(root.val);
for(Node child : root.children){
preorder(child);
}
return res;
}
1.3 哈夫曼树
1.3.1 哈夫曼树定义
哈夫曼树:给定N个权值作为N个叶子结点,构造一棵二叉树,若该树的带权路径长度达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树(Huffman Tree)。哈夫曼树是带权路径长度最短的树,权值较大的结点离根较近。
解决问题:
哈夫曼静态编码,哈夫曼动态编码
在数据通信中,需要将传送的文字转换成二进制的字符串,用0,1码的不同排列来表示字符。例如,需传送的报文为“AFTER DATA EAR ARE ART AREA”,这里用到的字符集为“A,E,R,T,F,D”,各字母出现的次数为{8,4,5,3,1,1}。现要求为这些字母设计编码。
1.3.2 哈夫曼树的结构体
typedef struct HuffmanTree
{
ELEMTYPE weight;
ELEMTYPE id; // id用来主要用以区分权值相同的结点,这里代表了下标
struct HuffmanTree* lchild;
struct HuffmanTree* rchild;
}HuffmanNode;
typedef struct{ //哈夫曼树结构体
int weight; //输入权值
int parent,lchild,rchild; //双亲节点,左孩子,右孩子
}HNodeType;
1.3.3 哈夫曼树构建及哈夫曼编码
哈夫曼树构建:
假设有n个权值,则构造出的哈夫曼树有n个叶子结点。 n个权值分别设为 w1、w2、…、wn,则哈夫曼树的构造规则为:
(1) 将w1、w2、…,wn看成是有n 棵树的森林(每棵树仅有一个结点);
(2) 在森林中选出两个根结点的权值最小的树合并,作为一棵新树的左、右子树,且新树的根结点权值为其左、右子树根结点权值之和;
(3)从森林中删除选取的两棵树,并将新树加入森林;
(4)重复(2)、(3)步,直到森林中只剩一棵树为止,该树即为所求得的哈夫曼树。
如下图做解释:
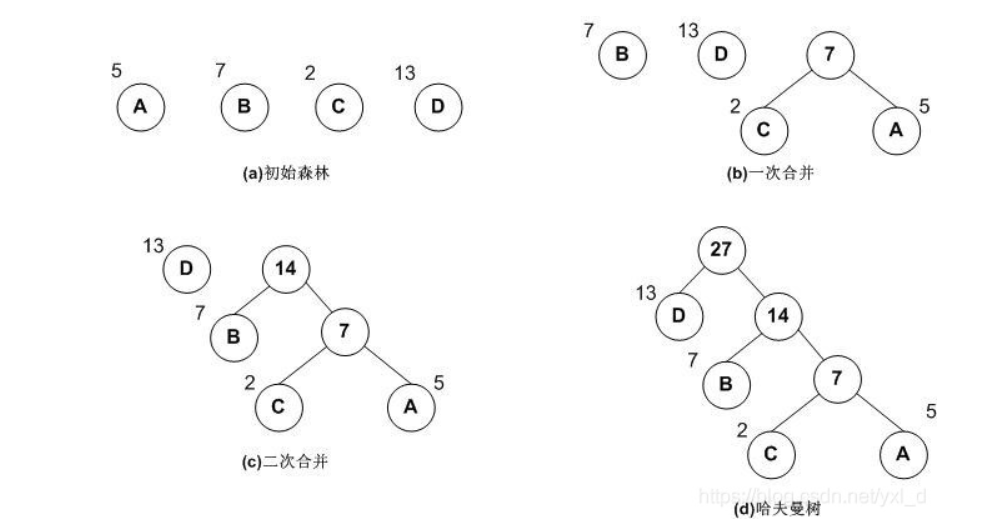
哈夫曼编码:
利用哈夫曼树求得的二进制编码称为哈夫曼编码。树中从根到每个叶子节点都有一条路径,对路径上的各分支约定指向左子树的分支表示”0”码,指向右子树的分支表示“1”码,取每条路径上的“0”或“1”的序列作为各个叶子节点对应的字符编码,即是哈夫曼编码。
如下图做解释:
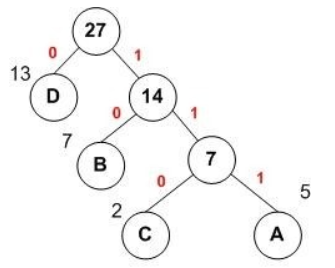
A,B,C,D对应的哈夫曼编码分别为:111,10,110,0
1.4 并查集
并查集:
并查集,在一些有N个元素的集合应用问题中,我们通常是在开始时让每个元素构成一个单元素的集合,然后按一定顺序将属于同一组的元素所在的集合合并,其间要反复查找一个元素在哪个集合中。这一类问题近几年来反复出现在信息学的国际国内赛题中。其特点是看似并不复杂,但数据量极大,若用正常的数据结构来描述的话,往往在空间上过大,计算机无法承受;即使在空间上勉强通过,运行的时间复杂度也极高,根本就不可能在比赛规定的运行时间(1~3秒)内计算出试题需要的结果,只能用并查集来描述。
并查集是一种树型的数据结构,用于处理一些不相交集合(disjoint sets)的合并及查询问题。常常在使用中以森林来表示。
结构体
typedef struct node
{
int data;
int rank;
int parent;
}UFSTree;
初始化
int fa[MAXN];
inline void init(int n)
{
for (int i = 1; i <= n; ++i)
fa[i] = i;
}
假如有编号为1, 2, 3, ..., n的n个元素,我们用一个数组fa[]来存储每个元素的父节点(因为每个元素有且只有一个父节点,所以这是可行的)。一开始,我们先将它们的父节点设为自己。
查询
int find(int x)
{
if(fa[x] == x)
return x;
else
return find(fa[x]);
}
我们用递归的写法实现对代表元素的查询:一层一层访问父节点,直至根节点(根节点的标志就是父节点是本身)。要判断两个元素是否属于同一个集合,只需要看它们的根节点是否相同即可。
合并
inline void merge(int i, int j)
{
fa[find(i)] = find(j);
}
合并操作也是很简单的,先找到两个集合的代表元素,然后将前者的父节点设为后者即可。
1.5 谈谈你对树的认识及学习体会
本章主要学习了树的结构,属于非线性结构。线性结构是一对一关系,而树结构是一对多的关系。树结构有二叉树,线索二叉树和哈夫曼树,二叉树由一个根节点和左子树和右子树组成。线索二叉树是利用空余的指针指向结点前驱,而哈夫曼树利用带权路径解决最优问题。树结构的运算大部分都是递归运算,所以只有用好递归才能更加的熟悉树的操作。一般递归体分为左子树和右子树,递归口为结点为空或者其他条件。对树结构有了一定的学习后,发现代码调试时很困难,因为有些复杂了,但也为多对多关系打了基础。
2.PTA实验作业
2.1 二叉树

2.1.1 解题思路及伪代码
int CalculateWpl(BTree bt,int h) //计算叶子结点带权路径长度和
if bt为空 do
return 0
end if
if bt->lchild为空 and bt->rchild为空 do //叶子结点
return bt->data*h //bt->data要转化为整型
end if
return 递归左子树和右子树
2.1.2 总结解题所用的知识点
递归遍历每个结点,碰到叶子结点计算wpl大小,算出最后总的wpl值
主要就是wpl值的计算和树结点的遍历
2.2 目录树
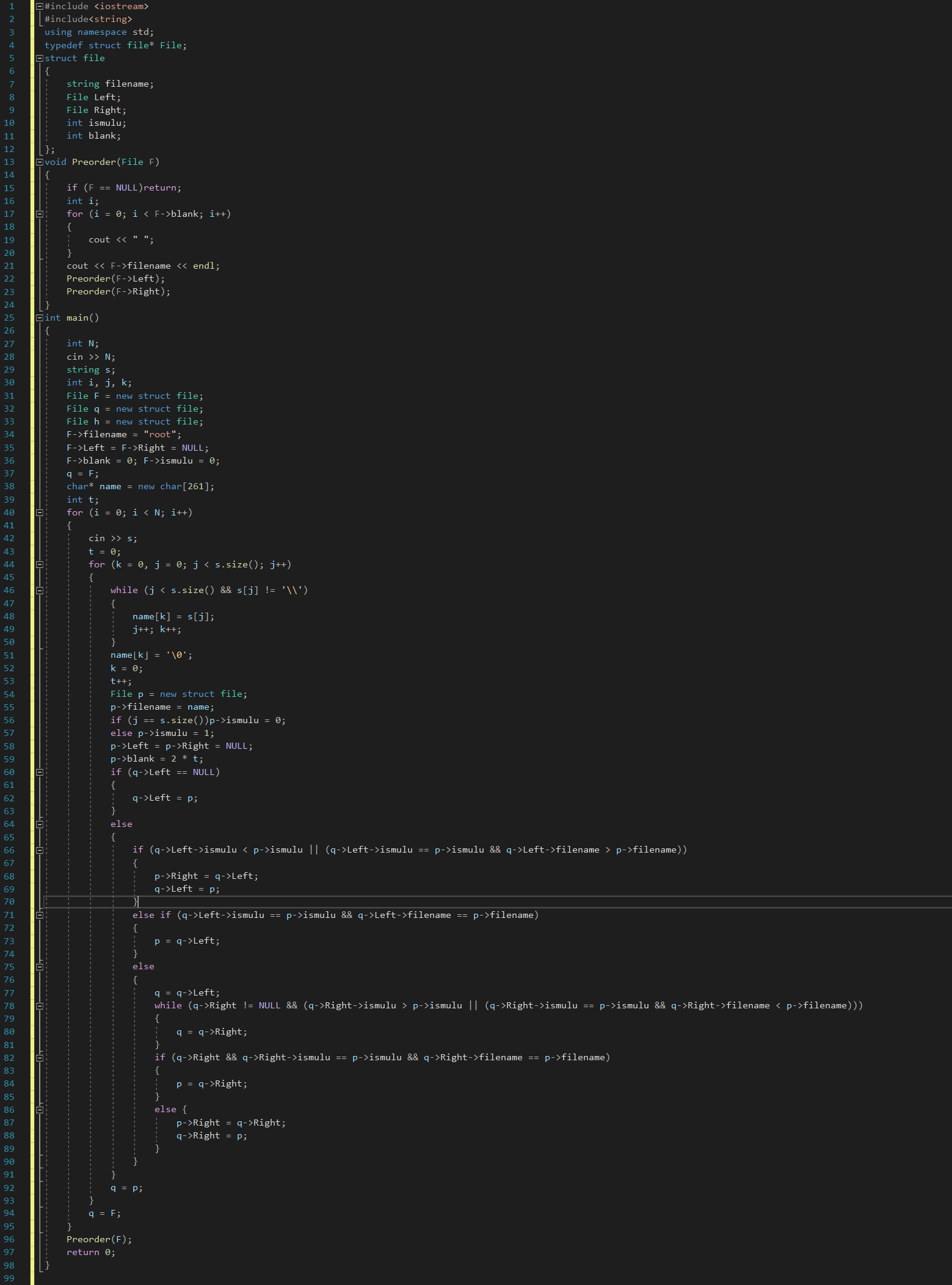
2.2.1 解题思路及伪代码
首先要注意的是目录和文件输出的优先级不同,优先输出目录,其次是文件。后面跟了\的就是目录,没有\的是文件。我用结构体中的ismulu区分目录和文件:ismulu=1表示目录,ismulu=0表示文件。
样例中每一层可能有多个结点,属于多叉树,这里通过父子-兄弟表示法,将多叉树转化为二叉树进行表示。父子关系用结点-左孩子表示,兄弟关系用结点-右孩子表示。于是样例转化为二叉树表示如下:
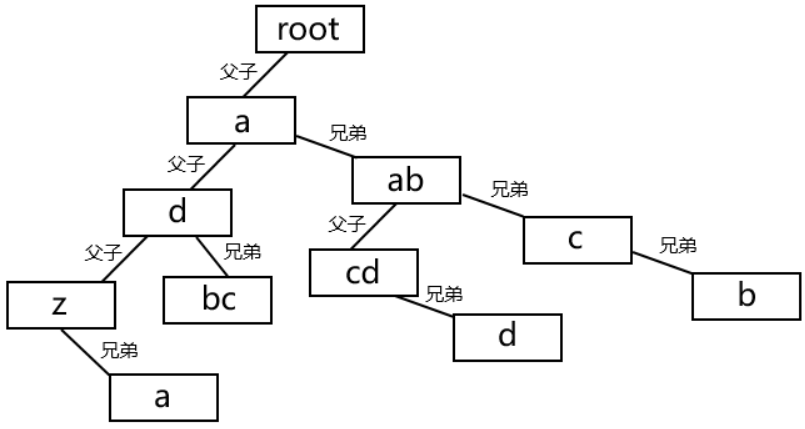
每次读入一行,每一行里面,后一层结点总是作为前一层结点的左孩子(或左孩子的右孩子序列中的结点)插入。因此每一行的内层循环中总是要把q更新为前一层结点。
而读入不同行时,每一次都要将q重新置为根结点F,从根结点开始插入。
最后先序遍历输出各结点和相应的空格数。
2.2.2 总结解题所用的知识点
树的按情况输出和结点插入和先序遍历
多叉树转换为二叉树
3.阅读代码
3.1 题目及解题代码
题目
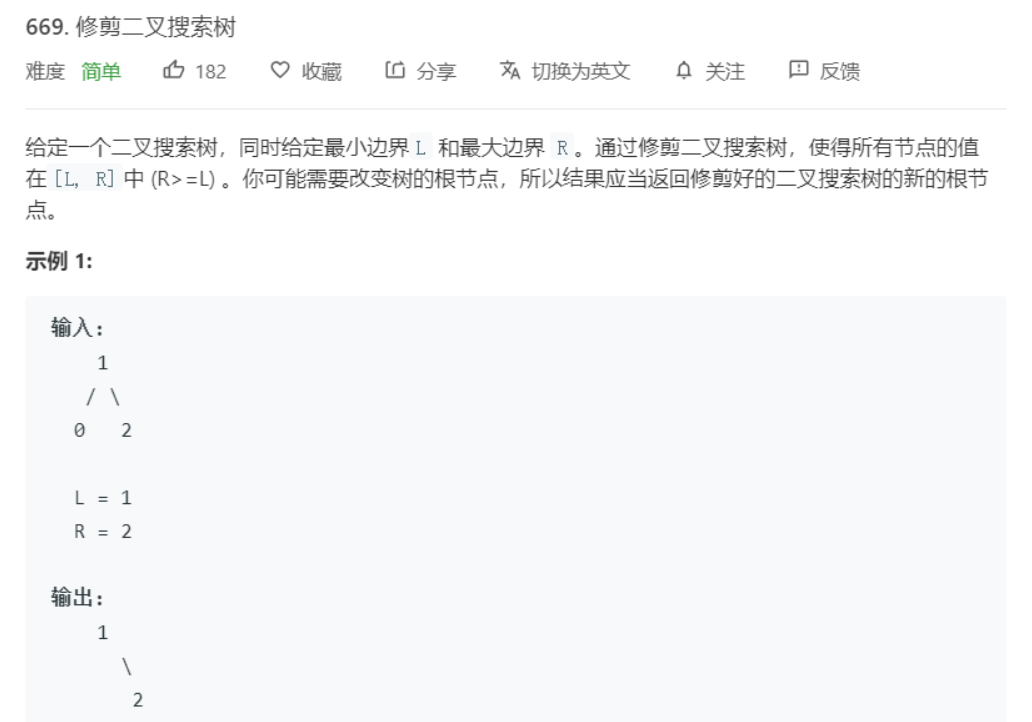
代码

3.2 该题的设计思路及伪代码
设计思路
当 root.val > R,那么修剪后的二叉树会出现在节点的左边。当root.val < L时,那么修剪后的二叉树会出现在节点的右边。否则,修剪树的两边。
时间复杂度:O(N)。
空间复杂度:O(N)。
伪代码
struct TreeNode* trimBST(struct TreeNode* root, int L, int R){
root为空时,返回NULL
若root->val < L
返回trimBST(root->right, L, R);
若R < root->val
返回trimBST(root->left, L, R);
接着找左孩子root->left = trimBST(root->left, L, R);
接着找右孩子root->right = trimBST(root->right, L, R);
}
3.3 分析该题目解题优势及难点
优势:利用递归的算法,减少了代码量,复杂度也相对较小。
难点:修减时如何替代前一个结点。




