【读书笔记】信息论专题总结——特定信源分布的率失真函数计算

之前在学信息论这门课的时候，对于求率失真的方法虽然记住了，但是并没有理解。这次重新梳理率失真的计算方法，并对重点问题的思考做一个记录。本轮梳理将以Cover & Thomas的EoIT教材作为主要大纲，并结合一些参考文献：

• 特定信源分布下的率失真函数计算

  • 单个离散信源-伯努利分布

  • 单个连续信源-正态分布、拉普拉斯分布

• 向量信源的率失真函数计算

• 计算率失真函数的一般方法：Blahut-Arimoto算法

之后可能会再对率失真的建立等问题进行专题梳理，不过由于时间限制，本篇博客将仅专注于特定信源分布下率失真函数计算这一个方面。

本文的总体思路如下：

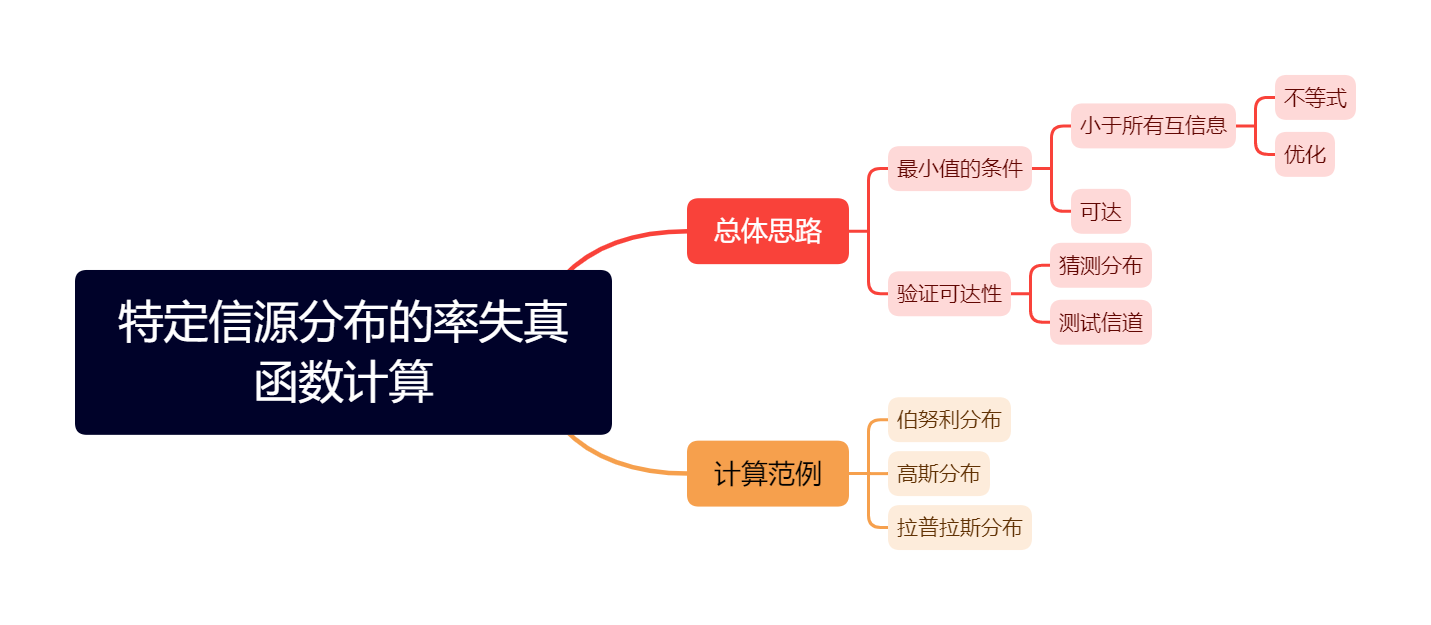
总体思路

率失真函数的定义就是给定失真度量下互信息的最小值，即\(R(D)=\min_{\mathbb E [d]\le D} I(X;\hat X)\)。至于为什么率失真就是约束条件下的互信息最小值，这是由其他可达性、逆定理确定的，在计算率失真函数时可以不考虑。总之，我们的目标就是计算互信息的最小值。

要达到这个最小值，所求函数需要满足两个条件：

1. 在可行域内所有的互信息都比这个函数大

2. 这个函数是可达的

对应的证明思路如下：

互信息的最小值

第一种方法是用优化的思路直接求解，这是一种通用方法，因此不过多说明。另一个方法则是用若干不等式得到互信息的下界，然后根据所用条件的多少来判定这个值是率失真函数的上界还是下界。实际操作中，也可以两个方法混用，比如先用不等式简洁地得到某个下界，然后再对这个下界进一步用优化方法求解最小值。

在在逻辑上，第二种方法相当于利用所有已知条件和约束条件，不断的扩展可达区域。从而得到“在题目假设条件下，互信息一定大于等于某一个值”的论断。这显然是更有信息论意味的方法，也是在已知信源特定分布下，更简洁的求解方法。

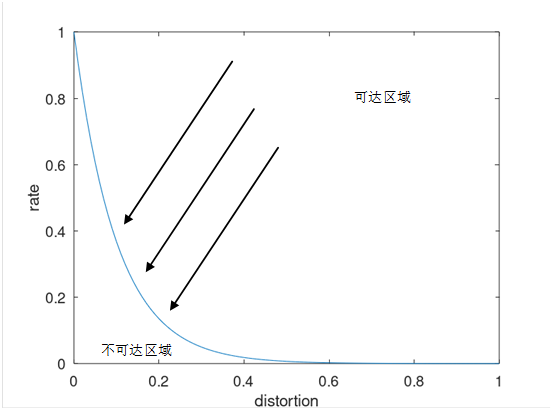
在具体推导时，还有如下两点值得说明：

1. 如何将失真约束体现在互信息中？

   根据互信息的定义，常用的计算表达式为

   \[I(X ; \hat{X})=H(X)-H(X \mid \hat{X}) \]

   这是因为信源的分布是已知的，因此只需要处理后一个条件熵。对于条件熵而言，就要想办法转化成失真的度量形式，以此将失真要求\(D\)体现在互信息的下界中。

2. 如何选取合适的不等式？

   • 首先是对界“紧”的要求。一方面，我们要尽可能用强有力的不等式，能够把互信息的下界逼得足够小，而不是用一个不等式就停止了。同时，我们也希望推导出的界是可达的，从而避免过度放松导致推导的界没有意义。

   • 另一个方面是“可解”。利用不等式不仅是为了推导出最小值，更是为了得到一个便于计算的解。

可达的互信息

在验证可达性上，通常都是看不等式推导中，如果要取等会用到哪些条件，然后构造相应的转移概率来满足这些条件。当有了这个概率过后，自然就可以得到联合概率。因此也可以说，不管是考虑原始信源到压缩信源的转移概率，还是压缩信源到原始信源，只要满足原始信源的分布条件即可。这就为测试信道的建立提供了保障。当然，测试信道只是当直接求转移概率不方便时候的一种技巧，并不是说就一定的从测试信道入手进行分析。

上下界

对于特定分布信源的压缩问题，这两个条件能够同时满足，也就得到了准确的率失真函数。但实际计算的话，如果没有那么好的结果，就只能得到真实率失真函数的上下界。

• 上界：只能证明所求函数是可达的，并不能说明可行域内所有互信息都比该函数大

  这种场景来自于我们难以求得具体的率失真函数表达式，因此需要加一些条件，使得先满足可达性，再对这个上界利用不等式或者优化方法进行最小化。这个思路可以参照语义通信小组文档《wanli-对一个率失真小模型的一些讨论-221114》中求上界的部分。

• 下界：一个足够小的互信息，但是无法构造出一个转移分布来证明这个函数是可达的

  求下界的原因在于，有些题设条件不好用，因此暂且不用。此时可行域变大，所得最小值很有可能小于真实的率函数。换言之，率失真函数不可能比这个函数还要小。

备注：加减条件对于优化问题的上下界影响：

• 加条件，可行域变小，最值不最，最小值成上界，最大值成下界

• 减条件，可行域变大，最值更最，最小值成下界，最大值成上界

加不见更？ 另外需要说明的是，这些条件并不包含不等式成立的一般条件，因为这些条件是提前早已假设的（诸如条件熵不等式，其条件是普遍满足的）。

其他

具体推导过程中哪些不等式是常用的，为什么要用这些不等式，在对单个信源都进行分析后再进行总结。

现在假设我们已经得到了不等式，接下来就需要通过构造可达的分布来验证其是否是最小值。由于互信息一定非负，因此对于取零点时的失真值也要单独列举出来。这个是技巧性更强的步骤，之后也单独总结。

特定信源率失真函数的关键问题回答

伯努利信源

• 如何比较跳转概率\(p\)和失真度量\(D\)的关系？

  从\(I(X;\hat{X})\ge H(p)-H(D)\)的非负性上得到启发，\(p\)和\(D\)的相互大小关系应该会影响最终结果。其实就是如果直接摆烂，在压缩端始终取某一定值，是否能够满足失真约束。若能满足的话，直接就有\(R(D)=0\)了。

高斯信源

• 以下计算式为什么不正确？

\[\begin{align} h(X|\hat{X}) &= h(X-\hat{X}|\hat{X}) \\ &= \int h(X-\hat{X}|\hat{X}=a)p(a)da \\ &= \int h(X)p(a)da \\ &= h(X) \end{align} \]

计算过程中的条件带掉了。

实际应该有

\[\begin{align} h(X-\hat{X}|\hat{X}=a) &= h(X-a|\hat{X}=a) \\ &= h(X|\hat{X}=a) \\ &\neq h(X) \end{align} \]

拉普拉斯信源

如何构造参考分布\(Q\)？目前尚未找到足够多的规律。