【课程笔记】中科大信息论(五)
相对熵
注意是对放在前面的\(p(x)\)取期望
相对熵的非负性
-
用IT不等式进行证明
-
是一个很有用的性质(感觉和IT不等式差不多)
-
证明均匀分布有最大熵
\[\begin{aligned} 0 \leq D\left(p \| p_{\mathrm{u}}\right) &=\sum_{x \in X} p(x) \ln \frac{p(x)}{p_{\mathrm{u}}(x)}\\ &=\sum_{x \in X} p(x) \ln (|X| p(x)) \\ \ &=-H(X)+\ln |X| . \end{aligned} \]相对熵哪个分布放前面主要是一种经验
更多时候是根据某种性质找到了这个分布
均匀分布:分布是一个常数
几何分布:分布取对数后有X
-
证明给定均值时,几何分布有最大熵
(感觉这种证明都是先找到了或者构造或者猜一个分布,然后确实ok,没有什么固定套路)
\[\begin{aligned} 0 \leq D\left(p \| p_{\mathrm{g}}\right) &=\sum_{x=1}^{\infty} p(x) \ln \frac{p(x)}{p_{\mathrm{g}}(x)} \\ &=-H(X)-\sum_{x=1}^{\infty} p(x) \ln p_{\mathrm{g}}(x) \\ &=-H(X)+\ln A+(E X-1) \ln \frac{A}{A-1} \\ &=-H(X)+A \ln A-(A-1) \ln (A-1) \\ &=-H(X)+H\left(X_{\mathrm{g}}\right) . \end{aligned} \]为什么\(\{1,2,...,2A-1\}\)上的均匀分布不满足?
对于任意的\(p(x)\)而言,当\(p_g(x)=0\)的时候,\(p(x)\ln 0\)没法计算了
-
应用:a guessing problem
Suppose that we want to guess the value of a discrete R.V. X; that is, we repeatedly declare our guessed value of X, until the guessed value coincides with the true value.
How many guesses do we need, on average?猜测次数的概率意义是什么,是分布的均值;
X的分布未知,如何能联系上均值?
那么不妨先给定一个均值A,不管分布怎么变,分布的熵会小于对应几何分布的最大熵,而这个最大熵刚好仅仅和A有关,是A的函数
所以得到了均值的关系
\[H(X) \leq H\left(X_{g}\right)=A \ln A-(A-1) \ln (A-1)\le \ln A -1 \]最终有\(H(X) \leq \ln A+1 \text {, i.e., } E[X] \geq e^{H(X)-1}\)
-
-
互信息
联合分布与边缘分布的相对熵
信息密度比互信息能提供更加全面的\(X\)和\(Y\)关系的刻画
互信息和熵的关系
- 自信息就是熵:\(I(X ; X)=H(X)\)
- 凹凸性:
- $(X;Y ) $ is a convex function with respect to \(p(y|x)\), for any fixed \(p(x)\)
- and is a concave function with respect to \(p(x)\), for any fixed \(p(y|x)\)
条件互信息
只要不是小写,取期望的时候都是\(P(x,y,z)\)的联合概率
条件熵会减小,但是条件互信息没有这个性质
互信息的链式法则
-
证明:
先写成两个熵相减,然后用熵的链式法则展开,再对应相减还原成互信息
![image-20220408100232701]()
-
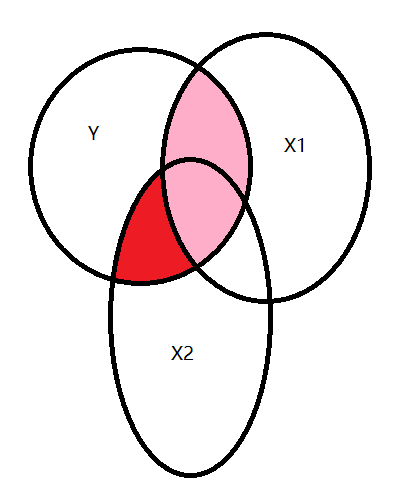
理解:
所有\(X_i\)和\(Y\)的互信息相加,但要减去之前加过的互信息,因此作为条件
![image-20220408100632897]()


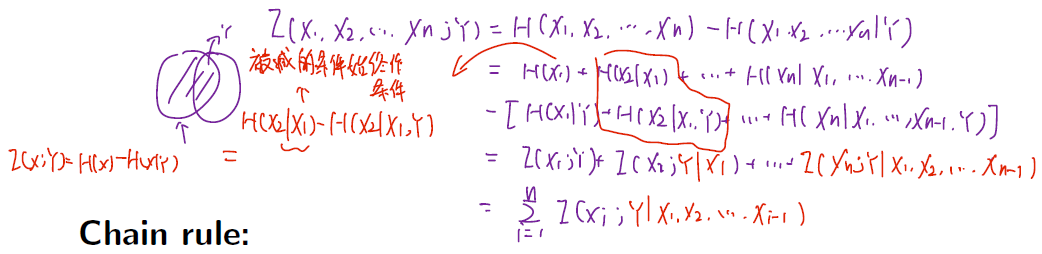

 浙公网安备 33010602011771号
浙公网安备 33010602011771号