【课程笔记】中科大计算经济学（三）

秘书问题

假设有三个秘书轮流面试，需要当场决策，如何找到最合适的秘书？

最优策略

• 先看第一个，不选
• 看第二个
  • 如果比第一个好，选第二个
  • 如果没有第一个好，选第三个

分析

如果随机三选一，选到最好秘书的概率是1/3

如果按照最优策略，选到最好秘书的概率是1/2

按照条件概率进行计算：

\[\frac{1}{3}\times 0+\frac{1}{3}\times 1+\frac{1}{3}\times\left(\frac{1}{2}\times 0+\frac{1}{2}\times 1\right)=\frac{1}{2} \]

Shapley value

含义

衡量有你和没你的差距

适用于只能抽取集体、不能抽取个体时，通过子集的贡献来反推个人的贡献

难点

• 组合太多无法计算
• 如何计时得到value

博弈论初步

基本元素

• 理性地play时玩家间的公共知识

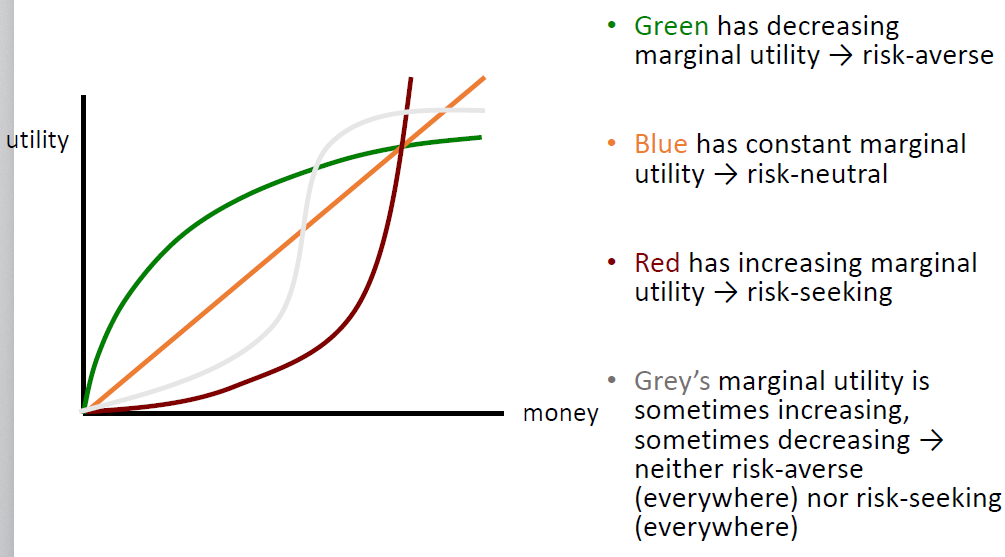
• 考虑到用户对风险的偏好程度，utility不等于value

  

表示方法

• normal form：适用于simultaneous-move下的博弈

  • 基本要素

    

  • 其他要素：type

    • 个体的独有信息（如估价）
    • 效用与输出的关系\(u_i=g_i(S_i,t_i)\)
      • utility同时收到action（出价多少）和type（估价多少）的影响
      • 一般情况下是线性函数
      • 常见形式为\(u_i=-P_i+t_i\)，即付出的钱加上估价

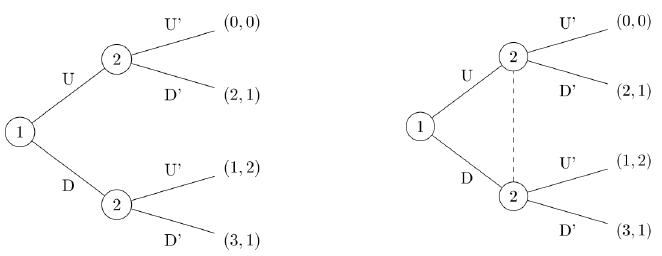
• extensive form：树状图

  

  • 每一层表示一个人或者一个state

  • 虚线表示不知道该节点之前的状态，如果全是实线则表示知道所有用户的所有信息（perfect information）

Braess paradox

问题描述：路由问题

原始情况，所有用户路程综合为1.5

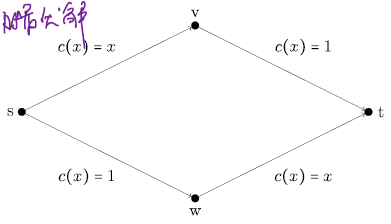
添加一条捷径后时间总和反而增加为2（NE）

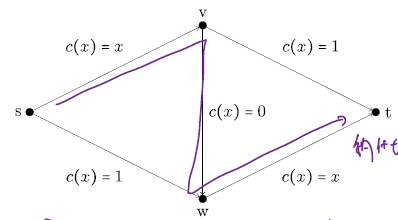
大家都会走同一条路

结论

• 修路过后更堵了

• 计算PoA无序代价

  \[\frac{NE}{Opt}=\frac{2}{3/2}=\frac{4}{3} \]

  接近于1，意味着即使花了时间协调，也不会带来太大的效果