【课程笔记】中科大信息论（四）
熵率
为什么要研究熵率
除了研究i.i.d.随机变量的熵，之前已经从条件熵的角度研究了两个关联的随机变量之间的关系，现在想进一步研究当这些随机变量来自于某个随机过程时的情况。我们已知随着随机变量数目的增加，其联合熵也会不断增加\(H\left(X_{1}, X_{2}, \ldots, X_{n}\right)\le H\left(X_{1}, X_{2}, \ldots, X_{n+1}\right)\)，因此再研究增长趋势就没有意义，我们转而考虑整个随机过程地研究熵率
\[H(X)=\lim _{n \rightarrow \infty} \frac{1}{n} H\left(X_{1}, X_{2}, \ldots, X_{n}\right)
\]
（严）平稳过程
在任一时间点后，任意个随机变量的联合分布都没有发生改变
- 宽平稳只保证一二阶矩不改变
- 高斯过程的宽平稳与严平稳等价
马尔可夫过程
- 信息论中一般考虑三个变量间的关系，再长就是长Markov链的研究范围了
时不变马尔可夫链
-
条件概率只与随机变量取值有关，与状态下标无关
-
时不变马尔可夫链+稳态分布→平稳随机过程
-
稳态分布：\(X_n\)的分布与\(X_{n+1}\)分布相同（每一个状态的出现概率不再变化）
-
稳态分布的计算：\(\underline{p}=\mathrm{P} \underline{p}\)（注意还有一个概率和为1的条件）
-
证明：
-
平稳马尔可夫链的熵率
-
平稳过程的熵率存在且等于条件熵的极限
\[H(X)=\lim _{n \rightarrow \infty} \frac{1}{n} H\left(X_{1}, X_{2}, \ldots, X_{n}\right)=\lim _{n \rightarrow \infty} H\left(X_{n} \mid X_{n-1}, \ldots, X_{1}\right) \]-
证明：
-
-
平稳马尔可夫链的熵率：\(H(X)=H\left(X_{2} \mid X_{1}\right)\)
-
给定转移矩阵与稳态分布后，可以进一步得到具体值
-
-
熵率的图像
-
考虑跳转概率分别为\(\alpha\)和\(\beta\)的两状态马尔科夫链
-
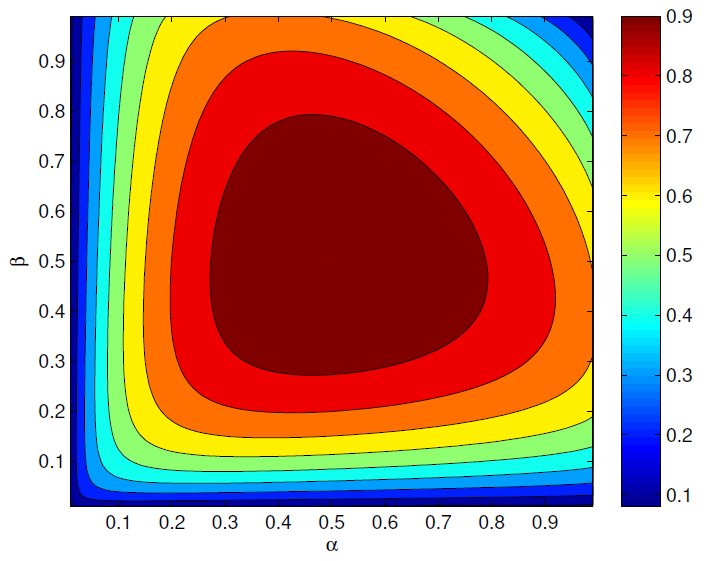
contour plot
- 含义是在这个马尔科夫链的随机过程中，平均每个状态的熵是多少
- 如果跳转可能比较固定（跳或者不跳的概率高），熵比较少，也就是说比较稳定
- 如果频繁发生跳转，捉摸不定，熵大，不确定度大，信息量大
-
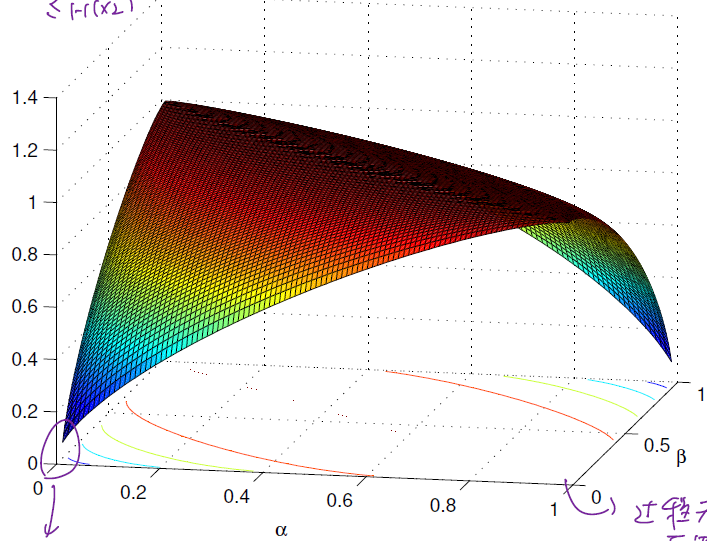
比值图像
- 含义是在马尔科夫链中，熵率相对于稳态分布的熵小了多少，也就条件带来的信息量有多少
- 同样在跳转情况比较固定的时候，条件带来的不确定的消减很大（较小的部分）
- 在跳转比较随机的时候，历史记录没什么关系（趋近1的部分）
-
