贪心杂题
有关一些贪心题目
基本由易到难吧
Simple Game
https://www.luogu.com.cn/problem/CF570B
很容易可以推出来,具体概率算法是几何概型似乎:
2*m<=n的时候,答案为m+1;
2*m>n的时候,答案为m-1;
特殊情况,若m=1,答案就为1。
国王游戏
https://www.luogu.com.cn/problem/P1080
贪心策略:按左右手乘积从小到大排序
证明方法,从队列中选两个相邻的交换位置,可证明出乘积小的在前面更优
具体就不详写了,证明很容易
这道题除贪心外的点在于要用高精度,高精度乘法与除法
高精度的话vector还挺好用的
附上代码:

#include<bits/stdc++.h> using namespace std; pair<int,int> st[10005]; vector<int> mul(vector<int> a,int b) { vector<int> c; int t=0; for(int i=0;i<a.size();i++) { t+=a[i]*b; c.push_back(t%10); t/=10; } while(t) c.push_back(t%10),t/=10; return c; } vector<int> div(vector<int> a,int b) { vector<int> c; int t=0; bool zr=0; for(int i=a.size()-1;i>=0;i--) { t=t*10+a[i]; int x=t/b; if(x||zr) zr=1,c.push_back(x); t=t%b; } return vector<int>(c.rbegin(),c.rend()); } vector<int> Max(vector<int> a,vector<int> b) { if(a.size()>b.size()) return a; if(a.size()<b.size()) return b; for(int i=a.size()-1;i>=0;i--) { if(a[i]>b[i]) return a; else return b; } return a; } void output(vector<int> a) { for(int i=a.size()-1;i>=0;i--) printf("%d",a[i]); printf("\n"); } int main() { int n; scanf("%d",&n); for(int i=0;i<=n;i++) { int x,y; scanf("%d%d",&x,&y); st[i]={x*y,y}; } sort(st+1,st+n+1); vector<int> now(1,1); vector<int> ans(1,0); for(int i=0;i<=n;i++) { if(i) ans=Max(ans,div(now,st[i].second)); now=mul(now,st[i].first/st[i].second); } output(ans); return 0; }
Radar Installation
http://poj.org/problem?id=1328
对于任意一个点(x,y),所能把它监控到的雷达范围在(x1,x2)间
x1=x-sqrt(R*R-y*y),x2=x+sqrt(R*R-y*y)

于是问题转化为了在一些区间内找到最少的点,使每个区间至少有一个点在范围内
对于上述问题,贪心策略为:按照对每个区间按右端点从小到大排序,每次需要取新的点时取在右端点上
每次更新新点的条件为:当前区间的左端点比当前点大,则取新点在当前区间的右端点上
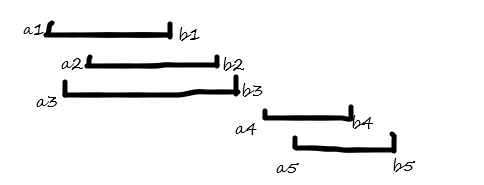
如图:第一个点取在b1上,则当前点now=b1,已取的点个数ans=1
a2<now,无需更新,跳过,同理跳过第三个区间
到第四个区间,a4>now,则更新新点now=b4,ans++
同理判断第五个区间,得到最终答案ans=2
此时的ans即为在所有区间的找到最少点的答案,也即为此题的答案
代码简单就不附上了
color a tree
http://poj.org/problem?id=2054
题意是有一棵树,要对它的每个节点染色,每次染色付出的代价是这个点的权值乘以它染色的次序(第几个染),求最小代价和
限制条件是给当前点要能染色,它的父节点必须已经染色
首先,对于一些点来说,如果没有限制条件,则很容易想到贪心策略:
按权值大小排序,先染大的点
有了限制条件后,找到最大的点后,不能直接把它染色,要先保证它的父节点已染色
所以,虽然不知道当前最大的点什么时候染色,但把它排在它的父节点后一定是最优的
即,当前最大点与它的父节点一定是顺序紧挨着
此时,就可以把这两个点看成一个整体,将最大点合并到它的父节点去
对于这样的一个整体,与一个单个的点比较:设整体为父节点a1,子节点a2,单个点为b
若a1,a2在b前面,则代价c1为:a1+2*a2+3*b
若b在a1,a2前面,则代价c2为:b+2*a1+3*a2
c1-c2=2*b-a1-a2
若c1>c2,即b>(a1+a2)/2;反之,若c1<c2,即b<(a1+a2)/2
也即,如果b大于整体均值,则将b放在整体前更优,反之亦然
再对于两个整体,同理易证,将均值放在前面更优
此时,就可以得到整道题的贪心策略:
从除根节点外的所有点中找出最大的一个,合并入它的父节点,将父节点权值更新为两点的均值,删除原点,整体相当于一个新的点
重复直至所有点合并到根节点
但是,对于答案的统计,合并完后再挨个叠加,并不容易
所以,在每次合并时,统计答案
对于,一个整体x与一个整体y,假设将y合并到x去,付出的代价就应为,y中每个点的权值*x中的点数
相当于把y排在x的后面,那么y中每个点就都往后排了x中点个数个位置,需付出的代价就是y中每个点的权值乘以x中点个数
附上代码

#include<iostream> using namespace std; int n,root; struct jsy { int w,size,father; double avg; }tree[1005]; int find() { double maxx=0; int v=-1; for(int i=1;i<=n;i++) { if(i!=root&&tree[i].avg>maxx) { maxx=tree[i].avg; v=i; } } return v; } int main() { while(1) { int ans=0; cin>>n>>root; if(n==0&&root==0) break; for(int i=1;i<=n;i++) { cin>>tree[i].w; tree[i].size=1; tree[i].avg=tree[i].w; ans+=tree[i].w; } for(int i=1;i<n;i++) { int x,y; cin>>x>>y; tree[y].father=x; } for(int l=1;l<n;l++) { int ver=find(); int f=tree[ver].father; ans+=tree[ver].w*tree[f].size; tree[ver].avg=-1; for(int j=1;j<=n;j++) { if(tree[j].father==ver) tree[j].father=f; } tree[f].size+=tree[ver].size; tree[f].w+=tree[ver].w; tree[f].avg=(double)tree[f].w/tree[f].size; } cout<<ans<<endl; } return 0; }
好久没有写博客了
这两周做的贪心题就这几道,还有几道真的非常简单的题就没放了
暂时先写几道,会持续更新


