堆

堆

堆的应用比较多，比如堆排序等等，下面就来介绍下堆

堆是一棵树（完全二叉树）的形式，其每个结点都有一个值，且每个结点的值都大于/小于等于其父结点的值

• 小根堆：每个结点的值都大于等于其父结点的值
• 大根堆：每个结点的值都小于等于其父结点的值

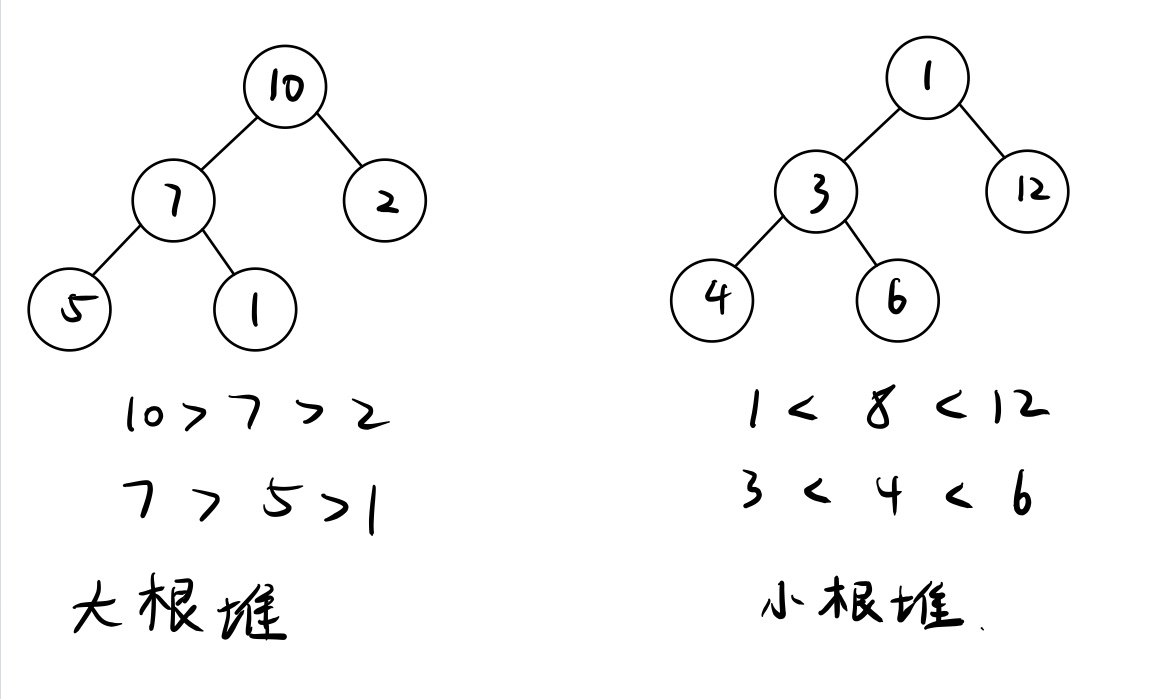
注意：堆的根结点存放的是最大值或者最小值，但其他结点的值的排序是未知的，这与二叉搜索树不同

堆的基本操作

• 插入一个数

  在末尾插入新的元素，然后向上调整

• 求堆中的最小(大)值

  返回堆顶元素

• 删除最小值

  用末尾的元素去覆盖堆顶元素，然后再将堆顶元素向下调整

• 删除任意一个元素

  将任意一个元素覆盖堆顶元素，然后再将堆顶元素向下或者向上调整

• 修改任意一个元素

  直接赋值，再将该元素向上或者向下调整

const int N = 100010;
int heap[N],l;

void down(int x) {
  //用t来代表根结点和其左右儿子中的最小值的下标
  int t = x;
  //如果左儿子存在且左儿子小于t，则t等于左儿子
  if (x * 2 <= l && heap[x * 2] < heap[t]) {
   	 t = x * 2; 
  }
  if (x * 2 + 1 <= l && heap[x * 2 + 1] < heap[t]) {
    t = x * 2 + 1;
  }
  //当根结点不是最小值的时候
  if (x != t) {
    swap(heap[t],heap[x]);
    down(t);
  }
}

void up(int x) {
  //当该点有父结点且该点的值大于其父结点的值，则进行交换
  while (x/2 > 0 && heap[x/2] > h[x]) {
    swap(heap[x/2],heap[x]);
    x /= 2;
  }
}

//最小值
heap[1];

//删除最小元素
heap[1] = heap[l];
l--;
down(1);

解释：为何删除元素时需要覆盖堆顶元素，再调整

由于我们使用数组储存堆，在数组中，删除第一个元素比较困难，但删除最后一个元素比较简单，我们只需要用最后一个元素覆盖掉第一个元素，这样一来，最后一个元素还保存在数组中，只是位置变了，而要删除的元素已经不在了，此时我们使数组的长度减一，再将第一个元素进行排序，调整到合适的位置即可

堆的储存方式

我们采用数组的方式去实现堆

下标从1开始时：

• x的左儿子：2 * x
• x的右儿子：2 * x + 1

堆的建立

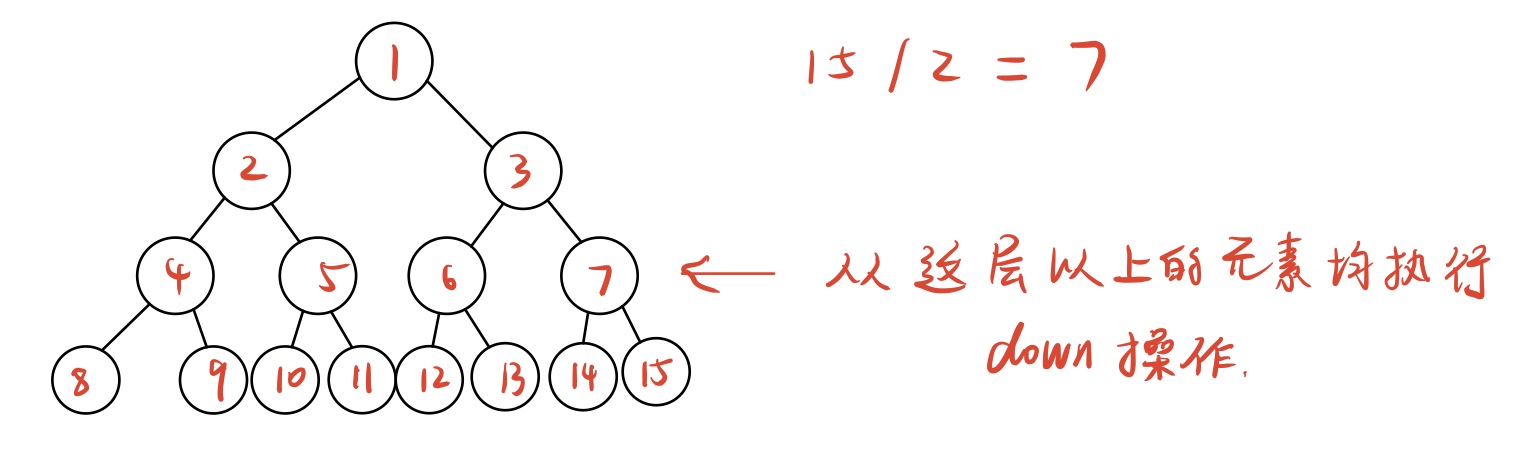
我们在数组储存了所有的元素后，需要建堆，此时我们一般采用一种O(n)的方法来实现

以小根堆为例，我们从n/2处的元素开始执行向下调整(down)操作

for (int i = n/2;i > 0; i--) {
  down(i);
}

解释：因为n/2是堆的倒数第二层，所以我们将上面的所有元素都进行一个下沉操作来维护堆的有序

STL中的堆

c++中，提供了一个优先队列，实现堆的功能

priority_queue自动实现排序

//大根堆
priority_queue<int> heap;
//小根堆
priority_queue<int,vector<int>,greater<int>> heap;

//返回堆顶元素
heap.top();
//向堆插入一个数
heap.push(1);
//弹出堆顶元素
heap.pop();
//判断堆是否为空
heap.empty();
//返回元素个数
heap.size();