hdu4746莫比乌斯反演进阶题

Mophues

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 327670/327670 K (Java/Others)
Total Submission(s): 1922    Accepted Submission(s): 791

Problem Description

As we know, any positive integer C ( C >= 2 ) can be written as the multiply of some prime numbers:
    C = p1×p2× p3× ... × pk
which p1, p2 ... pk are all prime numbers.For example, if C = 24, then:
    24 = 2 × 2 × 2 × 3
    here, p1 = p2 = p3 = 2, p4 = 3, k = 4

Given two integers P and C. if k<=P( k is the number of C's prime factors), we call C a lucky number of P.

Now, XXX needs to count the number of pairs (a, b), which 1<=a<=n , 1<=b<=m, and gcd(a,b) is a lucky number of a given P ( "gcd" means "greatest common divisor").

Please note that we define 1 as lucky number of any non-negative integers because 1 has no prime factor.

 

 

Input

The first line of input is an integer Q meaning that there are Q test cases.
Then Q lines follow, each line is a test case and each test case contains three non-negative numbers: n, m and P (n, m, P <= 5×10⁵. Q <=5000).

 

 

Output

For each test case, print the number of pairs (a, b), which 1<=a<=n , 1<=b<=m, and gcd(a,b) is a lucky number of P.

 

 

Sample Input

2

10 10 0

10 10 1

 

 

Sample Output

63

93

 

http://blog.csdn.net/wh2124335/article/details/11846661 转载自此

 

记录一下自己的思路

未简化过的代码核心应该是这样的

 

   for(int i=1;i<=n;++i)//枚举每个因子  
   if(d[i]<=k)//如果因子的素数质因子小于等于k
    for(int j=i;j<=n;j+=i) ans+=u(j/i)*(n/i)*(m/i)//枚举F(i);

 

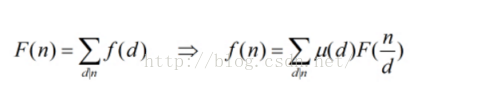
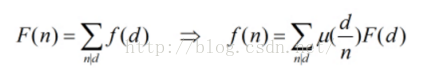
利用的是第二个，然后可以发现，对于每个数字i,他的倍数j的系数都要加上u[j/i],可以与处理出来U(N)，其中U(i)就是u[i/第一个因子]+u[i/第二个因子]+....（这里的U先不考虑素因子个数限制）

那么上述式子就可以化简成为

for(int i=1;i<=n;++i) ans+=U(i)*(n/i)*(m/i);//直接枚举

然后U(i)考虑素因子个数限制的话，那么显然预处理也是可以搞出来的，详细见代码，代码里的cnt[N][19]就是U考虑限制的。

然后就是普通的分块操作，为了简化时间，因为W=(n/i)*(m/i)，i倘若在一定范围内，这个W是不变的，所以可以加速。

 

所以最后就是这样了

for(int i=1,last=i;i<=n;i=last+1){
            last=min(n/(n/i),m/(m/i));
            ans+=(ll)(cnt[last][k]-cnt[i-1][k])*(n/i)*(m/i);
        }

 

#include<cstdio>
#include<cstring>
#include<iostream>
#include<vector>
using namespace std;
const int maxn = 500100;
typedef long long ll;
int mu[maxn],sum[maxn],num[maxn];
ll cnt[maxn][19];
bool flag[maxn];
vector<int>prime;
void init(){
    mu[1]=1;
    for(int i=2;i<maxn;i++){
        if(!flag[i]){
            prime.push_back(i);
            mu[i]=-1;
            num[i]=1;
        }
        for(int j=0;j<prime.size()&&i*prime[j]<maxn;j++){
            flag[i*prime[j]]=true;
            num[i*prime[j]]=num[i]+1;
            if(i%prime[j])mu[i*prime[j]]=-mu[i];
            else {mu[i*prime[j]]=0;break;}
        }
    }
    for(int i=1;i<maxn;i++){
        for(int j=i;j<maxn;j+=i){
            cnt[j][num[i]]+=mu[j/i];
        }
    }
    for(int i=0;i<maxn;i++){
        for(int j=1;j<19;j++){
            cnt[i][j]+=cnt[i][j-1];
        }
    }
    for(int i=1;i<maxn;i++){
        for(int j=0;j<19;j++){
            cnt[i][j]+=cnt[i-1][j];
        }
    }
}
int main(){
    init();
    int q;
    scanf("%d",&q);
    while(q--){
        int n,m,k;
        scanf("%d%d%d",&n,&m,&k);
        k=min(k,18);
        ll ans=0;
        if(n>m)swap(n,m);
        for(int i=1,last=i;i<=n;i=last+1){
            last=min(n/(n/i),m/(m/i));
            ans+=(ll)(cnt[last][k]-cnt[i-1][k])*(n/i)*(m/i);
        }
        //printf("%lld\n",ans);
        printf("%I64d\n",ans);
    }
}