1 CH算法的基本原理
CH(Contraction Hierarchies)算法是 Robert Geisberger、Peter Sanders、Dominik Schultes及Daniel Delling于2008年发布的，它是一种用于查找图形中最短路径的加速技术。最直观的应用是汽车导航系统：用户希望使用最快的路线从A行驶到B。此处优化的指标是行驶时间。交叉路口由顶点表示，街道路段由边连接。边的权重代表沿着这条街道行驶所需的时间。从A到B的路径是一系列边（街道）；最短的路径是所有可能路径中边的权重总和最小的路径。
graph中的最短路径可以使用Dijkstra算法来计算，但考虑到道路网络包含数千万个顶点，这是不切实际的。CH算法是一种优化的加速方法，可以利用代表道路网络的图的特性。通过在预处理阶段创建“shortcuts”来实现提速，然后在最短路径查询中使用这些“shortcuts”来跳过“不重要的”顶点。这是基于对道路网络高度分层的观察。与一些通向小区内部路的路口相比，某些路口（例如高速公路路口）在层次结构中“更重要”并且在层次上更高。“shortcuts”可用于保存两个重要路口之间预先计算的距离，从而算法无需在查询时考虑这些路口之间的完整路径。CH不知道人类认为哪条道路“很重要”，但是它能够使用启发式方法计算出顶点的重要性。
CH方法不仅应用于汽车导航系统，而且还应用于Web和移动设备的路线规划、交通模拟和物流优化。有很多开源软件实现了该算法，例如GraphHopper、OSRM及OpenTripPlanner。
CH算法包括路网预处理和查询两个阶段。由于道路网络很少更改，因此可以预先进行一些计算（几秒钟到几小时），然后再进行查询，查询时间可以达到毫秒级。CH算法依靠“shortcuts”来实现这种加速。“shortcuts”线段连接两个不相邻的顶点 u和v，它的边权重是最短u-v路径上边权重的总和。
考虑通过高速公路连接的两个大城市。我们可以预先计算出两个城市之间高速公路的连接路线，将它保存起来。之后每次查询从一个城市到另一城市的路线时，只需要查询到本城市高速出入口的路线即可。这种预先计算的优势称为“shortcuts”，在现实世界中没有实际的路线。CH算法不了解道路类型，但是能够根据输入的图形来确定创建哪些“shortcuts”。
2 关键技术
Shortcuts
CH算法依赖在预处理阶段创建的“shortcuts”来减少搜索空间，即CH查询时必须查看的顶点数，从而提高搜索效率。为达到这个目标，需要执行迭代式的顶点收缩。我们通过一次“收缩”一个节点来预处理图形。为了执行收缩，我们计算出节点之间的每条最短路径，并为其插入“shortcuts”，然后将节点标记为已处理。
这里用一个简单的图形来说明节点收缩前后的状态，如图1所示。为了收缩C，我们插入从A到E以及从A到B的“shortcuts”，因为A-> C-> E和A-> C-> B是最短的路线。 我们不需要插入从B到E的“shortcuts”，因为B-> C-> E不是从B到E的最短路径，B-> D-> E较短。
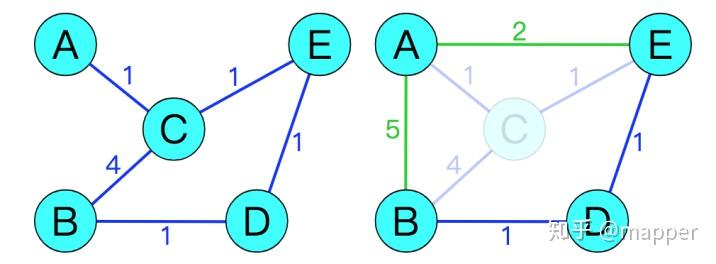图1 node收缩示意图
收缩并不是完全删除节点，但是在其余的收缩过程中可以忽略该节点，因为当我们看到一条通向C的边时，我们知道存在一条捷径，或者它不是一条最短的路径。无论哪种方式，我们都不需要访问C。如果我们进行以C开头或结尾的搜索，我们仍然可以找到它。
节点收缩顺序
无论收缩顺序如何，CH算法都会产生正确的结果，但是搜索效率如何取决于收缩顺序。
主要有两种启发式方法来确定节点的收缩顺序：
1）“自下而上”式。计算上更节省的自下而上的启发式方法决定了以“贪吃”的方式收缩顶点的顺序，这意味着顺序是未知的，而是在前一个收缩完成后选择下一个节点进行收缩。在自下而上的启发式方法中，结合使用多种因素来选择下一个顶点进行收缩。 由于“shortcuts”的数量是决定预处理和查询运行时间的主要因素，因此我们希望使其尽可能小。因此，选择下一个要收缩的节点时最重要的因素是收缩节点时添加的边的净数。
2）“自上而下”式。自上而下的启发式算法会在第一个节点收缩之前预先计算整个节点的顺序，这样可获得更好的结果，但需要更多的预处理时间。该方法认为在许多最短路径中包含的顶点比仅在一些最短路径中包含的顶点更重要。这可以使用嵌套解剖来近似。要计算嵌套的解剖，可以将图递归地分为两部分，然后将它们本身分为两部分，依此类推。
节点收缩排序的基本方法是使用优先级队列，该队列的最小元素包含看起来最有收缩吸引力的节点。这里的优先级是几个指标的线性组合，不同指标的线性系数很重要。通常情况下，我们更喜欢减少边数量的收缩，做一个去除五条边的收缩比仅去除四条边的收缩更好！
node收缩的顺序可以用以下一些指标来确定：
1）边的差分（Edge Difference）
可以说ED是最重要的node收缩条件，它的计算如下：ED = node_degree-number_of_shortcuts
node_degree是连接到节点的边的数量
number_of_shortcuts是在删除节点后必须创建的shortcuts数量
ED值越大越先收缩
2）均匀度（Uniformity）
仅使用ED，会获得相当慢的路径规划。应当以均匀的方式收缩图中所有位置的节点，而不是将收缩节点保持在较小的区域中。
3）收缩成本（Cost of contraction）
收缩的一个耗时部分是前向最短路径搜索，以确定“shortcuts”的必要性。 因此，我们可以将搜索空间大小的总和用作优先项。
3 寻路过程
在查询阶段，从原始图上的起始节点s和目标节点t开始进行双向搜索，并通过预处理阶段创建的“shortcuts”进行扩展。为了找到两个节点之间的最短路径，我们执行两次搜索。一次从起始节点进行搜索，一次从结束节点进行搜索，然后我们看它们在哪里相遇。搜索过程与Djikstra的算法相似，但有一条额外的规则：我们仅搜索收缩顺序比当前节点高的节点。在可视化中，这意味着我们仅搜索向上倾斜的边。
