深度学习面试题06:全连接神经网络正向传播与梯度反向传播
目录
链式法则
逻辑回归的正、反向传播
逻辑回归的正、反向传播案例
全连接神经网络的正、反向传播
全连接神经网络的正、反向传播案例
参考资料
|
链式法则 |
类型一:
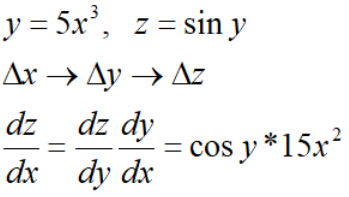
类型二:

类型三:

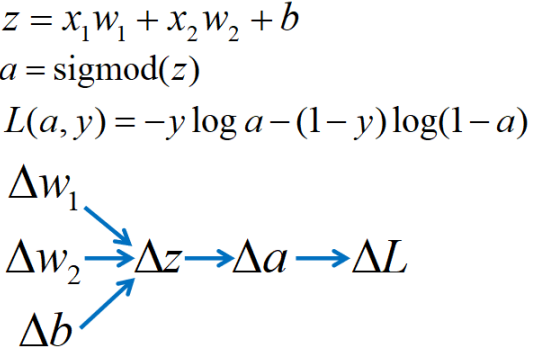
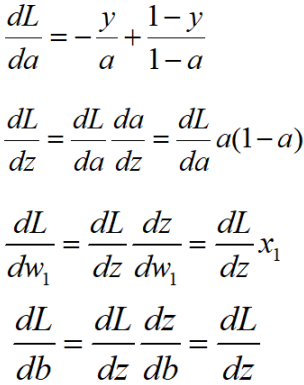
|
逻辑回归的正、反向传播 |
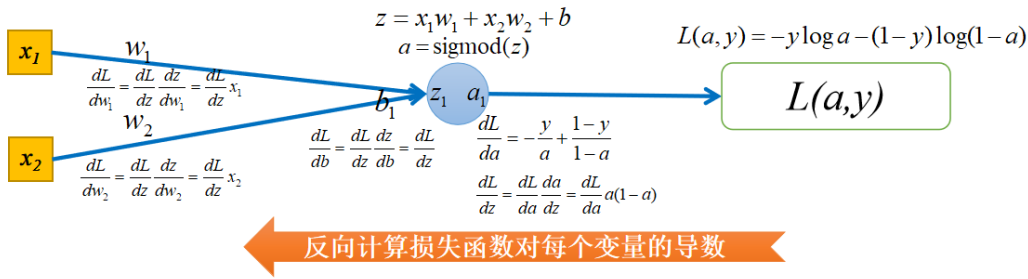
逻辑回归可以看做最简单的神经网络,他只有一个神经元,损失函数选择的是对数损失,他的正向传播过程如下图所示:

逻辑回归可以看做最简单的神经网络,他只有一个神经元,损失函数选择的是对数损失,他的正向传播过程如下图所示:
接下来反向计算损失函数对每个变量的导数。如果你想直接求L对w1的导数是会产生很多重复计算的,回忆下链式求导法则就知道了。因此我们从右向左求导数,这样可以避免重复计算,也就是梯度反向传播的过程,如下图所示:

然后就可以更新w和b,更新模型了,即
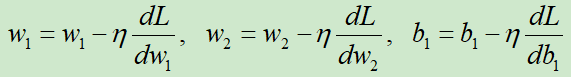
非常简单吧,下面我们通过一个案例演示,看一下如何梯度反向传播(BP算法)是如何降低训练误差的。
|
逻辑回归的正、反向传播案例 |
假设最开始初始化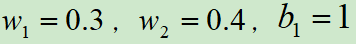 ,本轮训练样本为[(2,3),0],损失函数选用的对数损失,如下图所示:
,本轮训练样本为[(2,3),0],损失函数选用的对数损失,如下图所示:

可以看出在当前模型参数下,正向传播后,损失为2.859
接下来,使用BP算法更新模型参数,如下图所示:

如果再进行正向传播计算损失的话,可以发现,损失从2.859降低到1.682:

|
全连接神经网络的正、反向传播 |
上面举了一个单神经元使用对数损失做分类的例子,这里为了描述全面,阐述一下多神经元做分类的情况,下图是全连接神经网络正向传播的过程:

接下来反向计算损失函数对每个变量的导数。也就是梯度反向传播的过程,如下图所示:
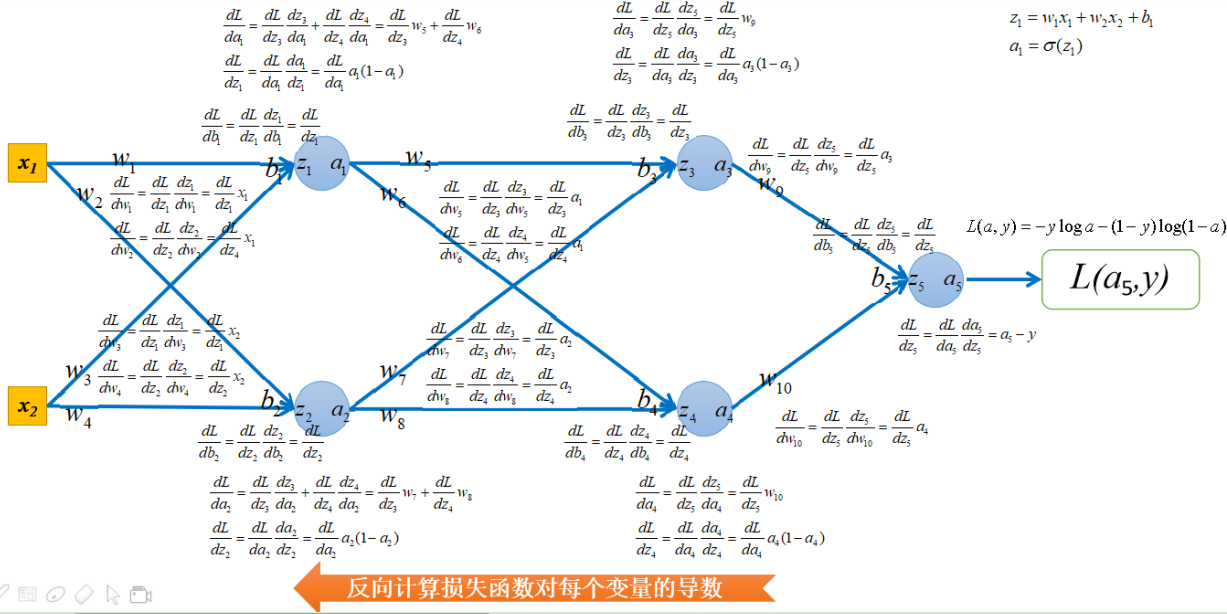
然后就可以更新w和b,更新模型了,即
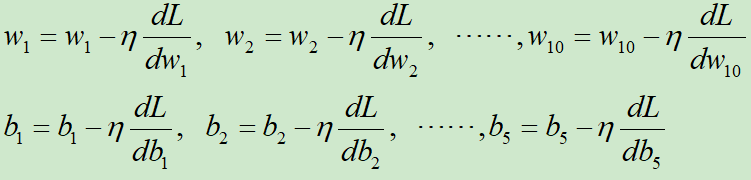
|
全连接神经网络的正、反向传播案例 |
假设最开始初始化所有w都等于0.5,所有的b都等于1,本轮训练样本为[(2,3),0],损失函数选用的对数损失,如下图所示:
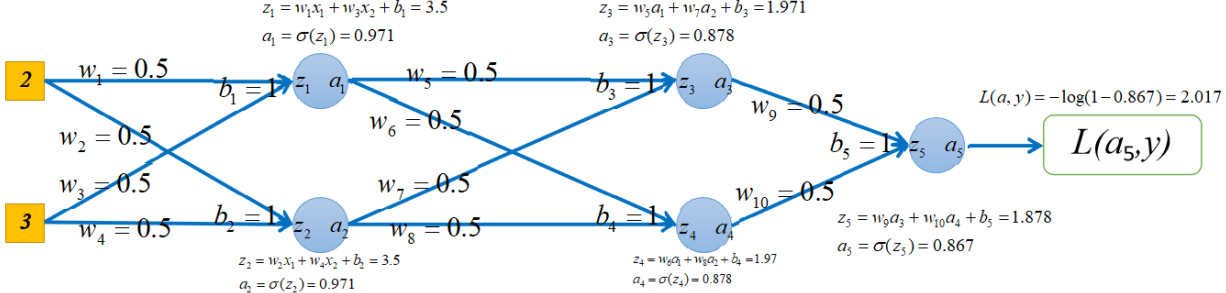
可以看出在当前模型参数下,正向传播后,损失为2.017
接下来,使用BP算法更新模型参数,如下图所示:
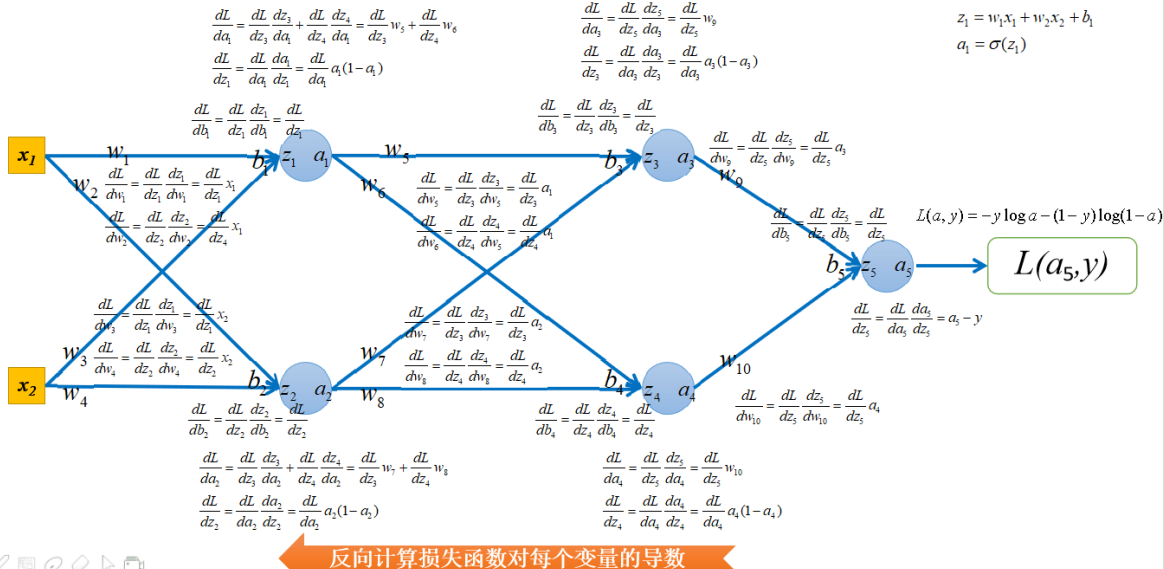

如果再进行正向传播计算损失的话,可以发现,损失从2.017降低到1.83:
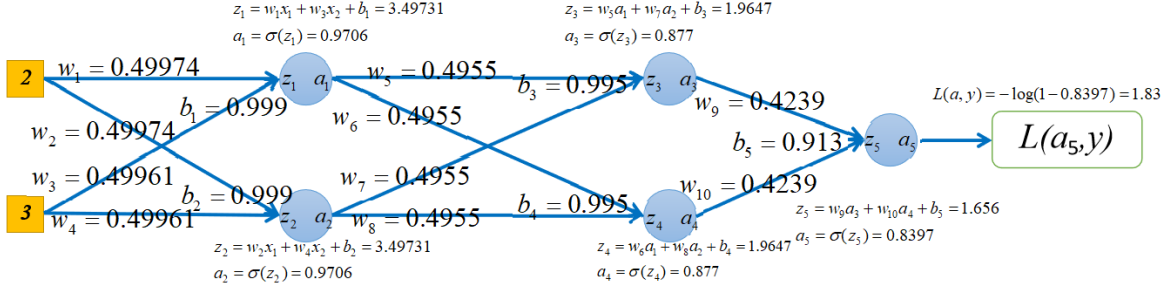
对应代码:
 View Code
View Code
|
参考资料 |
吴恩达机器学习

 浙公网安备 33010602011771号
浙公网安备 33010602011771号