程序员编程艺术第二十五章：Jon Bentley：90%无法正确实现二分查找

作者：July
出处：结构之法算法之道

引言

    Jon Bentley：90%以上的程序员无法正确无误的写出二分查找代码。也许很多人都早已听说过这句话，但我还是想引用《编程珠玑》上的如下几段文字： 

“二分查找可以解决（预排序数组的查找）问题：只要数组中包含T（即要查找的值），那么通过不断缩小包含T的范围，最终就可以找到它。一开始，范围覆盖整个数组。将数组的中间项与T进行比较，可以排除一半元素，范围缩小一半。就这样反复比较，反复缩小范围，最终就会在数组中找到T，或者确定原以为T所在的范围实际为空。对于包含N个元素的表，整个查找过程大约要经过log(2)N次比较。 
多数程序员都觉得只要理解了上面的描述，写出代码就不难了；但事实并非如此。如果你不认同这一点，最好的办法就是放下书本，自己动手写一写。试试吧。 
我在贝尔实验室和IBM的时候都出过这道考题。那些专业的程序员有几个小时的时间，可以用他们选择的语言把上面的描述写出来；写出高级伪代码也可以。考试结束后，差不多所有程序员都认为自己写出了正确的程序。于是，我们花了半个钟头来看他们编写的代码经过测试用例验证的结果。几次课，一百多人的结果相差无几：90%的程序员写的程序中有bug（我并不认为没有bug的代码就正确）。 
我很惊讶：在足够的时间内，只有大约10%的专业程序员可以把这个小程序写对。但写不对这个小程序的还不止这些人：高德纳在《计算机程序设计的艺术 第3卷 排序和查找》第6.2.1节的“历史与参考文献”部分指出，虽然早在1946年就有人将二分查找的方法公诸于世，但直到1962年才有人写出没有bug的二分查找程序。 ”——乔恩·本特利，《编程珠玑（第1版）》第35-36页。

    你能正确无误的写出二分查找代码么？不妨一试。

二分查找代码

     二分查找的原理想必不用多解释了，不过有一点必须提醒读者的是，二分查找是针对的排好序的数组。OK，纸上读来终觉浅，觉知此事要躬行。我先来写一份，下面是我写的一份二分查找的实现（之前去某一家公司面试也曾被叫当场实现二分查找，不过结果可能跟你一样，当时就未能完整无误写出），有任何问题或错误，恳请不吝指正：

//二分查找V0.1实现版
//copyright@2011 July
//随时欢迎读者找bug，email：zhoulei0907@yahoo.cn。

//首先要把握下面几个要点：
//right=n-1 => while(left <= right) => right=middle-1;
//right=n   => while(left <  right) => right=middle;
//middle的计算不能写在while循环外，否则无法得到更新。

int binary_search(int array[],int n,int value)
{
    int left=0;
    int right=n-1;
    //如果这里是int right = n 的话，那么下面有两处地方需要修改，以保证一一对应：
    //1、下面循环的条件则是while(left < right)
    //2、循环内当array[middle]>value 的时候，right = mid

    while (left<=right)          //循环条件，适时而变
    {
        int middle=left + ((right-left)>>1);  //防止溢出，移位也更高效。同时，每次循环都需要更新。

        if (array[middle]>value)
        {
            right =middle-1;   //right赋值，适时而变
        }
        else if(array[middle]<value)
        {
            left=middle+1;
        }
        else
            return middle;
        //可能会有读者认为刚开始时就要判断相等，但毕竟数组中不相等的情况更多
        //如果每次循环都判断一下是否相等，将耗费时间
    }
    return -1;
}

    简单测试下，运行结果如下所示（当然，一次测试正确不代表程序便0 bug了，且测试深度远远不够）：

 

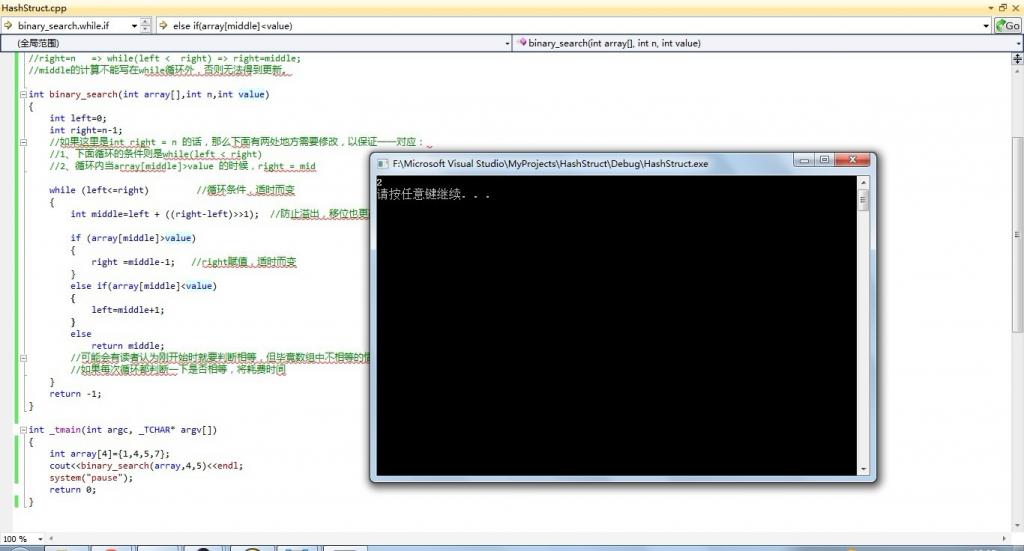
测试

    也许你之前已经把二分查找实现过很多次了，但现在不妨再次测试一下。关闭所有网页，窗口，打开记事本，或者编辑器，或者直接在本文评论下，不参考上面我写的或其他任何人的程序，给自己十分钟到N个小时不等的时间，立即编写一个二分查找程序。独立一次性正确写出来后，可以留下代码和邮箱地址，我给你传一份本blog的博文集锦CHM文件 && 十三个经典算法研究带标签+目录的PDF文档（你也可以去我的资源下载处下载：http://download.csdn.net/user/v_july_v）。

    当然，能正确写出来不代表任何什么，不能正确写出来亦不代表什么，仅仅针对Jon Bentley的言论做一个简单的测试而已。下一章，请见第二十六章：基于给定的文档生成倒排索引的编码与实践。谢谢。

总结

    本文发表后，马上就有很多朋友自己尝试了。根据从朋友们在本文评论下留下的代码，发现出错率最高的在以下这么几个地方：

 

1. 注释里已经说得很明白了，可还是会有不少朋友犯此类的错误：
   

   //首先要把握下面几个要点：
   //right=n-1 => while(left <= right) => right=middle-1;
   //right=n   => while(left <  right) => right=middle;
   //middle的计算不能写在while循环外，否则无法得到更新。

2. 还有一个最最常犯的错误是@土豆：
   middle= (left+right)>>1; 这样的话left与right的值比较大的时候，其和可能溢出。

    各位继续努力。

    updated：各位，可以到此处0积分下载本blog最新博文集锦第6期CHM文件：http://download.csdn.net/detail/v_july_v/4020172。

 

分享到： 

• 上一篇：编程艺术第二十三~四章&十一续：杨氏矩阵查找，倒排索引关键词Hash编码
• 下一篇：程序员编程艺术第二十六章：基于给定的文档生成倒排索引（含源码下载）

顶

42

踩

3

查看评论

64楼 natulis 2013-04-14 17:14发表 [回复]

发现个小细节问题，left + ((right-left)>>1)
位移的优先级比四则运算低，所以不用写这么多括号，我觉得写成left + (right - left >> 1)就行了，博主你看看行不

63楼 zhaojia1989 2013-03-26 16:00发表 [回复]

#include <iostream>
using namespace std;

int binary_search(int a[], int length, int dst)
{
int *p = a;
while (length != 0)
{
if (p[length/2] == dst)
return length/2;
if (p[length/2] > dst)
length /= 2;
else
{
length /= length;
p += length;
}
}
return -1;
}

int main()
{
int a[] = {1,2,3,4};
int rst = binary_search(a, 4, 3);
cout << rst << endl;
return 0;
}
为什么不考虑操作指针？

62楼 onehao 2013-02-20 22:12发表 [回复]

今天来跟着楼主一起学习，谢谢！

61楼 syzcch 2012-10-16 13:15发表 [回复]

确实 写出没bug的程序不容易

60楼 slayerxj 2012-10-12 14:16发表 [回复] [引用] [举报]

int binary_search(int array[], int n, int value)
{
    if ((array == NULL) || (n == 0)) {
        return -1;
    }
    if (array[0] == value) {
        return 0;
    }
    if (array[n] == value) {
        return n;
    }

    int left = 0;
    int right = n;
    int middle = n >> 1;
    while (right - left != 1) {
        if (value < array[middle]) {
            right = middle;
        } else if (value > array[middle]) {
            left = middle;
        } else {
            return middle;
        }
        middle = left + ((right - left) >> 1);
    }

    return -1;
}
int _tmain(int argc, _TCHAR* argv[])
{
    int array[] = {2, 4, 7, 11, 23, 57, 89, 46, 90};
    printf("%d\n", binary_search(array, 9, 2));
    printf("%d\n", binary_search(array, 9, 90));
    printf("%d\n", binary_search(array, 9, 57));
    printf("%d\n", binary_search(array, 9, 23));
    printf("%d\n", binary_search(array, 9, 26));
    getchar();
    return 0;
}