局部权重线性回归(Locally weighted linear regression)

在线性回归中，因为对參数个数选择的问题是在问题求解之前已经确定好的，因此參数的个数不能非常好的确定，假设參数个数过少可能拟合度不好，产生欠拟合(underfitting)问题，或者參数过多，使得函数过于复杂产生过拟合问题(overfitting)。因此本节介绍的局部线性回归(LWR)能够降低这种风险。

欠拟合与过拟合

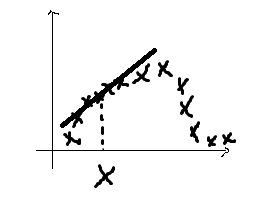
首先看以下的图 

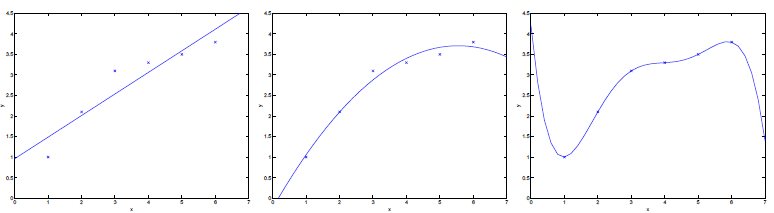
对于图中的一系列样本点，当我们採用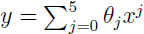y=θ0+θ1x形式的时候，我们可能产生最左边图形式的拟合曲线；假设我们採用y=θ0+θ1x+θ2x2时候，我们就能够产生中间的拟合曲线；假设採用形式，便会产生最右边的拟合曲线。从三张图中我们能够看出来，第一条曲线存在欠拟合问题，第三条的曲线存在过拟合问题。

局部权重线性回归(Locally weighted linear regression)

在主要的线性回归问题中，首先我们构造出预測函数h(x)，然后变化參数θ使得误差函数最小化，一旦θ确定，以后不会改变，全部的预測值都会使用着一个參数： 
 
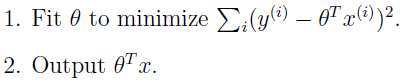
相比之下，局部权重线性回归方法运行例如以下的算法： 
 
 
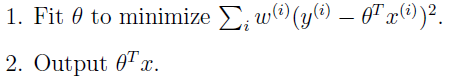
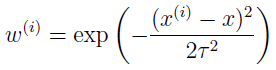
x代表须要预測的值的输入，x(i)表示的是训练的样本的输入值。从w(i)的表达式我们能够看出，（x(i)−x）2能够理解成训练值与预測值之间的距离，当距离越大w≈0，反之，距离越小，w≈1。因此，当距离须要计算的x非常远的训练样本值会在最小化时候变为0，而仅仅使用x周围的局部点预測线性函数。例如以下图 
 
w中的τ称为带宽(bandwidth)參数,能够控制x周围的概念，即控制距离x多远能够參与线性函数的预计，τ越大，參与的点越多，反之，參与的点越少。 
因为局部权重线性回归方法每个预測每个点时候都须要又一次计算一次 
θ的值，因此，算法费时间复杂度会非常高，是一种non-parametric算法。前面的基本线性回归是一种parametric学习算法。

个人博客：http://www.houlaizhexq.com     houlaizhexq.github.io