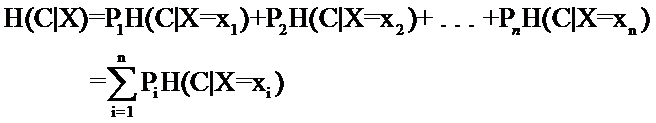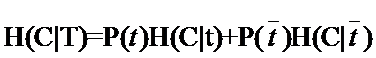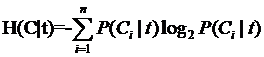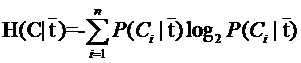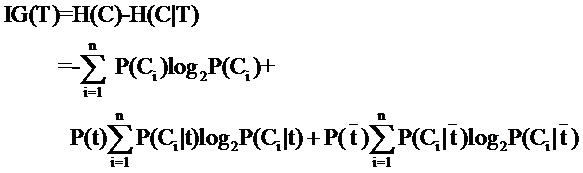特征选择方法之信息增益
前文提到过,除了开方检验(CHI)以外,信息增益(IG,Information Gain)也是非常有效的特征选择方法。但凡是特征选择,总是在将特征的重要程度量化之后再进行选择,而怎样量化特征的重要性,就成了各种方法间最大的不同。开方检验中使用特征与类别间的关联性来进行这个量化,关联性越强,特征得分越高,该特征越应该被保留。
在信息增益中,重要性的衡量标准就是看特征可以为分类系统带来多少信息,带来的信息越多,该特征越重要。
因此先回顾一下信息论中有关信息量(就是“熵”)的定义。说有这么一个变量X,它可能的取值有n多种,各自是x1,x2,……,xn,每一种取到的概率各自是P1,P2,……,Pn,那么X的熵就定义为:
意思就是一个变量可能的变化越多(反而跟变量详细的取值没有不论什么关系,仅仅和值的种类多少以及发生概率有关),它携带的信息量就越大(因此我一直认为我们的政策法规信息量非常大,由于它变化非常多,基本朝令夕改,笑)。
对分类系统来说,类别C是变量,它可能的取值是C1,C2,……,Cn,而每个类别出现的概率是P(C1),P(C2),……,P(Cn),因此n就是类别的总数。此时分类系统的熵就能够表示为:
有同学说不好理解呀,这样想就好了,文本分类系统的作用就是输出一个表示文本属于哪个类别的值,而这个值可能是C1,C2,……,Cn,因此这个值所携带的信息量就是上式中的这么多。
信息增益是针对一个一个的特征而言的,就是看一个特征t,系统有它和没它的时候信息量各是多少,两者的差值就是这个特征给系统带来的信息量,即增益。系统含有特征t的时候信息量非常好计算,就是刚才的式子,它表示的是包括全部特征时系统的信息量。
问题是当系统不包括t时,信息量如何计算?我们换个角度想问题,把系统要做的事情想象成这样:说教室里有非常多座位,学生们每次上课进来的时候能够随便坐,因而变化是非常大的(无数种可能的座次情况);可是如今有一个座位,看黑板非常清楚,听老师讲也非常清楚,于是校长的小舅子的姐姐的女儿托关系(真辗转啊),把这个座位定下来了,每次仅仅能给她坐,别人不行,此时情况如何?对于座次的可能情况来说,我们非常easy看出下面两种情况是等价的:(1)教室里没有这个座位;(2)教室里尽管有这个座位,但其它人不能坐(由于反正它也不能參与到变化中来,它是不变的)。
相应到我们的系统中,就是以下的等价:(1)系统不包括特征t;(2)系统尽管包括特征t,可是t已经固定了,不能变化。
我们计算分类系统不包括特征t的时候,就使用情况(2)来取代,就是计算当一个特征t不能变化时,系统的信息量是多少。这个信息量事实上也有专门的名称,就叫做“条件熵”,条件嘛,自然就是指“t已经固定“这个条件。
可是问题接踵而至,比如一个特征X,它可能的取值有n多种(x1,x2,……,xn),当计算条件熵而须要把它固定的时候,要把它固定在哪一个值上呢?答案是每一种可能都要固定一下,计算n个值,然后取均值才是条件熵。而取均值也不是简单的加一加然后除以n,而是要用每一个值出现的概率来算平均(简单理解,就是一个值出现的可能性比較大,固定在它上面时算出来的信息量占的比重就要多一些)。
因此有这样两个条件熵的表达式:
这是指特征X被固定为值xi时的条件熵,
这是指特征X被固定时的条件熵,注意与上式在意义上的差别。从刚才计算均值的讨论能够看出来,第二个式子与第一个式子的关系就是:
详细到我们文本分类系统中的特征t,t有几个可能的值呢?注意t是指一个固定的特征,比方他就是指关键词“经济”或者“体育”,当我们说特征“经济”可能的取值时,实际上仅仅有两个,“经济”要么出现,要么不出现。一般的,t的取值仅仅有t(代表t出现)和![]() (代表t不出现),注意系统包括t但t
不出现与系统根本不包括t但是两回事。
(代表t不出现),注意系统包括t但t
不出现与系统根本不包括t但是两回事。
因此固定t时系统的条件熵就有了,为了差别t出现时的符号与特征t本身的符号,我们用T代表特征,而用t代表T出现,那么:
与刚才的式子对比一下,含义非常清楚对吧,P(t)就是T出现的概率,![]() 就是T不出现的概率。这个式子能够进一步展开,当中的
就是T不出现的概率。这个式子能够进一步展开,当中的
还有一半就能够展开为:
因此特征T给系统带来的信息增益就能够写成系统原本的熵与固定特征T后的条件熵之差:
公式中的东西看上去非常多,事实上也都非常好计算。比方P(Ci),表示类别Ci出现的概率,事实上仅仅要用1除以类别总数就得到了(这是说你平等的看待每一个类别而忽略它们的大小时这样算,假设考虑了大小就要把大小的影响加进去)。再比方P(t),就是特征T出现的概率,仅仅要用出现过T的文档数除以总文档数就能够了,再比方P(Ci|t)表示出现T的时候,类别Ci出现的概率,仅仅要用出现了T而且属于类别Ci的文档数除以出现了T的文档数就能够了。
从以上讨论中能够看出,信息增益也是考虑了特征出现和不出现两种情况,与开方检验一样,是比較全面的,因而效果不错。但信息增益最大的问题还在于它仅仅能考察特征对整个系统的贡献,而不能详细到某个类别上,这就使得它仅仅适合用来做所谓“全局”的特征选择(指全部的类都使用同样的特征集合),而无法做“本地”的特征选择(每一个类别有自己的特征集合,由于有的词,对这个类别非常有区分度,对还有一个类别则无足轻重)。
看看,导出的过程事实上非常easy,没有什么神奇的对不正确。可有的学术论文里就喜欢把这样的本来非常直白的东西写得非常晦涩,仿佛仅仅有读者看不懂才是作者的真正成功。
咱们是新一代的学者,咱们没有知识不怕被别人看出来,咱们有知识也不怕教给别人。所以咱都把事情说简单点,说明确点,大家好,才是真的好。

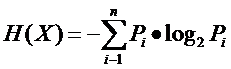
![clip_image002[4] clip_image002[4]](http://www.blogjava.net/images/blogjava_net/zhenandaci/WindowsLiveWriter/7fce385fe28b_D158/clip_image002%5B4%5D_thumb.gif)