【Java入门提高篇】Day33 Java容器类详解（十五）PriorityQueue详解

　　今天要介绍的是基础容器类（为了与并发容器类区分开来而命名的名字）中的另一个成员——PriorityQueue，它的大名叫做优先级队列，想必即使没有用过也该有所耳闻吧，什么？没。。没听过？emmm。。。那就更该认真看看了。

　　通过本篇你将了解到：

　　1、PriorityQueue是什么？

　　2、PriorityQueue的内部结构是什么？

　　3、二叉堆、大顶堆、小顶堆分别是什么？有什么特性？

　　4、小顶堆是如何实现的，如何用数组表示？

　　5、小顶堆的删除、插入操作是如何进行的？

　　6、PriorityQueue的源码解析。

　　7、PriorityQueue的应用场景。

一、PriorityQueue简介

　　PriorityQueue也是Queue的一个继承者，相比于一般的列表，它的特点便如它的名字一样，出队的时候可以按照优先级进行出队，所以不像LinkedList那样只能按照插入的顺序出队，PriorityQueue是可以根据给定的优先级顺序进行出队的。这里说的给定优先级顺序既可以是内部比较器，也可以是外部比较器。PriorityQueue内部是根据小顶堆的结构进行存储的，所谓小顶堆的意思，便是最小的元素总是在最上面，每次出队总是将堆顶元素移除，这样便能让出队变得有序，至于什么是小顶堆，后面会有详细介绍。

　　比如说，比较常见的场景就是任务队列，队列动态插入，后面的任务优先级高的需要被先执行，那么使用优先级队列就可以比较好的实现这样的需求。下面我们模拟一下这个场景：

public class PriorityQueueTest {
    public static void main(String[] args){
        // 传入外部比较器，
        //PriorityQueue<Task> taskQueue = new PriorityQueue<>(Comparator.comparingInt(Task::getPriority));
        //PriorityQueue<Task> taskQueue = new PriorityQueue<>((t1, t2) -> t1.getPriority() - t2.getPriority());
        PriorityQueue<Task> taskQueue = new PriorityQueue<>(new Comparator<Task>() {
            @Override
            public int compare(Task t1, Task t2) {
                return t1.getPriority() - t2.getPriority();
            }
        });

        // 添加六个任务
        taskQueue.add(new Task(1, "learn java"));
        taskQueue.add(new Task(3, "learn c++"));
        taskQueue.add(new Task(4, "learn c#"));
        taskQueue.add(new Task(2, "learn python"));
        taskQueue.add(new Task(2, "learn php"));
        taskQueue.add(new Task(5, "learn js"));

        // 出队
        while (!taskQueue.isEmpty()){
            System.out.println(taskQueue.poll());
        }
    }
}

class Task{
    /**
     * 任务优先级
     */
    private int priority;
    /**
     * 任务名称
     */
    private String taskName;

    public Task() {
    }

    public Task(int priority, String taskName) {
        this.priority = priority;
        this.taskName = taskName;
    }

    public int getPriority() {
        return priority;
    }

    public void setPriority(int priority) {
        this.priority = priority;
    }

    public String getTaskName() {
        return taskName;
    }

    public void setTaskName(String taskName) {
        this.taskName = taskName;
    }

    @Override
    public String toString() {
        return "Task{" +
                "priority=" + priority +
                ", taskName='" + taskName + '\'' +
                '}';
    }
}

　　输出如下：

Task{priority=1, taskName='learn java'}
Task{priority=2, taskName='learn python'}
Task{priority=2, taskName='learn php'}
Task{priority=3, taskName='learn c++'}
Task{priority=4, taskName='learn c#'}
Task{priority=5, taskName='learn js'}

　　可以看到，输出的时候是按照我们设定的优先级顺序进行输出的，由于默认的是小顶堆，所以这里Priority值小的会被先输出。

二、PriorityQueue的内部结构

　　上面已经提到了，PriorityQueue的内部结构其实是按照小顶堆的结构进行存储的，那么什么是小顶堆呢？说到小顶堆，还是先从堆开始介绍吧。

　　堆和栈一样是一种很基础的数据结构，在维基百科中的介绍如下：

堆（英语：Heap）是计算机科学中一类特殊的数据结构的统称。堆通常是一个可以被看做一棵树的数组对象。在队列中，调度程序反复提取队列中第一个作业并运行，因为实际情况中某些时间较短的任务将等待很长时间才能结束，或者某些不短小，但具有重要性的作业，同样应当具有优先权。堆即为解决此类问题设计的一种数据结构。

　　用图来表示的话就像这样：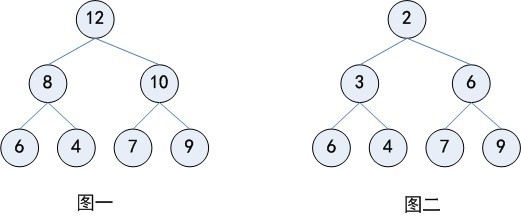

　　说完了堆，再来聊聊它的进化版——二叉堆，同样引用维基百科中的介绍：

二叉堆（英语：binary heap）是一种特殊的堆，二叉堆是完全二叉树或者是近似完全二叉树。二叉堆满足堆特性：父节点的键值总是保持固定的序关系于任何一个子节点的键值，且每个节点的左子树和右子树都是一个二叉堆。

当父节点的键值总是大于或等于任何一个子节点的键值时为最大堆。 当父节点的键值总是小于或等于任何一个子节点的键值时为最小堆。

　　其中，最大堆也叫做大顶堆或者大根堆，最小堆也叫做小顶堆或者小根堆。上面的图一其实就是一个大顶堆，而图二则是小顶堆。PriorityQueue是通过数组表示的小顶堆实现的，既然如此，PriorityQueue的排序特性自然与小顶堆的特性一致，下面便介绍小顶堆如何使用数组进行表示以及插入删除时的调整。

　　下面是一个由10，16，20，22，18，25，26，30，24，23构成的小顶堆：

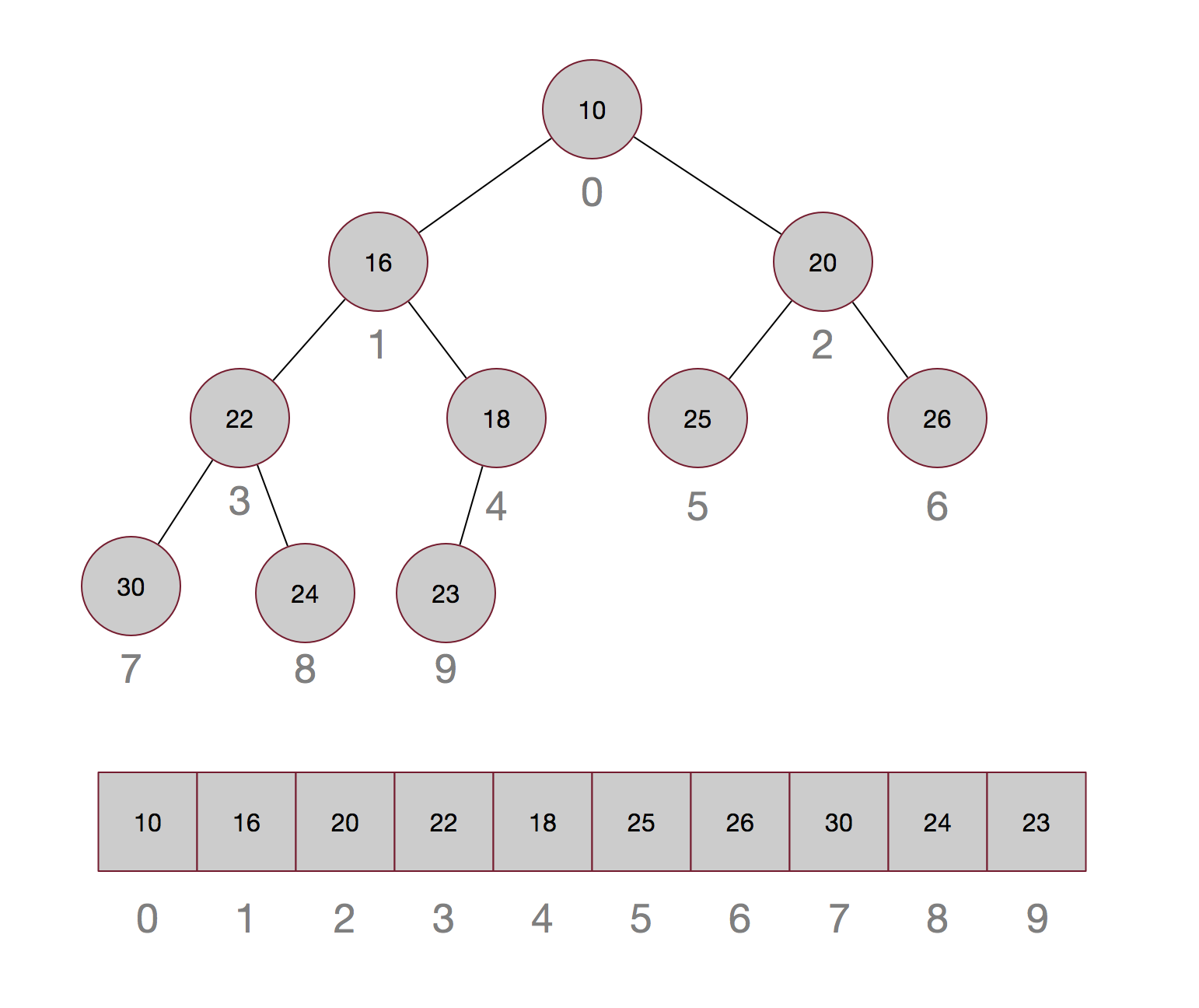　　将其从第一个元素开始依次从上到下，从左到右给每个元素添加一个序号，从0开始，这样就得到了相应元素在数组中的位置，而且这个序号是很有规则的，第k个元素的左孩子的序号为2k+1，右孩子的序号为2k+2，这样就很容易根据序号直接算出对应孩子的位置，时间复杂度为o(1)。这也就是为什么可以用数组来存储堆结构的原因了。

　　再来看看小顶堆是如何插入元素的，假设我们插入一个元素15：

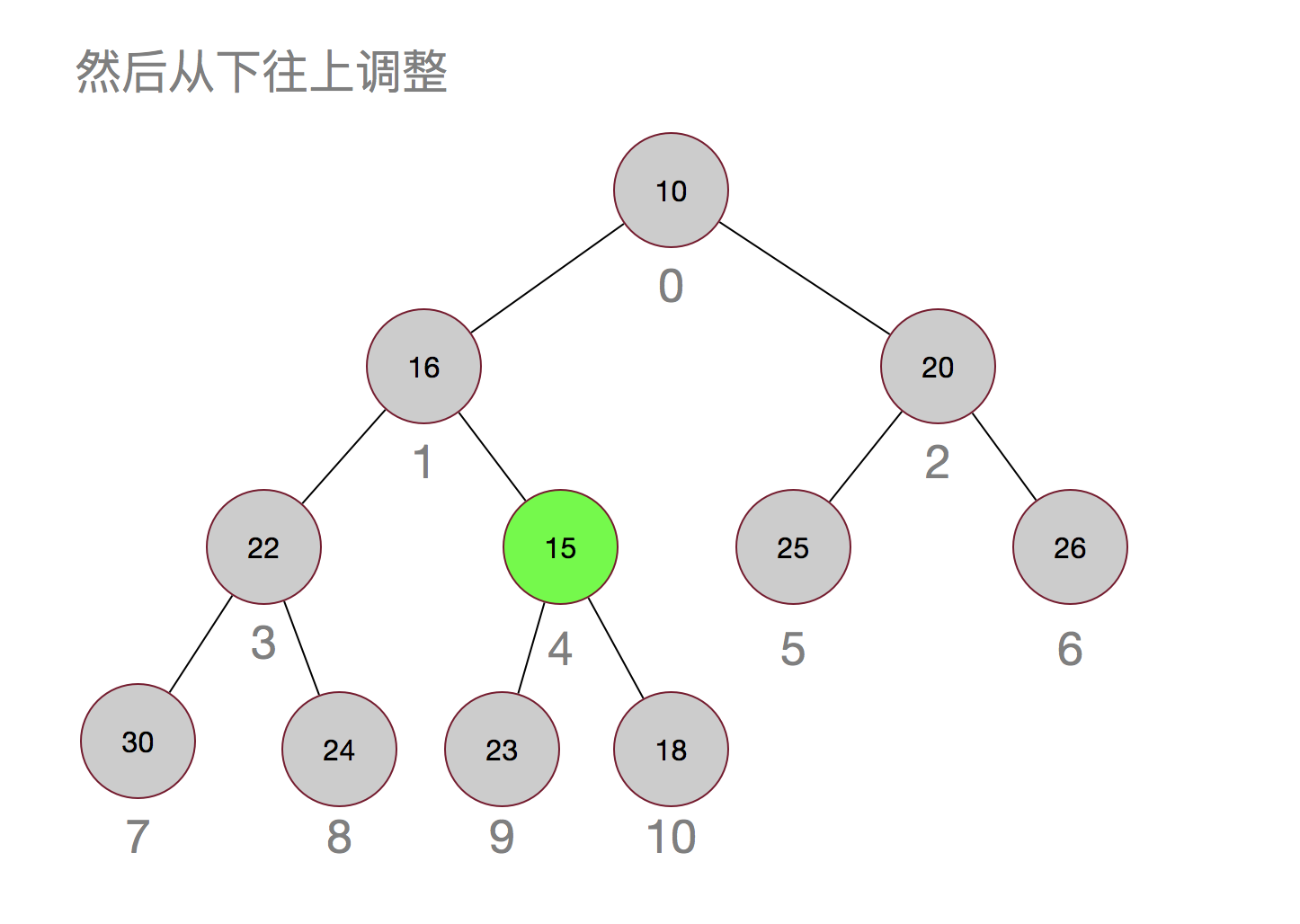
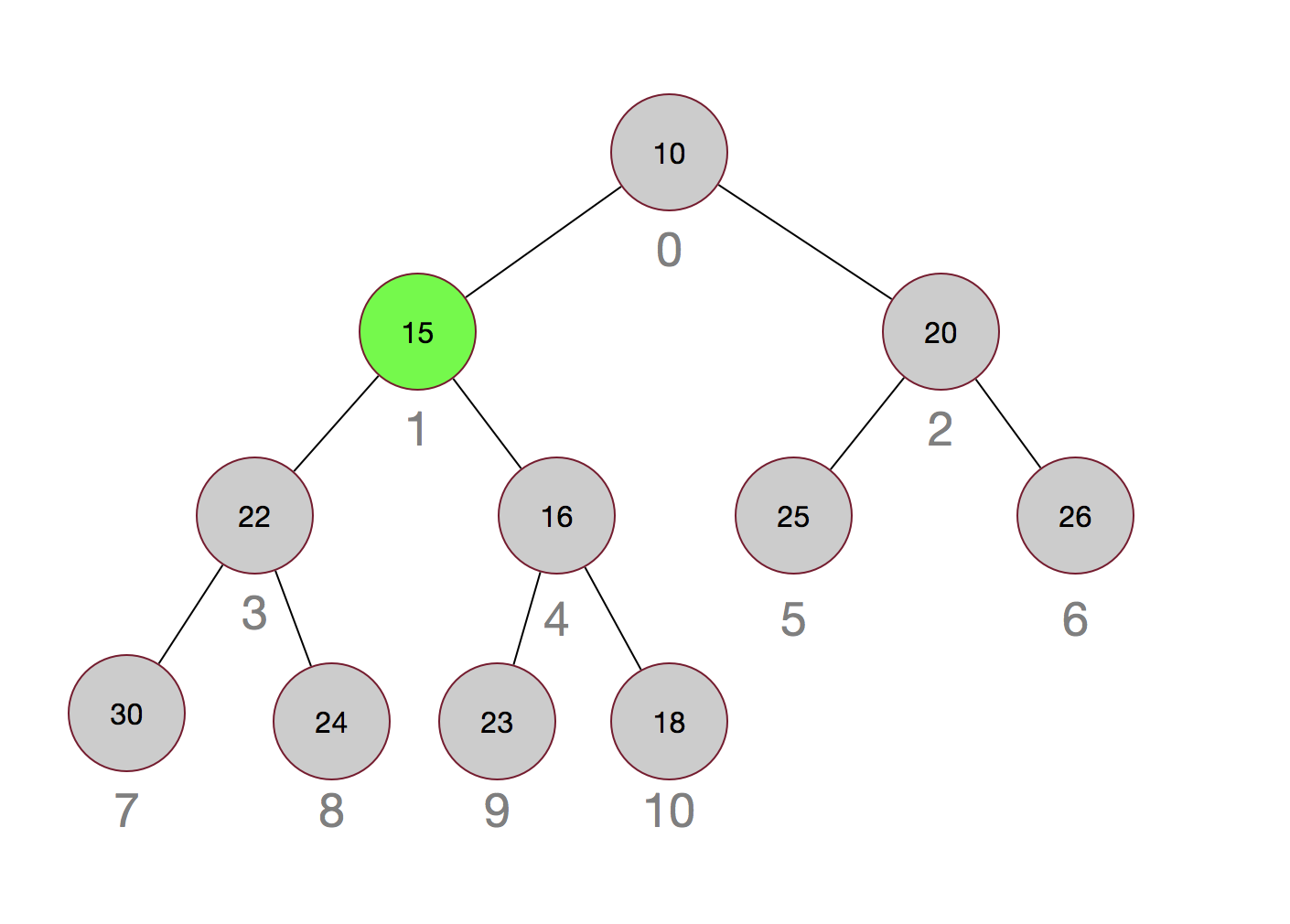
　　插入元素的调整其实很简单，就是先插入到最后，然后再依次与其父节点进行比较，如果小于其父节点，则互换，直到不需要调整或者父节点为null为止。

　　那再来看看移除元素：

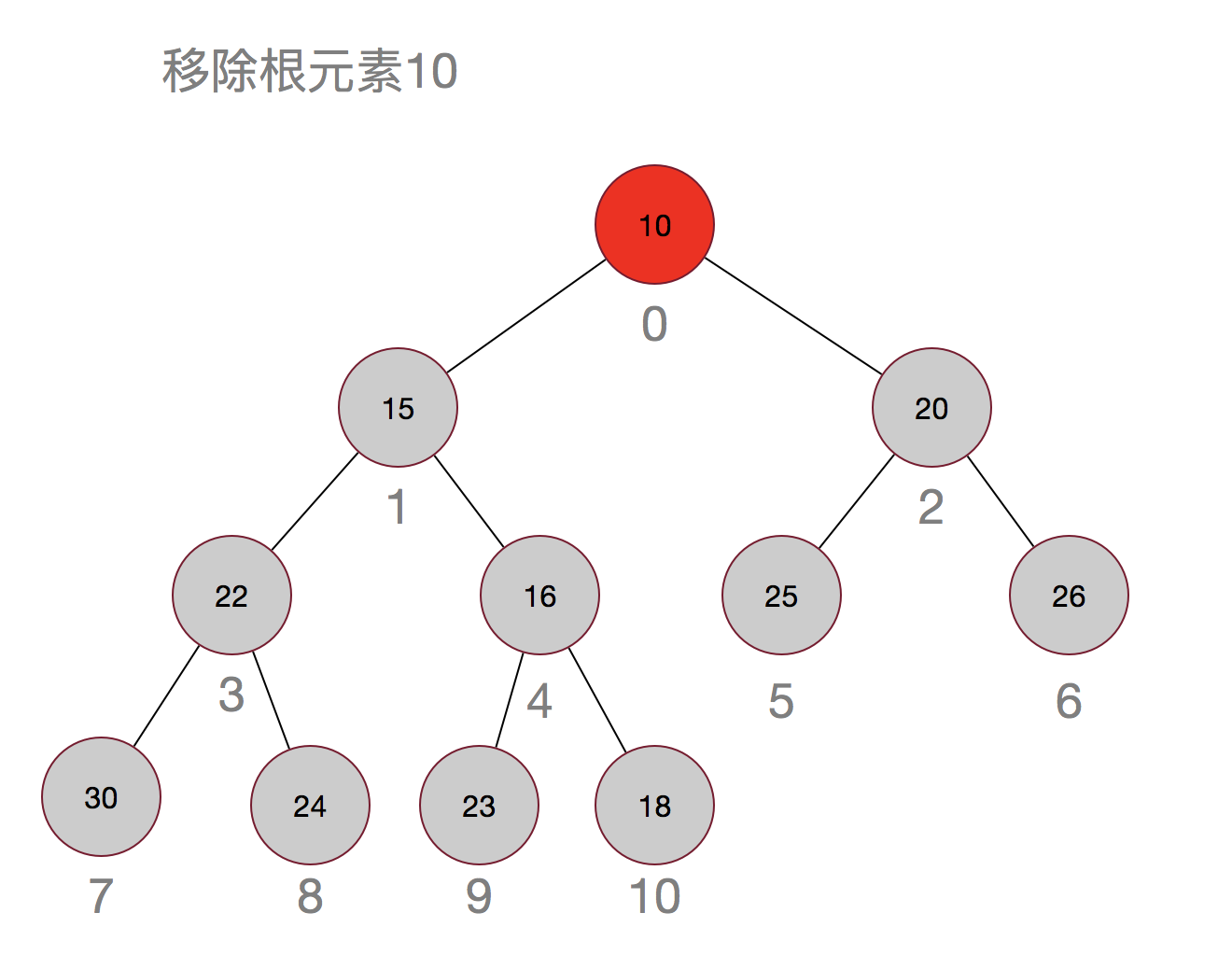
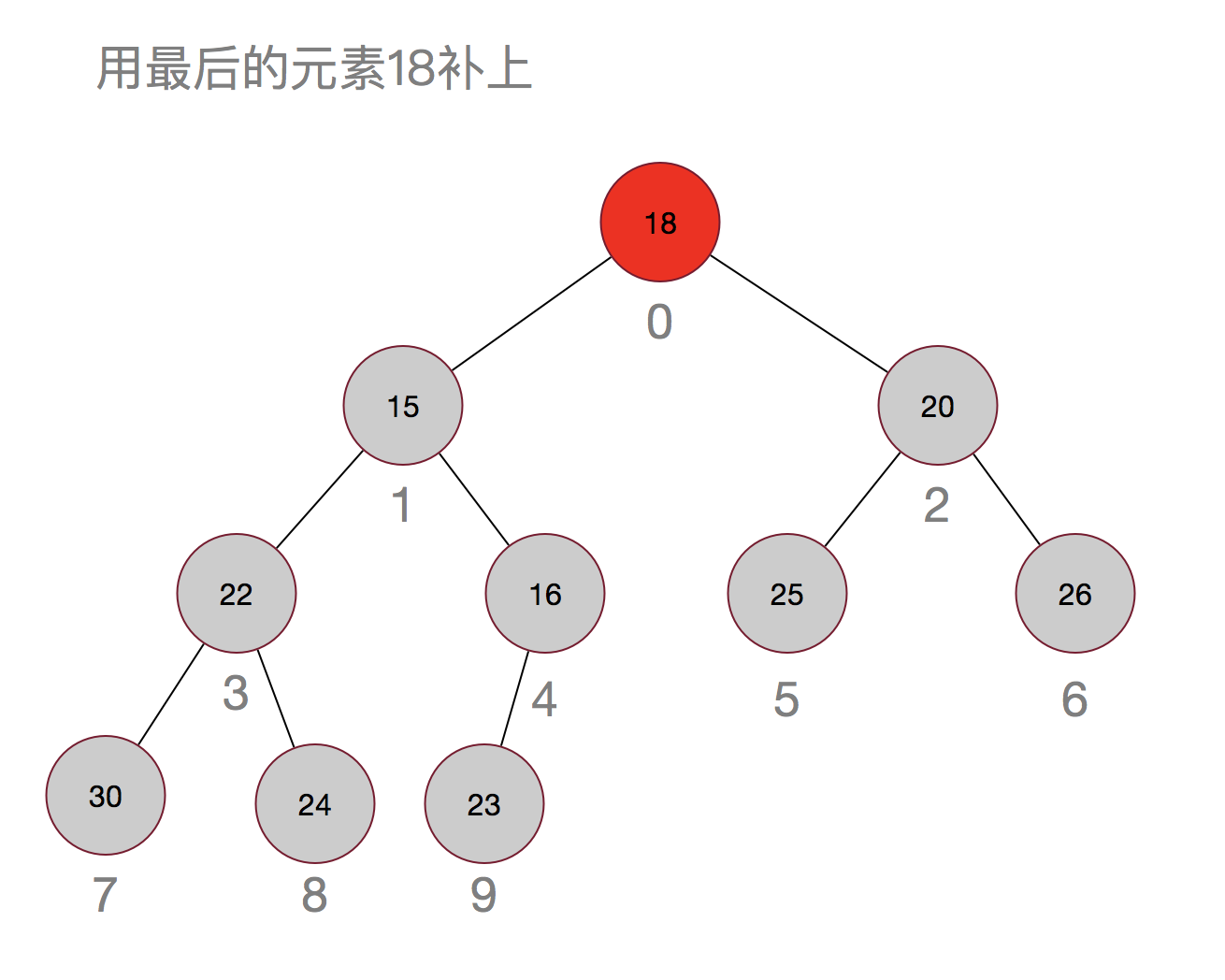
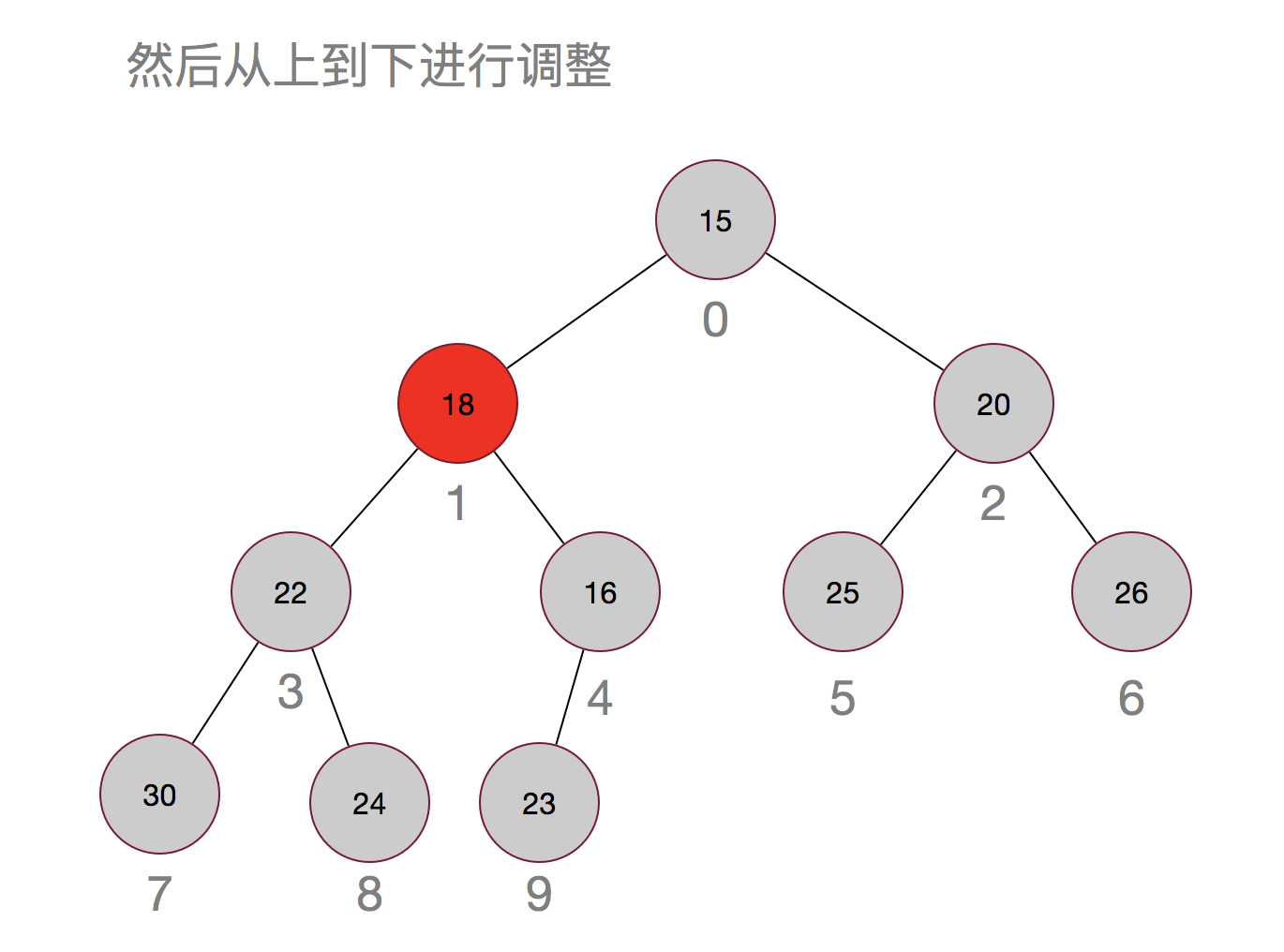
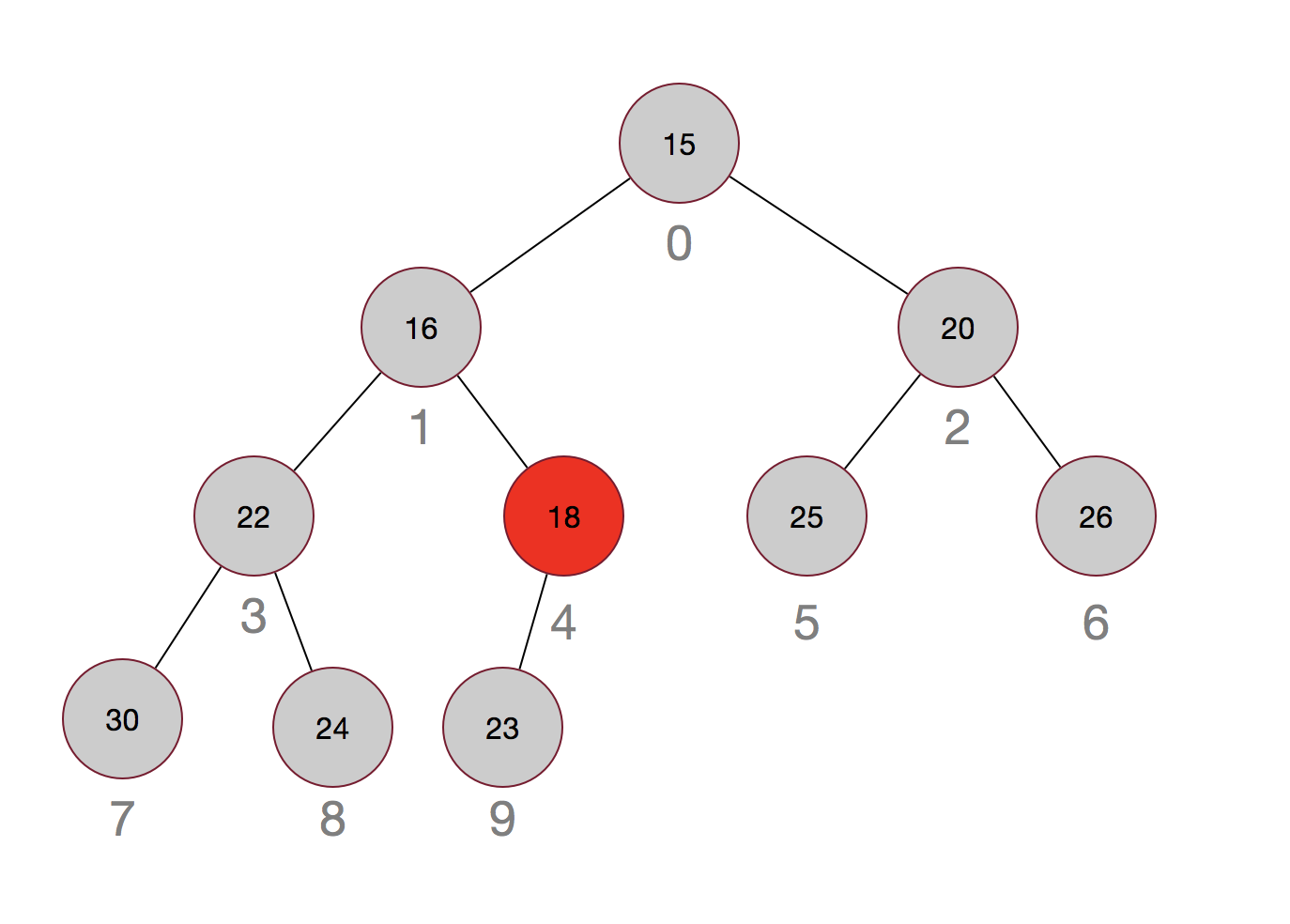
　　嗯，过程其实也很简单，先用最后的元素当替补，然后再从上往下进行调整。

三、PriorityQueue源码解析

　　小顶堆已经介绍完了，那PriorityQueue就没什么内容可讲了，嗯，那散了吧好了好了，不开玩笑了，接下来让我们一起来看看源码中是如何实现的。

　　先来继承结构：

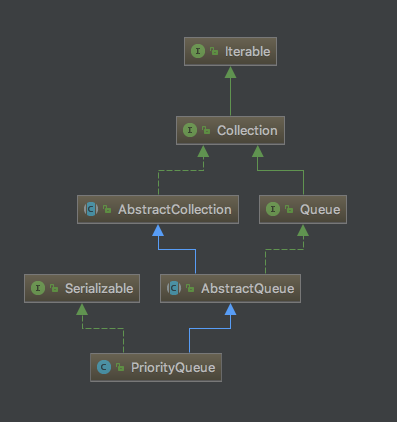
　　PriorityQueue继承自AbstractQueue，像这样的Abstract开头的抽象类，想必应该不陌生了，就是继承自指定接口然后进行了一些默认实现。

　　来看看PriorityQueue的内部成员：

    // 默认初始化容量
    private static final int DEFAULT_INITIAL_CAPACITY = 11;

    /**
     * 优先级队列是使用平衡二叉堆表示的: 节点queue[n]的两个孩子分别为
     * queue[2*n+1] 和 queue[2*(n+1)].  队列的优先级是由比较器或者
     * 元素的自然排序决定的， 对于堆中的任意元素n，其后代d满足：n<=d
     * 如果堆是非空的，则堆中最小值为queue[0]。
     */
    transient Object[] queue; 

    /**
     * 队列中元素个数
     */
    private int size = 0;

    /**
     * 比较器
     */
    private final Comparator<? super E> comparator;

    /**
     * 修改次数
     */
    transient int modCount = 0; 

　　可以看到内部使用的是一个Object数组进行元素的存储，并对该数组进行了详细的注释，所以不管是根据子节点找父节点，还是根据父节点找子节点都肥肠的方便。

　　再来看看它的构造函数，有点多，一共有六个构造函数：

    /**
     * 使用默认的容量（11）来构造一个空的优先级队列，使用元素的自然顺序进行排序（此时元素必须实现comparable接口）
     */
    public PriorityQueue() {
        this(DEFAULT_INITIAL_CAPACITY, null);
    }

    /**
     * 使用指定容量来构造一个空的优先级队列，使用元素的自然顺序进行排序（此时元素必须实现comparable接口）
     * 但如果指定的容量小于1则会抛出异常
     */
    public PriorityQueue(int initialCapacity) {
        this(initialCapacity, null);
    }

    /**
     * 使用默认的容量（11）构造一个优先级队列，使用指定的比较器进行排序
     */
    public PriorityQueue(Comparator<? super E> comparator) {
        this(DEFAULT_INITIAL_CAPACITY, comparator);
    }

    /**
     * 使用指定容量创建一个优先级队列，并使用指定比较器进行排序。
     * 但如果指定的容量小于1则会抛出异常
     */
    public PriorityQueue(int initialCapacity,
                         Comparator<? super E> comparator) {
        if (initialCapacity < 1)
            throw new IllegalArgumentException();
        this.queue = new Object[initialCapacity];
        this.comparator = comparator;
    }

    /**
     * 使用指定集合的所有元素构造一个优先级队列，
     * 如果该集合为SortedSet或者PriorityQueue类型，则会使用相同的顺序进行排序，
     * 否则，将使用元素的自然排序（此时元素必须实现comparable接口），否则会抛出异常
     * 并且集合中不能有null元素，否则会抛出异常
     */
    @SuppressWarnings("unchecked")
    public PriorityQueue(Collection<? extends E> c) {
        if (c instanceof SortedSet<?>) {
            SortedSet<? extends E> ss = (SortedSet<? extends E>) c;
            this.comparator = (Comparator<? super E>) ss.comparator();
            initElementsFromCollection(ss);
        }
        else if (c instanceof PriorityQueue<?>) {
            PriorityQueue<? extends E> pq = (PriorityQueue<? extends E>) c;
            this.comparator = (Comparator<? super E>) pq.comparator();
            initFromPriorityQueue(pq);
        }
        else {
            this.comparator = null;
            initFromCollection(c);
        }
    }

    /**
     * 使用指定的优先级队列中所有元素来构造一个新的优先级队列.  将使用原有顺序进行排序。
     */
    @SuppressWarnings("unchecked")
    public PriorityQueue(PriorityQueue<? extends E> c) {
        this.comparator = (Comparator<? super E>) c.comparator();
        initFromPriorityQueue(c);
    }

    /**
     * 根据指定的有序集合创建一个优先级队列，将使用原有顺序进行排序
     */
    @SuppressWarnings("unchecked")
    public PriorityQueue(SortedSet<? extends E> c) {
        this.comparator = (Comparator<? super E>) c.comparator();
        initElementsFromCollection(c);
    }

　　从集合中构造优先级队列的时候，调用了几个初始化函数：

    private void initFromPriorityQueue(PriorityQueue<? extends E> c) {
        if (c.getClass() == PriorityQueue.class) {
            this.queue = c.toArray();
            this.size = c.size();
        } else {
            initFromCollection(c);
        }
    }

    private void initElementsFromCollection(Collection<? extends E> c) {
        Object[] a = c.toArray();
        // If c.toArray incorrectly doesn't return Object[], copy it.
        if (a.getClass() != Object[].class)
            a = Arrays.copyOf(a, a.length, Object[].class);
        int len = a.length;
        if (len == 1 || this.comparator != null)
            for (int i = 0; i < len; i++)
                if (a[i] == null)
                    throw new NullPointerException();
        this.queue = a;
        this.size = a.length;
    }

    private void initFromCollection(Collection<? extends E> c) {
        initElementsFromCollection(c);
        heapify();
    }

　　initFromPriorityQueue即从另外一个优先级队列构造一个新的优先级队列，此时内部的数组元素不需要进行调整，只需要将原数组元素都复制过来即可。但是从其他非PriorityQueue的集合中构造优先级队列时，需要先将元素复制过来后再进行调整，此时调用的是heapify方法：

    private void heapify() {
        // 从最后一个非叶子节点开始从下往上调整
        for (int i = (size >>> 1) - 1; i >= 0; i--)
            siftDown(i, (E) queue[i]);
    }

    // 划重点了，这个函数即对应上面的元素删除时从上往下调整的步骤
    private void siftDown(int k, E x) {
        if (comparator != null)
            // 如果比较器不为null，则使用比较器进行比较
            siftDownUsingComparator(k, x);
        else
            // 否则使用元素的compareTo方法进行比较
            siftDownComparable(k, x);
    }

    private void siftDownUsingComparator(int k, E x) {
        // 使用half记录队列size的一半，如果比half小的话，说明不是叶子节点
        // 因为最后一个节点的序号为size - 1，其父节点的序号为(size - 2) / 2或者(size - 3 ) / 2
        // 所以half所在位置刚好是第一个叶子节点
        int half = size >>> 1;
        while (k < half) {
            // 如果不是叶子节点，找出其孩子中较小的那个并用其替换
            int child = (k << 1) + 1;
            Object c = queue[child];
            int right = child + 1;
            if (right < size &&
                comparator.compare((E) c, (E) queue[right]) > 0)
                c = queue[child = right];
            if (comparator.compare(x, (E) c) <= 0)
                break;
            // 用c替换
            queue[k] = c;
            k = child;
        }
        // 
        queue[k] = x;
    }
    // 同上，只是比较的时候使用的是元素的compareTo方法
    private void siftDownComparable(int k, E x) {
        Comparable<? super E> key = (Comparable<? super E>)x;
        int half = size >>> 1;        // 如果是非叶子节点则继续循环
        while (k < half) {
            int child = (k << 1) + 1;
            Object c = queue[child];
            int right = child + 1;
            if (right < size &&
                ((Comparable<? super E>) c).compareTo((E) queue[right]) > 0)
                c = queue[child = right];
            if (key.compareTo((E) c) <= 0)
                break;
            queue[k] = c;
            k = child;
        }
        queue[k] = key;
    }

　　这里可能一眼看过去有点难以理解，嗯，那就多看两眼吧。

　　siftDown方法是这里面比较重要的方法之一，有两个参数，一个是序号k，另一个是元素x，这个方法的作用，便是把x从k开始往下调整，使得在节点k在其子树的每相邻层中，父节点都小于其子节点。所以heapify的作用就比较明显了，从最后一个非叶子节点开始，从下往上依次调整其子树，使得最终得到的树里，根节点是最小的。这里要先理解一下为什么heapify中i的初始值要设置为(size >>> 1) - 1。因为这是最后一个非叶子节点的位置，不信的话可以随便画几个图验证一下，至于在siftDownUsingComparator方法中，int half = size >>> 1;这里half则是第一个叶子节点的位置，小于这个序号的节点都是非叶子节点，这里也可以画图验证，当然，注释中我已经做了解释。

　　说了这么多，也许还是不太明白，以集合{14,7,12,6,9,4,17,23,10,15,3}为例画个图吧：

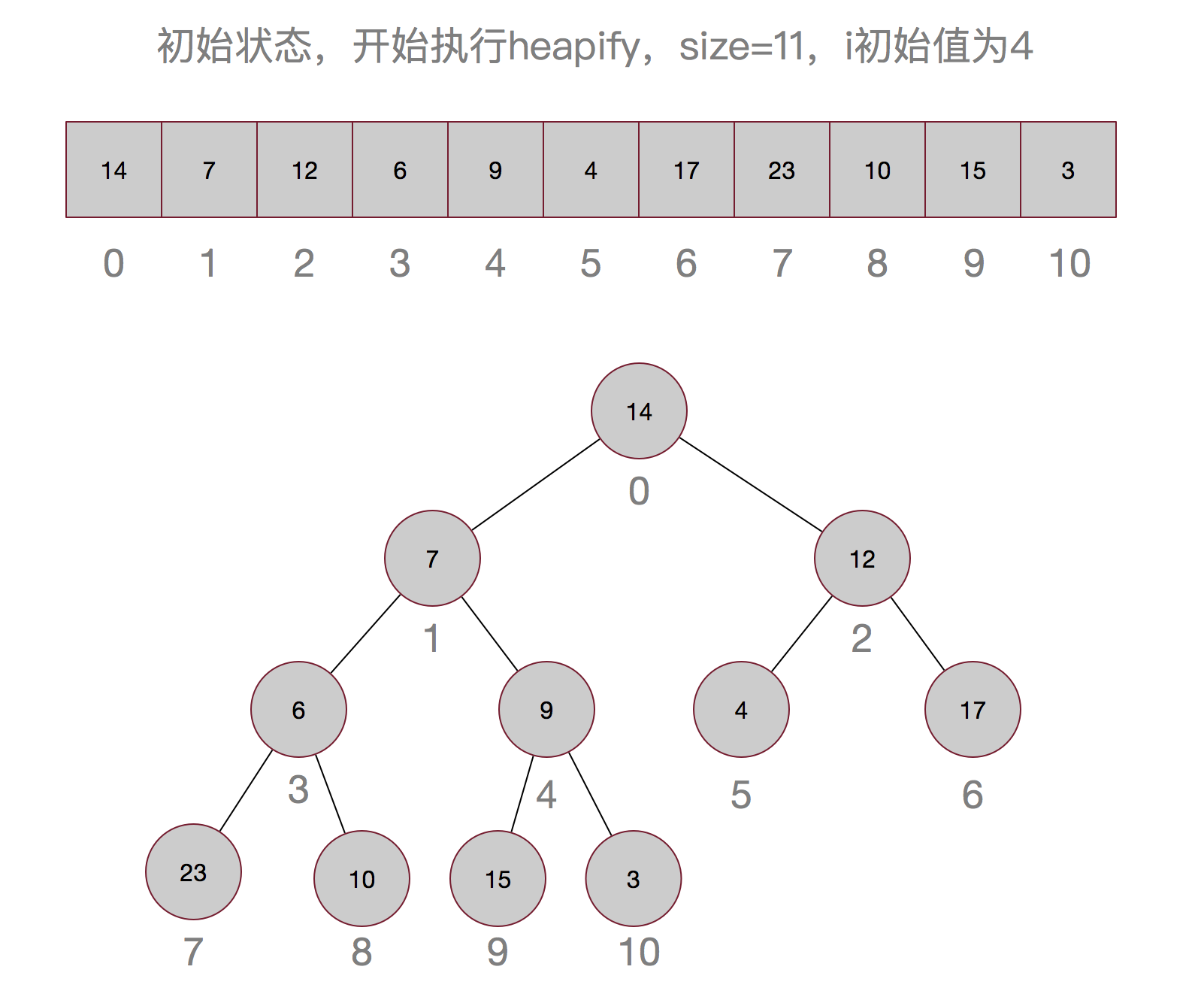
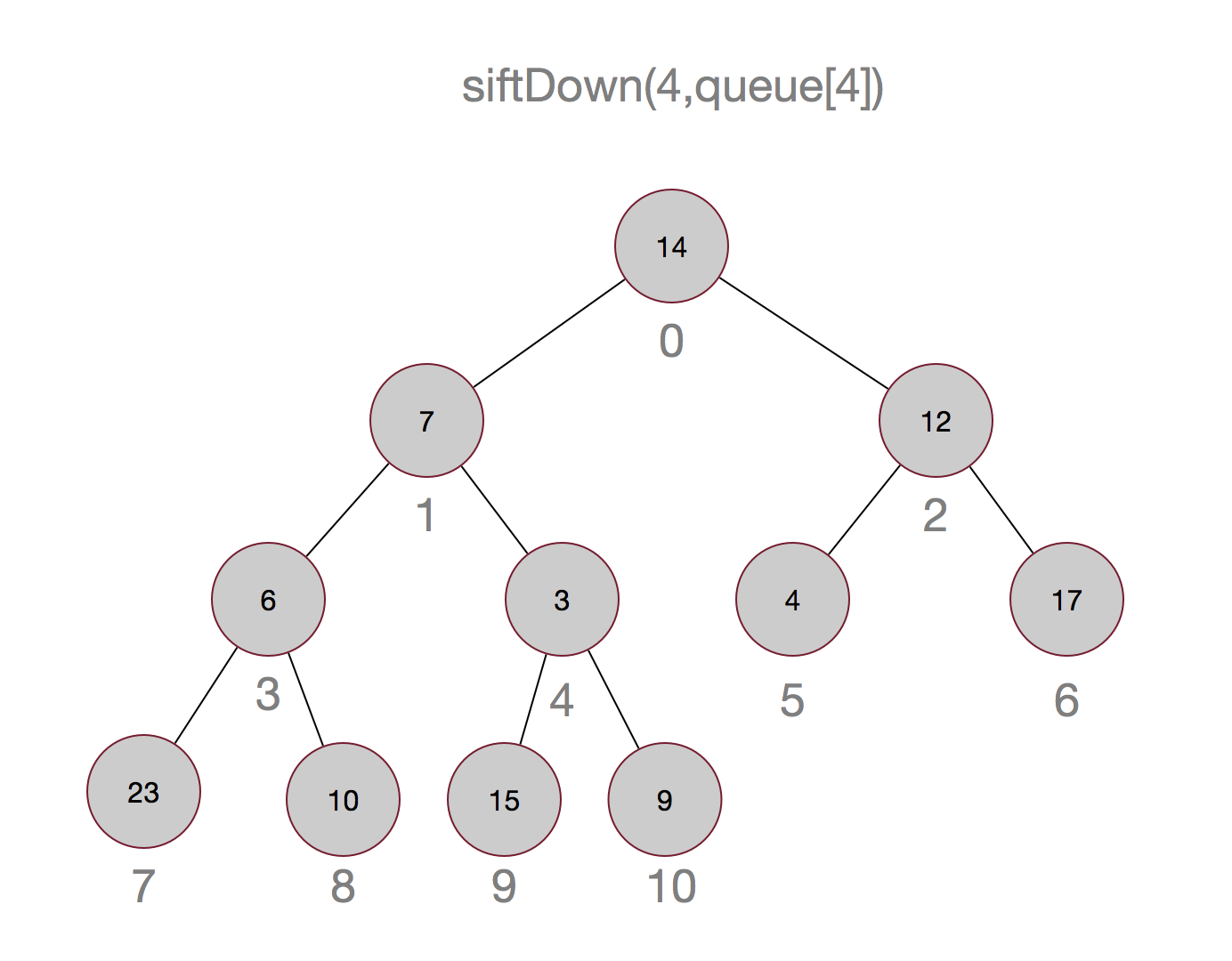
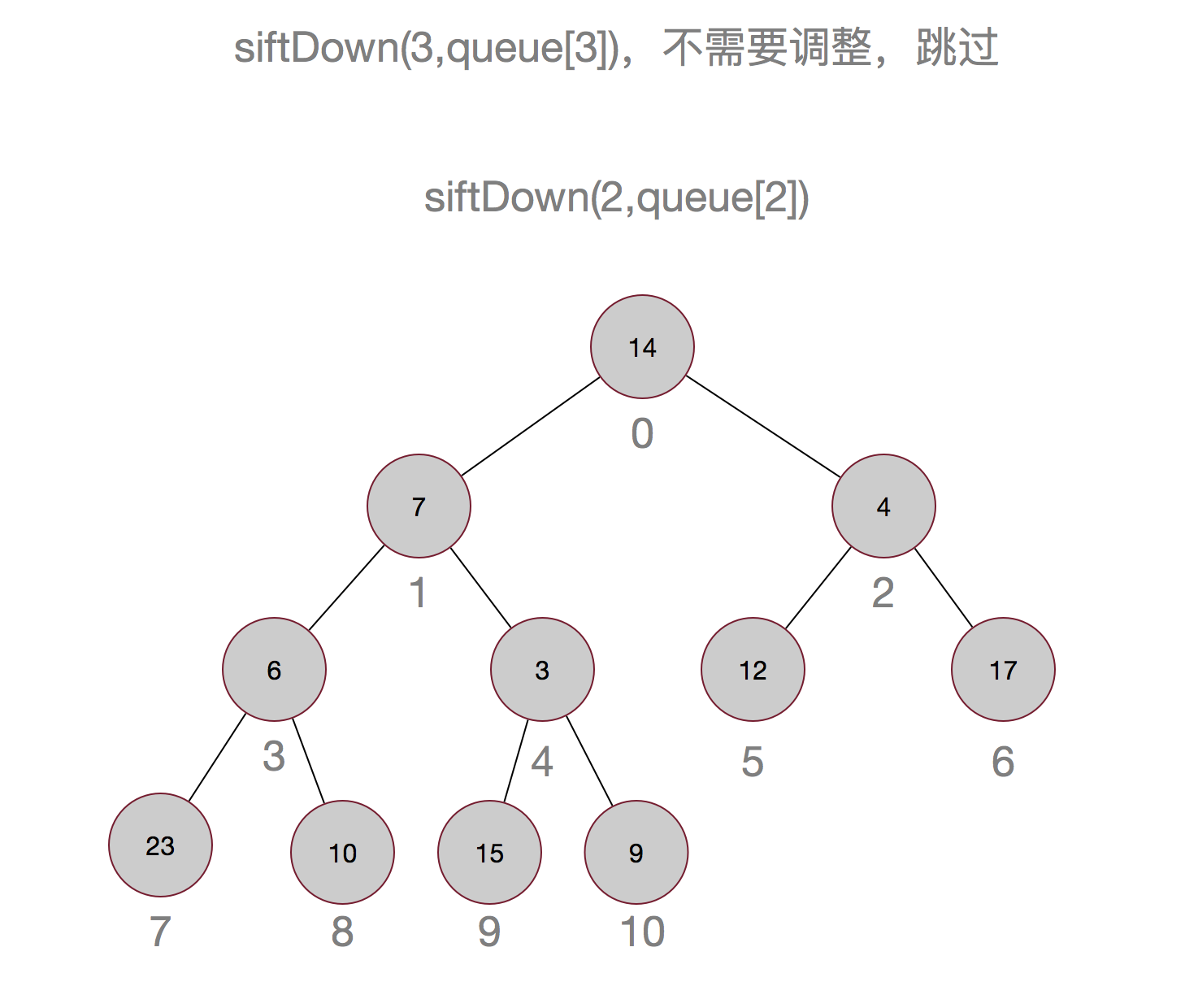
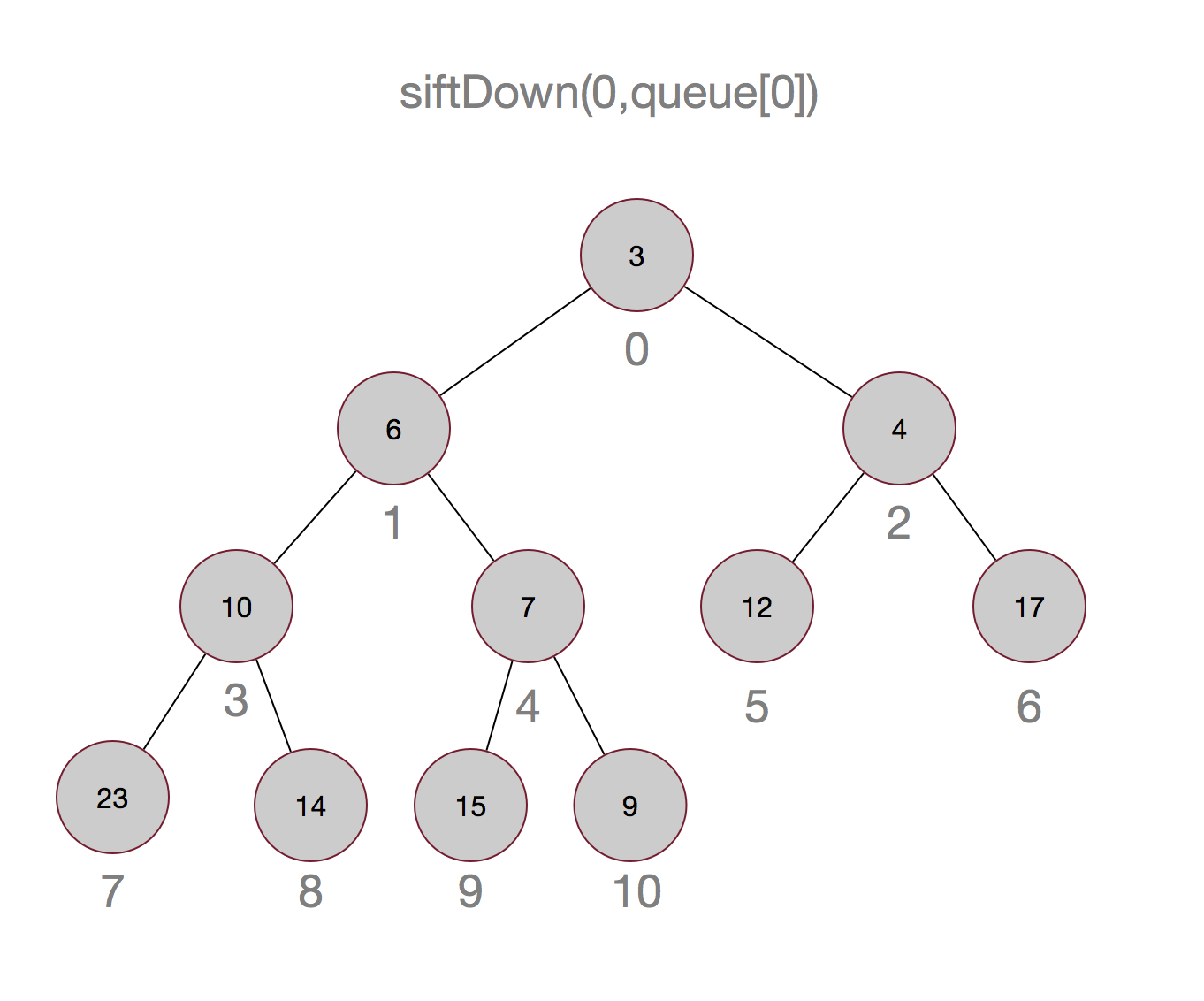
　　嗯，这样最小的元素就被顶上去了，有没有觉得有点像冒泡排序，嗯，确实有点像。

　　siftDown说完了，再来看一眼siftUp吧，这里操作是十分类似的。

    private void siftUp(int k, E x) {
        if (comparator != null)
            siftUpUsingComparator(k, x);
        else
            siftUpComparable(k, x);
    }

    @SuppressWarnings("unchecked")
    private void siftUpComparable(int k, E x) {
        Comparable<? super E> key = (Comparable<? super E>) x;
        while (k > 0) {
            int parent = (k - 1) >>> 1;
            Object e = queue[parent];
            if (key.compareTo((E) e) >= 0)
                break;
            queue[k] = e;
            k = parent;
        }
        queue[k] = key;
    }

    @SuppressWarnings("unchecked")
    private void siftUpUsingComparator(int k, E x) {
        while (k > 0) {
            int parent = (k - 1) >>> 1;
            Object e = queue[parent];
            if (comparator.compare(x, (E) e) >= 0)
                break;
            queue[k] = e;
            k = parent;
        }
        queue[k] = x;
    }

　　嗯，相信如果理解了siftDown的话，这里应该就不难理解了吧，如果还有疑问，欢迎留言。

　　再来看看几个常用的方法：

    public boolean add(E e) {
        return offer(e);
    }

    public boolean offer(E e) {
        if (e == null)
            throw new NullPointerException();
        modCount++;
        int i = size;
        if (i >= queue.length)
            grow(i + 1);
        size = i + 1;
        if (i == 0)
            queue[0] = e;
        else
            siftUp(i, e);
        return true;
    }
    // 扩容函数
    private void grow(int minCapacity) {
        int oldCapacity = queue.length;
        // 如果当前容量比较小（小于64）的话进行双倍扩容，否则扩容50%
        int newCapacity = oldCapacity + ((oldCapacity < 64) ?
                                         (oldCapacity + 2) :
                                         (oldCapacity >> 1));
        // 如果发现扩容后溢出了，则进行调整
        if (newCapacity - MAX_ARRAY_SIZE > 0)
            newCapacity = hugeCapacity(minCapacity);
        queue = Arrays.copyOf(queue, newCapacity);
    }
    private static int hugeCapacity(int minCapacity) {
        if (minCapacity < 0) // overflow
            throw new OutOfMemoryError();
        return (minCapacity > MAX_ARRAY_SIZE) ?
            Integer.MAX_VALUE :
            MAX_ARRAY_SIZE;
    }

    public boolean contains(Object o) {
        return indexOf(o) != -1;
    }

    private int indexOf(Object o) {
        if (o != null) {
            // 查找时需要进行全局遍历，比搜索二叉树的查找效率要低
            for (int i = 0; i < size; i++)
                if (o.equals(queue[i]))
                    return i;
        }
        return -1;
    }

    public E poll() {
        if (size == 0)
            return null;
        int s = --size;
        modCount++;
        E result = (E) queue[0];
        E x = (E) queue[s];
        queue[s] = null;
        if (s != 0)
            siftDown(0, x);
        return result;
    }

　　这里对照一下最开始说的小顶堆的插入和移除就能比较好的理解了。

　　最后源码中还有一个remove方法，需要稍微说明一下：

    // 这里不是移除堆顶元素，而是移除指定元素
    public boolean remove(Object o) {
        // 先找到该元素的位置
        int i = indexOf(o);
        if (i == -1)
            return false;
        else {
            removeAt(i);
            return true;
        }
    }
    // 移除指定序号的元素
    private E removeAt(int i) {
        // assert i >= 0 && i < size;
        modCount++;
        // s为最后一个元素的序号
        int s = --size;
        if (s == i) 
            queue[i] = null;
        else {
            // moved记录最后一个元素的值
            E moved = (E) queue[s];
            queue[s] = null;
            // 用最后一个元素代替要移除的元素，并向下进行调整
            siftDown(i, moved);
            // 如果向下调整后发现moved还在该位置，则再向上进行调整
            if (queue[i] == moved) {
                siftUp(i, moved);
                if (queue[i] != moved)
                    return moved;
            }
        }
        return null;
    }

　　当移除的不是堆顶元素的时候，同样先用最后一个元素代替，然后先从被移除的位置开始向下调整，如果发现没有改动，则再向上调整。

四、PriorityQueue的应用场景

　　最后，来聊聊PriorityQueue的应用场景，由于内部是用数组实现的小顶堆，所以堆适用的场景它都适用，比如典型的从n个元素中取出最小（最大）的前k个，这样的场景适用PriorityQueue就能以比较小的空间代价和还算ok的时间代价进行实现，另外，优先级队列适用场景的特点便是需要动态插入元素，并且元素有优先级，需要根据一定的规则进行优先级排序。

　　下面以从10000个整数中取出最大的10个整数为例进行介绍。

public class Test {
    public static void main(String[] args){
        ArrayList<Integer> integers = new ArrayList<>(10000);
        Random random = new Random();
        for (int i = 0; i < 10000; i++) {
            Integer integer = random.nextInt();
            if (!integers.contains(integer))
                integers.add(integer);
        }
        Integer[] largest = getLargest10(integers);
        for (Integer i : largest){
            System.out.print(i + " ");
        }

        System.out.println();
        
        // 验证一下是否是最大的前10个
        integers.sort(Comparator.comparingInt(Integer::intValue));
        ArrayList<Integer> largest2 = new ArrayList<>(10);
        for (int i = integers.size() - 1; i >= integers.size() - 10; i--){
            largest2.add(integers.get(i));
        }

        // 在largest数组中查找
        System.out.println(Arrays.asList(largest).containsAll(largest2)); 
    }

    public static Integer[] getLargest10(ArrayList<Integer> integers){
        PriorityQueue<Integer> queue = new PriorityQueue<>(10);
        for (Integer integer : integers){
            queue.add(integer);
            if (queue.size() > 10){
                queue.poll();
            }
        }
        return queue.toArray(new Integer[10]);
    }
}

　　输出如下，由于是取的随机数，所以每个人的输出都会不一样。

2143974860 2143998490 2144350843 2145111627 2144739333 2145674658 2144667271 2145543903 2147209906 2145466260 
true

　　最后，我们来回答一下开头的问题：

　　1、PriorityQueue是什么？PriorityQueue是优先级队列，取出元素时会根据元素的优先级进行排序。

　　2、PriorityQueue的内部结构是什么？PriorityQueue内部是一个用数组实现的小顶堆。

　　3、二叉堆、大顶堆、小顶堆分别是什么？有什么特性？二叉堆是完全二叉树或者近完全二叉树，大顶堆即所有父节点大于子节点，小顶堆即所有父节点小于子节点。

　　4、小顶堆是如何实现的，如何用数组表示？小顶堆是用二叉树实现的，用数组表示时，父节点n的左孩子为2n+1，右孩子的序号为2n+2。

　　5、小顶堆的删除、插入操作是如何进行的？小顶堆删除堆顶元素后用最后一个元素替补，然后从上往下调整，插入一个元素时，先放到最后的位置，然后再从下往上调整。

　　6、PriorityQueue的源码解析。如上。

　　7、PriorityQueue的应用场景。适用于需要动态插入元素，且元素有优先级顺序的场景。

　　到此，本篇圆满结束。如果觉得还不错的话，记得动动小手点个赞，也欢迎关注博主，你们的支持是我写出更好博客的动力。

　　有兴趣对Java进行更深入学习和交流的小伙伴，欢迎加入QQ群交流：529253292