GAMES101作业1：旋转与投影
学习和了解矩阵的基本使用后，准备做布置的第一次作业，巩固一下对相关知识的理解。
题目：给定三维下三个点 v0(2.0, 0.0, −2.0), v1(0.0, 2.0, −2.0), v2(−2.0, 0.0, −2.0)，需要将这三个点的坐标变换为屏幕坐标并在屏幕上绘制出对应的线框三角形。
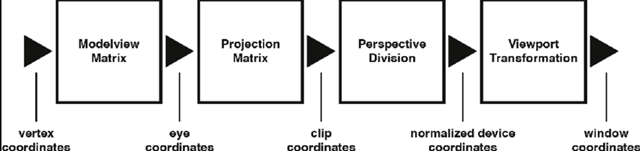
我们先看一下从模型空间 到 屏幕空间，都经历了哪些步骤。
（图片来源：《Fundamentals of Computer Graphics》 插图7.2）
经过了：模型 –> 世界 –> 观察（相机） –> 裁剪 –> 屏幕 的变换。
作业要求的 get_model_matrix 矩阵，需要绕 Z 轴进行旋转，我们只需要将旋转角度（angle）转为弧度（radian）,然代入对应的绕 Z 轴旋转矩阵即可（旋转矩阵如下图所示）
【角度】 转为 【弧度】 angle / 180 * PI，得到弧度 θ
Matrix_rotation_z = [
cos(θ), –sin(θ), 0, 0,
sin(θ), cos(θ), 0, 0,
0, 0, 1, 0,
0, 0, 0, 1
]
get_projection_matrix 按要求需要返回透视投影的矩阵，我们可以考虑先将透视的平截（锥）体压成立方体（这样就跟正交投影后续的计算一样了）
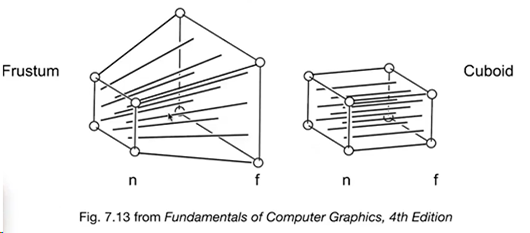
左边是平锥（截）体，右边是立方体，图中标示的 n、f分别为近裁剪平面（near clip plan）、远裁剪平面（far clip plan）距离相机 Z 轴的距离。
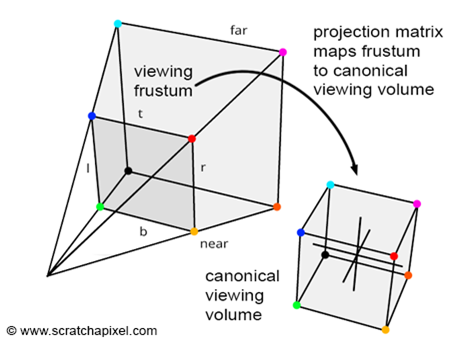
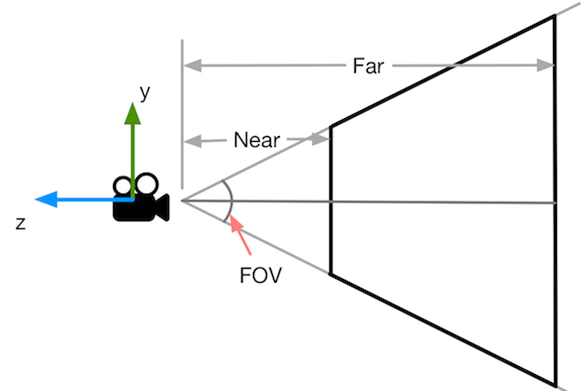
已知相机的垂直视场角 FOV（field of view），以及 near、far、aspect_ratio（屏幕宽高比 w / h = aspect_ratio），求图中四个顶点（ l、t、r、b）
t（top） = – near * tan(fov / 2)
b（bottom） = –t
l（left）= –t * aspect_ratio （w/h = l / t 可以推出 l = aspect_ratio * t，其中 X 轴方向朝向）
r（right） = –l
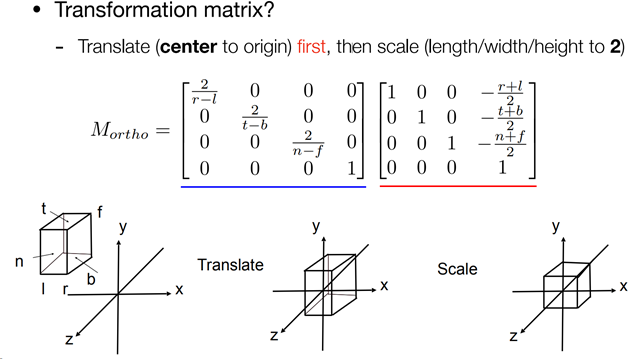
正交视图立方体转为单位立方体的变换矩阵（f = far， n = near）
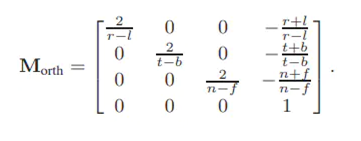
视锥体压成长方体的矩阵 （f = far， n = near） —— far clip plan 处的点 p1 在 near clip plan 处的位置 p2，远处点的 z 轴不变，中心点不变，唯一就是 x、y会变
推导过程比较复杂，详情可参考：
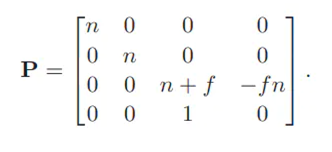
这样就可以推出透视投影矩阵 Mper = Morth * P
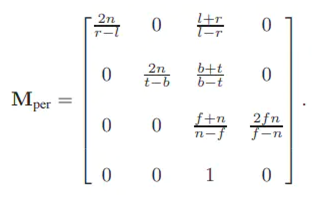
所以最终的透视投影矩阵可以有二种写法，一种是直接用最后的公式 Mper，另外一种就是用Morth * P（两者是等价的）
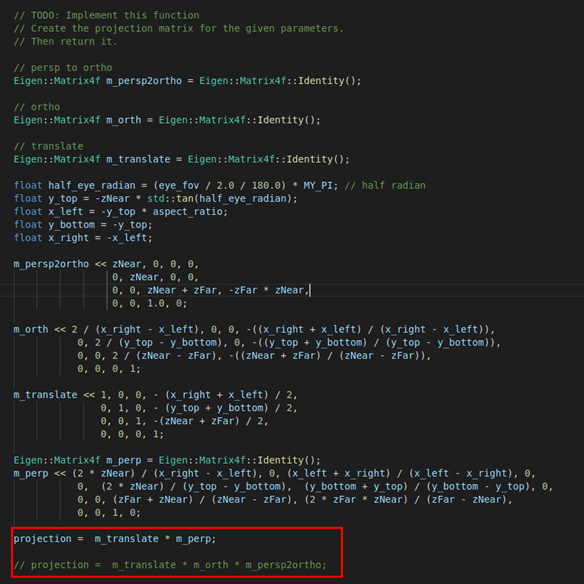
注：translate 是将中心点移到原点
————————————————————（补充）————————————————————————
#透视矩阵的推导
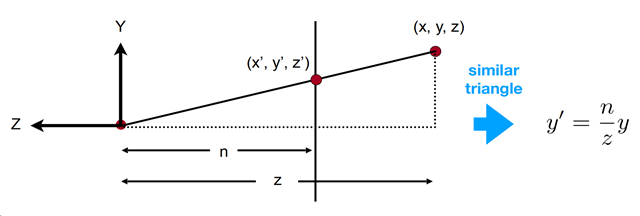
sin(θ) = y / z = y’ / n
y’ = (y/z) * n = ny / z
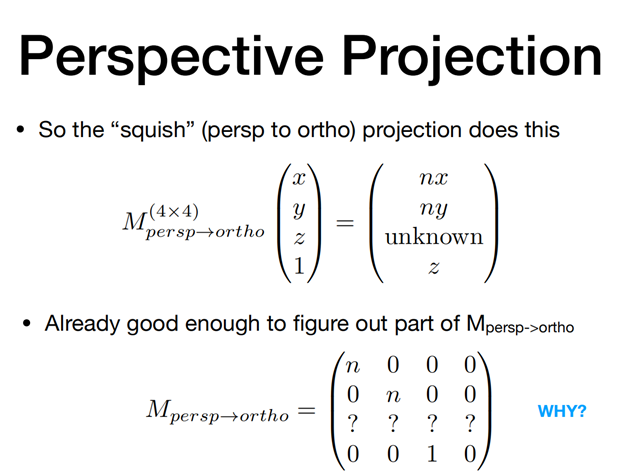
如何求 透视 到 正交投影的矩阵（上图所示的？）
数学含义就是一个点（x，y，z）经过一个矩阵变换后变成了（x’， y’， z’），求这个矩阵，其中 x’ = nx / z，y’ = ny / z
何求？？？？（0 0 A B）呢，分别用二个特殊的点进行替代 z 点，（x, y, n）与（x, y, f）
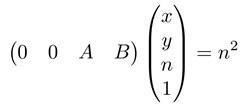
已经 n、f 求 A、B的值，便可得到 A = n + f，B = -nf，得到最终的透视矩阵
