二叉查找树和笛卡尔树

目录

• 二叉查找树
  • 定义
  • 作用
  • 操作
    • 查找
    • 插入
    • 删除
  • 缺点
• 笛卡尔树
  • 定义
  • 操作
    • 构造

1|0二叉查找树

1|1定义

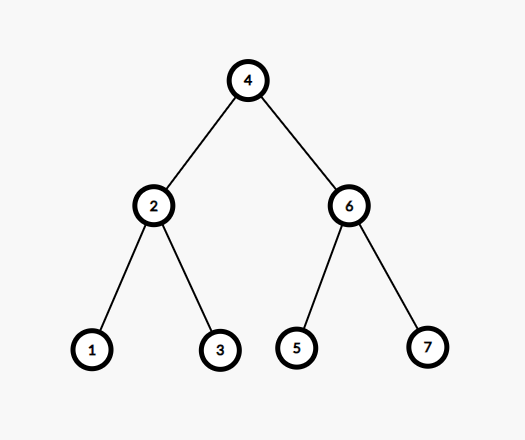
​ 二叉查找树（Binary Search Tree，BST），又名二叉搜索树或二叉排序树。

​ 它是一类特殊规定的二叉树，它应当满足以下条件：

1. 每个节点有唯一确定的权值
2. 非叶子节点的权值比其左子树中所有节点权值大
3. 非叶子节点的权值比其右子树中所有节点权值小

​ 由于上述特性，易知BST的中序遍历是一个有序排列。

​ 特别地，空树也是一棵BST（觉得有意思就记下来了？）

1|2作用

​ 顾名思义，它用于快速地查找数据，同时它也支持快速地插入与删除数据。

​ 因为在BST上查找一个数，所需的查找次数不超过树的深度。查找过程类似于二分，运气好的话，它的时间复杂度能和二分相同。

​ 实际上，由于原序列本身无序，所以每次查找的时间复杂度会在$O(\log n)$到$O(n)$之间浮动。（具体原因后面再写）

1|3操作

查找

​ 通过递归实现。

​ 二分思想中，每一次会在区间[l,r]中取mid，将区间均分为两半。并对mid进行检查，以此决定接下来是查找左区间还是右区间。

（说起来，初中数学有教过二分吧？）

​ 对应的，在BST中，当前查找到的节点相当于区间的mid，将区间分为左子树和右子树两部分（遗憾的是，并非均分）。对当前节点进行“判断”，就可以决定接下来的查找范围是枣子树还是柚子树。

​ （好耶，是枣子柚子二选一！）

​ （试图把左子树称为枣子树，把右子树称为柚子树）

插入

​ 在查找操作的基础上加一点点东西。

​ 如果按照给定顺序和值（即给定序列）插入，最终建成的BST一定是唯一的。

​ 对于需要插入的数据，我们可以通过查找得到它“应该在的位置”。如果这个位置是空位，就在这个位置插入新节点。

（如果不是空位，说明之前已经有同样的数据，可以按照需要进行记录。例如在每个节点用int cnt记录数据出现次数）

删除

​ 有删除操作时，BST可能不唯一。

​ 好在有两种轻松愉悦的情况：

​ 1.如果要删除的节点孤苦伶仃，无儿无女，无依无靠，那直接把它删了就行，反正也没节点给它收尸不是吗。

​ 2.如果要删除的节点只有枣子树或只有柚子树（总之就是只有一个儿子），那么直接删除它，并将子树衔接上来，代替它的位置。

​ 其余情况比较麻烦（儿孙们要争夺祖父的地位（？））

​ 这里列举两种常见的解决方法，同样是递归操作：

​ 其一是：用左子树中的最大节点，顶替删除节点。但是对于左子树来说，这相当于删除了“最大节点”，所以继续递归，直到前面两种情况之一。

​ 其二是：用右子树中的最小节点，顶替删除节点。同理，继续递归。

​ 由于删除时的操作，BST可能变成奇奇怪怪的形状。

1|4缺点

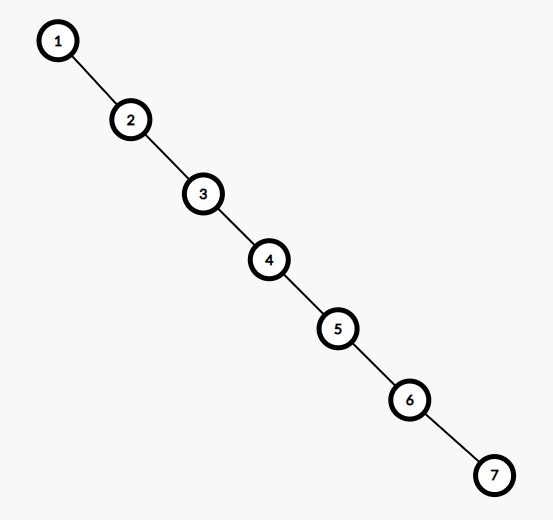
​ 形态不稳定。

​ 前面有说过，它每次操作的时间复杂度最好是$O(\log n)$，最差会到$O(n)$。这是因为插入序列的顺序不一定，按照它建出的BST可能恰好平衡，也可能退化成一条链。

​ 比如序列4213657是一棵满二叉树：

​ 而序列1234567就会退化成一条链：

​ 此外，在删除的过程中，还会改变树的形态，也可能会使它退化。

​ BST存在的问题即“如何保持平衡的形态”。后续的替罪羊树、Treap树、Splay树、红黑树等等都是基于“维护平衡”这一问题的BST树优化算法。

2|0笛卡尔树

2|1定义

笛卡尔树是一类特殊的二叉查找树，其和一般BST的区别在于每个节点包括两个权值信息。

一棵笛卡尔树应当满足如下条件：

1. 每个节点包括两个唯一确定的权值$(x_u,y_u)$
2. 只考虑权值$x_u$的情况下，树的形态应当符合一棵二叉查找树的性质。
3. 只考虑权值$y_u$的情况下，树的形态应当符合大根堆或小根堆的性质。

根据OI Wiki的说明，如果一棵笛卡尔树的$(x_u,y_u)$唯一确定，那么这棵笛卡尔树的形态唯一。

关于唯一确定：即$(x_u,y_u)$均已知，且$x_u$互不相同，$y_u$互不相同。

2|2操作

构造

首先将节点按照$x_u$从小到大的顺序排序，现在假设我们要构造的笛卡尔树符合小根堆的性质。

由于二叉查找树的性质，且$x_u$递增，显然新节点的位置应该尽可能靠右。可以通过维护从根开始的一条极长链，满足每个节点都是其父节点的右儿子。

这条链满足链上节点的权值$x,y$均单调递增，可以看作一个单调栈，或者说可以用单调栈来维护。加入新节点$u$的时候，在链上找到深度最大的节点$v$满足$y_v<y_u$，将其作为$u$的父节点。显然$x_u>x_v$，故令$u$为$v$的右儿子。

如果$v$有右儿子，则将$v$的右子树拆下来，接在$u$的左子树下。由于$v$是深度最大的$y<y_u$，所以$y_v<y_u<y_{rs(v)}$，且$x_u>x_{rs(v)}$，所以这样操作不会破坏笛卡尔树的性质。

以洛谷P5854【模板】笛卡尔树为例，代码如下：

#include <bits/stdc++.h>
using namespace std;
#define lld long long

const int N = 1e7+5;
int n, q[N], tl = 0;
struct Tree{
  int val, ls, rs;
}t[N];

void read(int &x){
  char input = getchar(); x = 0;
  while(input<'0'||input>'9')
  	input = getchar();
  while(input>='0'&&input<='9'){
  	x = x*10+(input-'0');
  	input = getchar();
  }
}

int main(){
  scanf("%d", &n);
  for(int i = 1; i <= n; i++){
  	int T = tl; read(t[i].val);
  	while(tl && t[q[tl]].val > t[i].val) tl--;
  	if(tl) t[q[tl]].rs = i;
  	if(tl < T) t[i].ls = q[tl+1];
  	q[++tl] = i;
  }
  lld ans1 = 0, ans2 = 0;
  for(int i = 1; i <= n; i++){
  	ans1 ^= (lld)i*(t[i].ls+1);
  	ans2 ^= (lld)i*(t[i].rs+1);
  } printf("%lld %lld\n", ans1, ans2);
  return 0;
} // 此题的恶心之处在于必须快读

__EOF__

本文作者：Meteor2008
本文链接：https://www.cnblogs.com/meteor2008/p/18474364.html
关于博主：评论和私信会在第一时间回复。或者直接私信我。
版权声明：本博客所有文章除特别声明外，均采用 BY-NC-SA 许可协议。转载请注明出处！
声援博主：如果您觉得文章对您有帮助，可以点击文章右下角【推荐】一下。您的鼓励是博主的最大动力！