论文笔记 - Fantastically Ordered Prompts and Where to Find Them: Overcoming Few-Shot Prompt Order Sensitivity
prompt 的影响因素
Motivation
- Prompt 中 Example 的排列顺序对模型性能有较大影响(即使已经校准参见好的情况下,选取不同的排列顺序依然会有很大的方差):
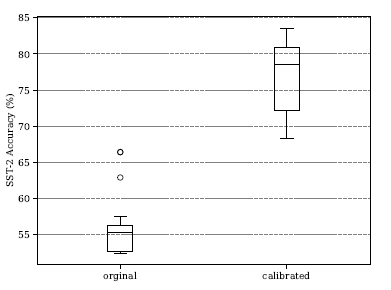
- 校准可以大幅度提高准确率,但是不同的排列顺序方差依然很大
Analysis
- 提出探测集(probing set),流程如下:
- 训练集 $S={(x_i, y_i)}$,模板转换函数(将一组数据转换为自然语言) $t_i=\tau (x_i,y_i)=input:x_i,type:y_y$,因此自然语言数据集 $S'=\{t_i\}$;
- 排列方程集合 $\mathfrak{F}=\{f_m\},m=1\rightarrow n!$,$f_m(S')=c_m$ 为一种训练数据的组合顺序($m=1\rightarrow n!$);
- 对于每一种排列组合$c_m$,使用语言模型进行去预测后续的句子(注意这里没有加上测试集的问题,纯粹对训练集进行组合),得到模型生成的新的 example:$g_m\propto P(...|c_m;\theta)$,$\theta$为语言模型的参数,对生成序列解析得到模型生成的数据集:$D=\{\tau ^{-1}(g_m)\},m=1\rightarrow n!$。
- 针对探测集提出两种评估 prompt 的指标:
-
Global Entropy
- 对探测集合中探测数据$(x'_i, y'_i)\in D$(生成的 label 不需要,不具有参考意义),选择一种排列组合(上下文)$c_m$进行推理得到$\hat{y_{i,m}}$,即:
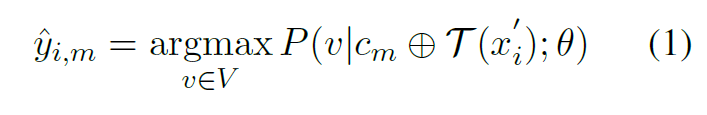
- 对探测集中的每个探测数据进行预测,求得每个预测的种类占探测集的比例:
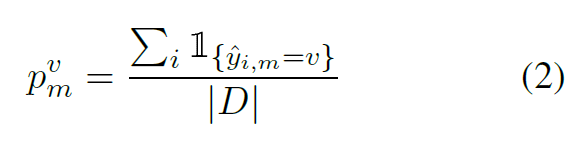
- 最后求熵(熵反应了预测各个种类的均匀程度,预测的正确与否并不重要,假如熵非常小,说明预测的结果 bias 非常大):
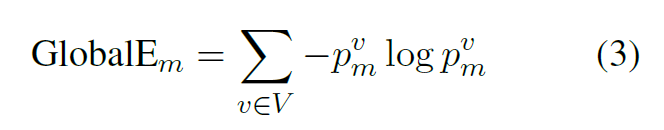
-
Local Entropy
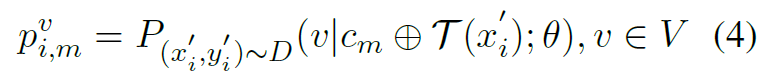
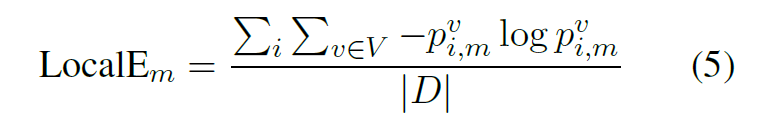
- 与全局熵类似,只不过先求熵再求和。
-
为什么上面的方法有用呢?
- 个人猜想:你能得到的训练集是非常有限的,假设改变 example 的排列顺序会使 output distribution 发生改变。假如你只有 4 个 example,那么你最多能模拟出来 24 种不同的 distribution(很多模拟不出来但是没有办法,受数据制约),也就是说你得到的包含 24 个数据的探测集其实就是尽最大能力准备出来的多样数据集。如果在这些探测数据上,某个排序$c_m$预测的结果集合很均匀(各种类别数量差不多),那么说明这种排序 rebust 比较强(这种排序没有倾向性,导致生成的问题都是中性的,生成什么label的可能性都一样)。


