动手动脑2----线性同余产生1000个随机数
来自百科上的介绍:
线性同余方法(LCG)是个产生伪随机数的方法。
它是根据递归公式:
其中 是产生器设定的常数。
是产生器设定的常数。
LCG的周期最大为 ,但大部分情况都会少于M。要令LCG达到最大周期,应符合以下条件:
,但大部分情况都会少于M。要令LCG达到最大周期,应符合以下条件:
线性同余算法有m 、a 、c 和X0 4个参数,通过置Xn + 1 ≡aXn + c (mod m) ,求得随机数序列< Xn > , 这个序列称作线性同余序列。m、a 、c 和X0 分别称做模数、乘数、增量和初始值。线性同余方法速度快,如果对乘数和模数进行适当的选择,可以满足用于评价一个随机数产生器的3 种准则:
1.这个函数应该是一个完整周期的产生函数。也就是说,这个函数应该在重复之前产生出0 到m之间的所有数;
2.产生的序列应该看起来是随机的;
3.这个函数应该用32bit 算术高效实现。
在我的实现中,X0(或者叫N0)用系统提供的时间,A选16087,B选取0,M选取2147483647,即1<<31-1
源代码:
1 public class Test2 { 2 public static void random(int num) { 3 long send = System.currentTimeMillis(); 4 for(int i = 1;i<=num;++i) { 5 send = (send*16807+0)%((1<<31) - 1); 6 System.out.print(send+" "); 7 if(i % 10 == 0)System.out.println(); 8 } 9 } 10 public static void main(String[]args) { 11 Test2.random(1000); 12 } 13 }
验证截图:

(直接截取了一部分)

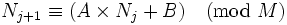
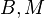
 ;
;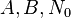 都比
都比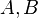 是正整数。
是正整数。
 浙公网安备 33010602011771号
浙公网安备 33010602011771号