课程作业----递归那些事

递归的三个小题

（1）杨辉三角的那些事儿

以下为从度娘上复制的内容:

1

1 1

1 2 1

1 3 3 1

1 4 6 4 1

.。。。。。。。。

观察后可知:

 1. 每行数值左右对称，且均为正整数。

     2. 行数递增时，列数亦递增。

     3. 除斜边上的1外，其余数值均等于其肩部两数之和。

     杨辉三角与二项式定理有密切关系，即杨辉三角的第n行(n=0…MAX_ROW)对应二项式(a+b)ⁿ展开(Binomial Expansion)的系数集合。例如，第二行的数值1-2-1为幂指数为2的二项式(a+b)²展开形式a² + 2ab + b²的系数，即。

     应用组合公式可推导出杨辉三角的特征1和3，如下：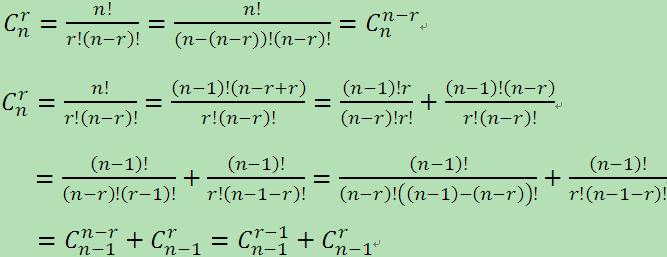

 

根据上面的有关组合数和二项式定理的内容，以及递推关系，利用递归的思想提供三个输出有限行杨辉三角的方法:

(i)直接使用C(r,n),设计思想很简单就是2层嵌套的for循环语句，利用组合数公式分别计算每个位置上的数字。当然组合数公式是直接多次调用提前写好的计算阶乘的方法来算。这个计算阶乘的方法就是利用了递归的操作。

简单的展示下递归的流程图吧，双循环的流程图没啥可画的。

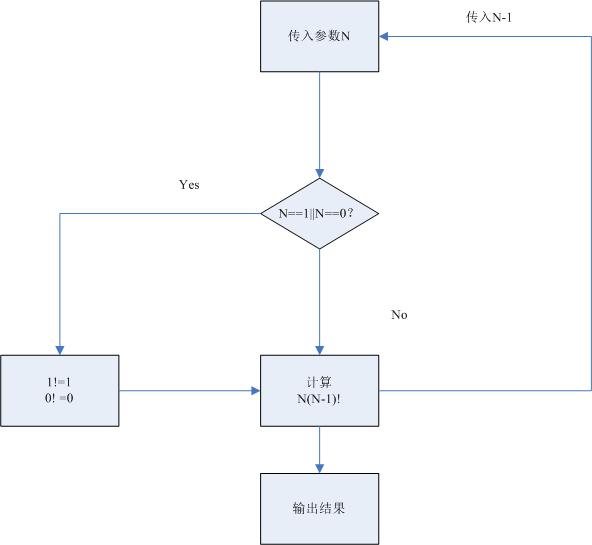
(这个图很难说时正确的，只是个简单的流程图，基本上递归都是伪代码来表示)

class PaTri1{
        public static BigInteger calculateN2(int n) {  //防止数据过大，用大整数表示
        if(n==1 || n==0){
            return BigInteger.valueOf(1);
        }
        return BigInteger.valueOf(n).multiply(calculateN2((n-1)));
    }
    public static void Ptriangle1(int row) {
        for(int i = 0;i<row;i++) {
            for(int j = 0;j<=i;++j) {
                System.out.print(PaTri1.calculateN2(i).divide(PaTri1.calculateN2(j).multiply(PaTri1.calculateN2(i - j)))+" ");
            }    //组合数公式，直接调用静态方法calculateN2()
            System.out.println();
        }
    }
}

 在主函数中直接调用PaTri1.Ptriangle1()这个静态方法即可

（ii）换个更加简单一点的方法，这次不用递归，用递推

即C(r,n) = C(r-1,n-1)+C(r,n-1)这个公式，不再使用那个阶乘的公式，直接从最顶上开始往下推，只不过要记录每个已经计算出来的值，以便后面的方便使用。

设计思路:还是那两层嵌套的for循环，自顶向下，从第一个位置算起，利用最上面那第三条规律，即该位置的数值等于它两肩上的两数之和(这里实在没必要再用那个组合数公式了)，如果它上面只有一个数，剩下一个用0补。

class PaTri2{
    private BigInteger[][]tmp;//用来记录已经计算了的值
    public BigInteger Cnr(int r,int n) {
        if(r<0)return BigInteger.valueOf(0);    //前两行就属于上面说的肩上为0的数
        else if(r > n)return BigInteger.valueOf(0);  
        else return tmp[r][n];  //其他情况一定是有值存在的，因为是计算一个记录一个值，由于后面的数值计算要用到前面的值，而前面的值已经储存起来了，所以直接返回
    }
    public void Ptriangle2(int row) {
        tmp = new BigInteger[row][row];
        tmp[0][0] = BigInteger.valueOf(1);
        System.out.println(Cnr(0,0));
        for(int i = 1;i<row;++i) {
            for(int j = 0;j<=i;++j) {
                tmp[j][i] = Cnr(j-1,i-1).add(Cnr(j,i-1));//连续地调用，不会发生递归，一次出结果
                System.out.print(tmp[j][i]+" ");
            }
            System.out.println();
        }
    }

使用这个类需要定义对象，通过对象实例调用成员方法传值进行指定行杨辉三角的输出 

（iii）换种递归方式来写，第一种方法的递归体现在具体的每个位置数值的计算上，第二种和递归无关是多次利用递推公式来自顶向下计算。这种方法则和第二种方法完全相反，是自底向上的递归，从最后一行第一个位置开始(只计算最后一行)，每一个数字都需要它肩上两个数字，返回这些数字值的是一个方法，由此通过递归的调用这些方法来完成上面的数字的计算，看似是先从最后往上，实则是还是先计算最前面的，依次往后带入前面已知的结果进行计算。

class PaTri3{
    private BigInteger[][]crn;        //用来记录每个已经计算出来的位置上的数值
    public BigInteger Cnr(int r,int n) {
        if(r == 0&&n == 0) {     //最顶上的出口
            crn[r][n] = BigInteger.valueOf(1);
            return BigInteger.valueOf(1);
        }
        else if(r <0)return BigInteger.valueOf(0); //越界的应该为0的值，有些边界上的数肩上只有一个数字，另一个不存在的用0来替代，这里就是为那些肩上只有一个数的位置的计算是发生的调用作准备
        else if(r > n)return BigInteger.valueOf(0); //同上
        else {
            crn[r][n] = Cnr(r-1,n-1).add(Cnr(r,n-1));  //利用了递推公式进行递归调用，并将结果保留在相应的位置上
            return crn[r][n];
        }
    }
    public void Ptriangle3(int row) {
        crn = new BigInteger[row][row]; 
        for(int j = 0;j<=row - 1;j++)
                Cnr(j,row - 1);     //直接计算最后一排位置上的数字，间接通过该函数内部的递归计算所有位置上的数字
        for(int i = 0;i<row;++i) {         //用双层for循环打印保存的结果
            for(int j = 0;j<=i;++j)
                System.out.print(crn[j][i]+" ");
            System.out.println();         //分行输出
        }
    }
}

 （这个类写的比较差，不能在计算的同时输出相应位置上的计算结果，而且很多位置会重复计算。在每个位置上可以设置相应的标记值，标记值正确则直接取已经保存了的计算结果，标记值错误则调用方法计算，但是这样会额外占据很多空间，还有就是可以只计算每行前一半位置上的不重复的数字，在输出时对循环条件加以限制可以将剩下那一半重复了的输出出来。这两个思路都能在一定程度上解决计算步骤过多的问题:前一种能完全解决重复计算的问题，后一种只是减少了近一半的运算量，剩下的一半还需要进行和前一种思路相同的操作才能取消重复的运算）使用时同样需要定义对象实例，通过具体的对象实例调用成员方法。

插张验证的截图:

 

(2)汉诺塔

汉诺塔是个古老的问题，就是A柱上串着从大到小一次摆放的盘子，这摞盘子以相同的形式摆放在另一个C柱上，一次只能移动一个盘子，且在放置盘子的过程中大盘在下小盘在上，有一个空的B柱做过度，来回移动盘子的问题，让你给出移动的步骤。

这个问题可以递归也可以不递归，这里就写下递归解决的思路。首先要有方法move(char a,char b),表示从柱子a移动到柱子b的过程。其次就是Hanoi(int num,char a,char b,char c)方法的完成，问题的解决就是重复递归调用这个Hanoi方法。我们要清楚，当只有一个盘子的时候，直接把这个盘子从a移动到c即可，也就是num = 1时，直接执行move(a,c);不过当有两个盘子的时候，要先将小盘子放到b上，然后就是只有一个盘子的情况了，也就是把最后一个盘子直接从a移动到c，最后再将b上的盘子移动到c即可；但是有三个盘子或者以上的时候情况会复杂一些，你需要把除了最底下那个最大盘子外所有的盘子看成一个盘子，把这一整个盘子先移动到c柱。一下子就移动到b显然不可能，不过你会发现，这个时候c柱子是空的，也就是说把n个盘子以b为过度从a移动到c的过程其实和把n - 1个盘子以c为过度从a移动到b是同一个过程，这就是递归的来源了，问题的子问题需要和原来问题一样的解决方式，只是再规模上缩小了一些。回头再看两个盘子的情况，将上面小盘子从a移动到b也是这么个步骤，故n>=2时，都是需要把n-1个盘子以c为过度从a移动到b的过程的(注:这里也要注意三个柱子的角色问题，初始状态下a柱是起始柱，c柱是目标柱，空着的b柱是一个辅助的柱子，但是再移动过程中这三个柱子的角色会变化，比如第二部移动那n - 1个盘子的时候，整个过程是以a柱是起始柱，b柱是目标柱，空着的c柱才是用来辅助移动的柱子，等到了n-1的子问题n-2时，三个柱子的角色又不相同了，所以不能被已经固定的a,b,c三个柱子迷惑，因为他们的角色在解决问题的不同阶段不一定是一样的，直接点讲，在调用Hanoi过程中重要的是传入a,b,c的顺序)。现在假设n - 1个盘子已经按要求移动到b柱上了，直接将剩下的最大盘子从a移动到c即可，最后，还是一样的操作，以空着的a柱作为辅助移动的柱子，将放在b上的n - 1盘子移动到c柱上。画成流程图很简单

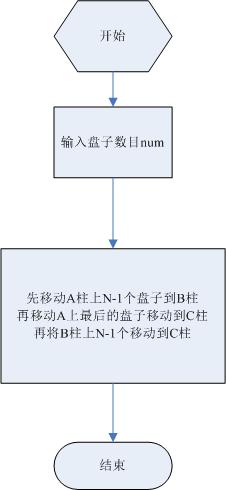
源码比较简单:

public class Hanoi {
      public static int round = 0;
      public static void move(char a,char b) {
          System.out.println("第"+(++round)+"步:"+a+"----->"+b);
      }
      public static void hanoi(int num,char a,char b,char c) {
          if(num<=0) {
              System.out.println("不能进行汉诺塔游戏!");
              return;
          }
          if(num == 1)move(a,c);
          else {
              hanoi(num - 1,a,c,b);
              move(a,c);
              hanoi(num - 1,b,c,a);
          }
      }
      public static void main(String[]args) {
          Scanner s = new Scanner(System.in);
          System.out.print("输入盘子的个数:");
          int num = s.nextInt();
          s.close();
          System.out.println("开始步骤分解:");
          Hanoi.hanoi(num, 'A', 'B', 'C');
          return;
      }
}

 

（3）回文

不多介绍了，直接上思路：判断一个字符串是不是回文，首先要看他的第一个和最后一个字符是否相同，不相同直接pass掉，相同则缩短该字符串检索范围，忽略首位字符后看新的首尾字符是否相同，以此类推。很明显的能看出递归。递归的出口有两个:当字符串长度为基数时，递归到最后只有一个字符；当字符串长度为偶数时，递归到最后有相邻的两个字符，如果这两个字符相同则是回文。

流程图:

源代码:

public class Palindrome {
      public static void isPal(String str,int low,int high) {
          if(low==high) {
              System.out.println(str+"是回文");
              return;
          }
          if(low == high - 1) {
              if(str.charAt(low)==str.charAt(high)) {
                  System.out.println(str+"是回文");
                  return;
              }
              else {
                  System.out.println(str+"不是回文");
                  return;
              }
          }
          if(low == high - 2) {
              if(str.charAt(low)==str.charAt(high)) {
                  System.out.println(str+"是回文");
                  return;
              }
              else {
                  System.out.println(str+"不是回文");
                  return;
              }
          }
          if(low<high&&high-low>2) {
              if(str.charAt(low)==str.charAt(high))isPal(str,low+1,high-1);
              else {
                  System.out.println(str+"不是回文");
                  return;
              }
          }
      }
      public static void main(String[]args) {
             System.out.print("输入一个字符串:");
             Scanner s = new Scanner(System.in);
             String str = "";
             str = s.next();
             s.close();
             Palindrome.isPal(str,0,str.length()-1);
      }
}