OpenMP学习 第四章 线程与OpenMP编程模型
第四章 线程与OpenMP编程模型
编译器指令
为了将顺序程序转换为并行程序,修改代码的最小干扰方式是通过编译器指令.
在C/C++中,指令通过编译器表示
#pragma omp parallel[clause[[,]clause]...]
#pragma omp parallel private(x)
{
//code executed by each thread
}
大部分OpenMP指令适用于代码块.
概括代码: 编译器在编译过程中用程序中的一些语句创建函数.编译器在编译过程创建函数,并在其生成的代码中调用该函数.
结构化块: 与指令相关联的代码块中的代码所形成的代码块.
由于有时多重嵌套结构化块的存在,在OpenMP中,存在一种常见的做法: 在收尾大括号处添加注释,以指定它与哪个OpenMP pragma绑定.
#pragma omp parallel
{
//..do lots of stuff
}//end of parallel region
构造: 指令与结构化块的组合.
词汇范围(lexical extent): 编译单元包含指令的可见代码.其为静态的,是你在包含指令的源代码中看到的东西.
区域(region): 与构造相关联的线程所执行的所有代码.区域是"动态范围",在程序运行前,不知道内部执行了哪些代码.
为了学习OpenMP,你只需要掌握OpenMP规范中的一些元素:
- 编译器指令
- 运行时库例程
- 环境变量
使用OpenMP
本节主要涉及到的例程:
- 通过库例程显式改变默认值的例程:
void omp_set_num_threads(int num_threads);
- 返回线程序号的库例程(返回值为线程数-1)
int omp_get_thread_num();
- 返回当前线程组内有多少线程的库例程
int omp_get_num_threads();
- 从过去某一时刻返回以秒为单位的时间的例程
double omp_get_wtime();
fork-join模式: 使用parallel指令创建一个线程集合(即线程组),在构造结束时,线程组被销毁,只留有一个线程.
程序以一个初始线程开始,当该线程遇到有利于并行的代码时,就会 fork(分叉) 出一个线程组来执行这个并行区域的代码.我们称线程组的初始线程为"主线程".完成后,线程组 合并(join) 在一起.
栅栏(barrier): 栅栏是程序中的一个点,在任何线程继续之前,线程组中的所有线程都必须到达这个点.
一个程序开始时,在创建线程组的时候会有一个特定的默认线程数.OpenMP实现在选择这个数字时的灵活性.
一个线程组一旦形成,那么其规模就是固定的.OpenMP运行时系统一旦启动,就不会减少线程组的规模.
数据环境与线程交互的模式: 在并行构造之前声明的变量在线程之间共享,而在并行构造内部声明的变量是线程的私有变量.
但是有一点需要注意:在结构化块内部声明的静态变量依然对全体线程可见.
我们通过下面一个实验来说明:
#include <iostream>
#include <omp.h>
#include <vector>
import <format>;
void pooh(int ID,double* A,std::vector<int>&IDs)
{
A[ID] = ID;
IDs.push_back(ID);
}
int main()
{
double A[10] = { 0 };
std::vector<int>IDs;
omp_set_num_threads(4);
#pragma omp parallel
{
static int temp = 0;
temp++;
int ID = omp_get_thread_num();
pooh(ID, A, IDs);
printf("A of ID(\%d)=\%lf\nand temp is (\%d)\n", ID, A[ID], temp);
}//end of the parallel
for (auto iter : IDs)
std::cout << std::format("ID:{}", iter) << std::endl;
return 0;
}
在这里,思考一个问题:如果你想知道在并行区域完成合并而且不再存在后并行区域内部曾使用过的线程数怎么办?
答案是: 在并行区域前声明一个变量,使其变成共享变量.
注意:在对该共享变量进行读写时,需要注意数据竞争带来的未定义行为.
SPMD设计模式
单指令多数据设计模式(SPMD):
- 启动两个或多个执行相同代码的线程
- 每个线程确定其ID和线程组中的线程数
- 根据ID和线程组中的线程数在线程之间分配工作
循环迭代的按周期分布划分: 首先对循环进行分割,分割后考虑数据竞争问题的处理.需要对局部变量与私有变量进行划分.
ID = omp_get_thread_num();
numthreads = omp_get_num_threads();
for(int i = ID;i<num_steps;i=i+numthreads)
//body of loop
经验法则:一旦出现对私有变量存储的需要,便使用数组.
基于循环的块状分解: 在线程间分配循环工作,给每个线程一个大小近似相等的循环迭代块,将最后一个线程(ID=numthreads-1)所负责块的最后一个迭代索引设置为总步数.
ID = omp_get_thread_num();
numthreads = omp_get_num_threads();
istart = ID*numsteps/numthreads;
iend = (ID+1)*numsteps/numthreads;
if(ID==(numthreads-1))
iend = num_steps;
for(int i = istart;i<iend;i++)
//body of loop
并行数值积分
问题描述: 数学上,我们已经知道了:
$$\int\limits1_0\dfrac{4.0}{(1+x2)}dx=\pi$$
为了对其进行计算,将积分近似为多个矩形面积的和:
$$\sum\limits^N_{i=0}F(x_i)\Delta x\approx\pi$$
于是,现在需要设计一个并行算法对其进行解决.
- 非并行解法:
下面是一种正常对其进行计算的解法,利用中点规则对值进行估计:
#include <iostream>
#include <omp.h>
import <format>;
static long num_steps = 100000000;
double step;
int main()
{
double x, pi, sum = 0.0;
double start_time, run_time;
step = 1.0 / (double)num_steps;
start_time = omp_get_wtime();
for (int i = 0; i < num_steps; i++) {
x = (i + 0.5) * step;
sum += 4.0 / (1.0 + x * x);
}
pi = step * sum;
run_time = omp_get_wtime() - start_time;
std::cout << std::format("pi={},{} steps,{} secs\n",
pi,
num_steps,
run_time
);
}
得到结果:
pi=3.1415926535904264 in 1.0227031000249553 secs
- 按周期分布划分循环迭代的SPMD并行数值积分:
- 不同步长情况
#include <iostream>
#include <omp.h>
#include <fstream>
#include <cmath>
import <format>;
#define TURNS 100
#define PI 3.141592653589793
long double num_steps = 1e9;
double step;
int main()
{
std::ofstream out;
out.open("example.csv", std::ios::ate);
out << "NTHREADS,pi,err,run_time,num_steps" << std::endl;
int NTHREADS = 10;
double sum[TURNS] = { 0,0 };
for (int j = 1; j < TURNS; j++) {
double start_time, run_time;
double pi, err;
pi = 0.0;
memset(sum, 0.0, sizeof(double)*NTHREADS);
int actual_nthreads;
step = 1.0 / (double)num_steps;
omp_set_num_threads(NTHREADS);
start_time = omp_get_wtime();
#pragma omp parallel
{
int id = omp_get_thread_num();
int numthreads = omp_get_num_threads();
double x;
if (id == 0)
actual_nthreads = numthreads;
for (int i = id; i < num_steps; i += numthreads) {
x = (i + 0.5) * step;
sum[id] += 4.0 / (1.0 + x * x);
}
}//end of parallel
pi = 0.0;
for (int i = 0; i < actual_nthreads; i++)
pi += sum[i];
pi = step * pi;
err = pi - PI;
run_time = omp_get_wtime() - start_time;
std::cout << std::format("pi is {} in {} seconds {} thrds.step is {},err is {}",
pi,
run_time,
actual_nthreads,
step,
err
)<<std::endl;
out << std::format("{},{:.15f},{:.15f},{:.15f},{}",
NTHREADS,
pi,
err,
run_time,
num_steps
) << std::endl;
num_steps /= 2.0;
}
out.close();
return 0;
}
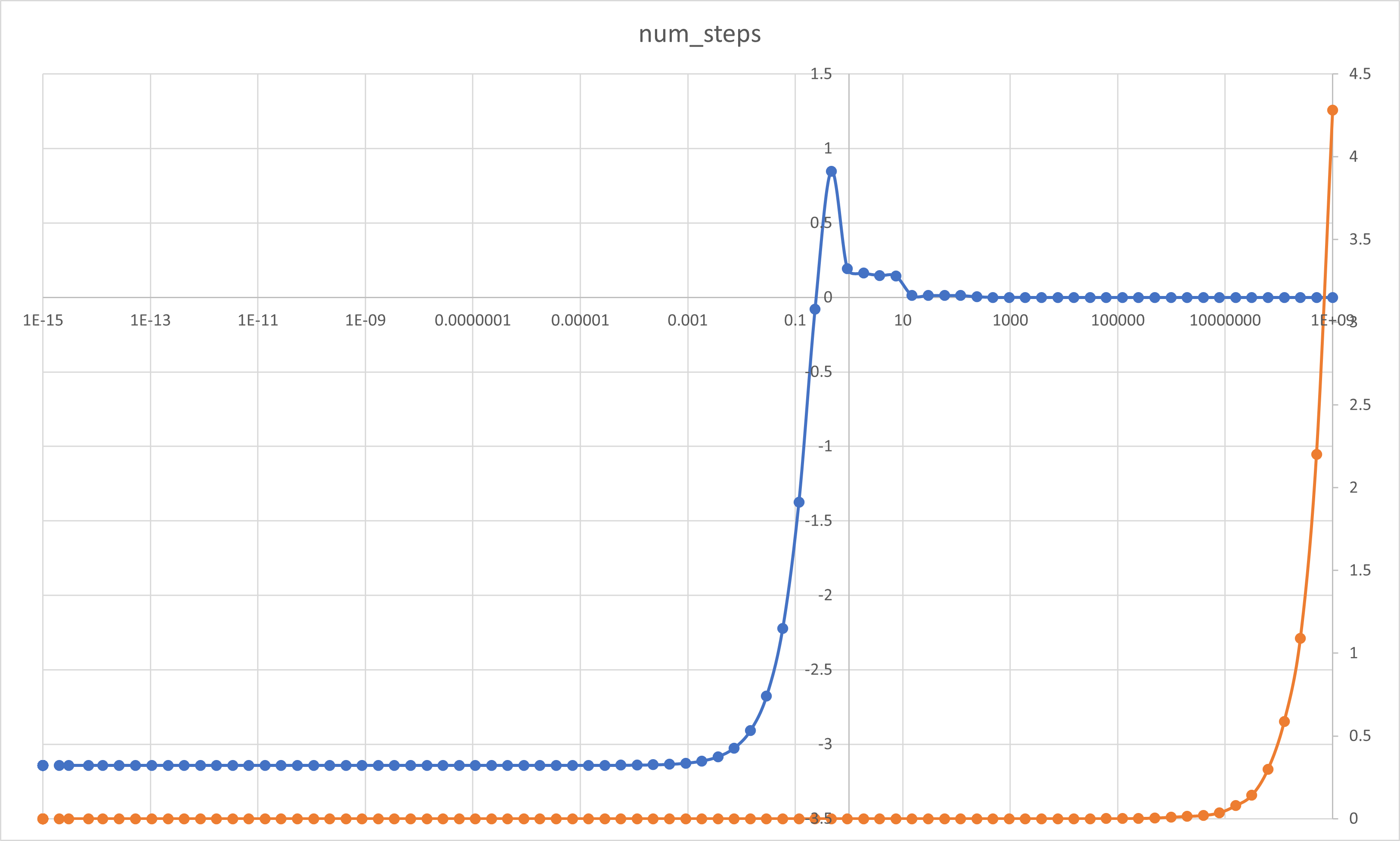
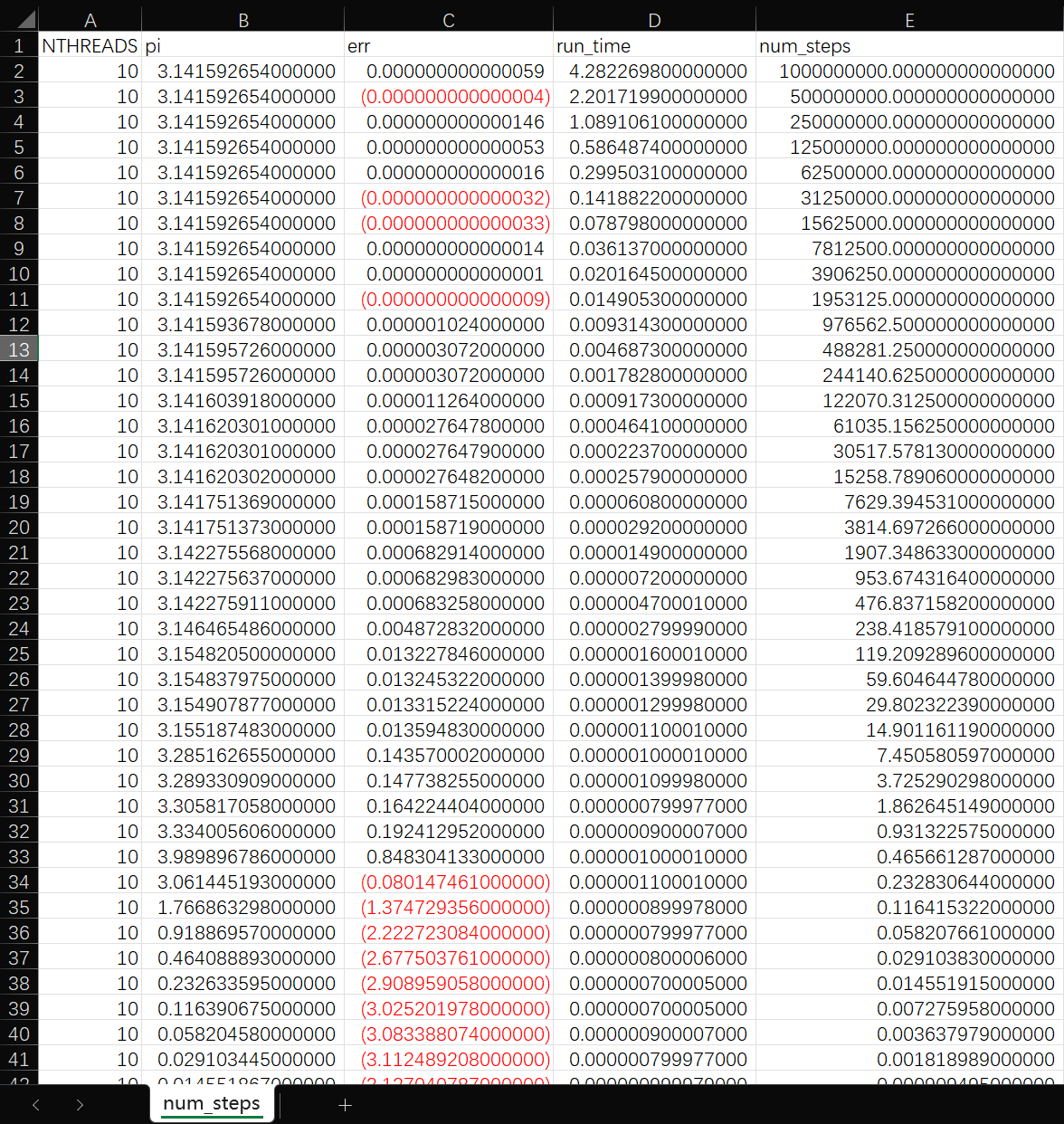
- 不同线程数情况
#include <iostream>
#include <omp.h>
#include <fstream>
import <format>;
#define TURNS 100
#define PI 3.141592653589793
long double num_steps = 1e8;
double step;
int main()
{
std::ofstream out;
out.open("example.csv", std::ios::ate);
out << "NTHREADS,pi,err,run_time,num_steps" << std::endl;
double sum[TURNS] = { 0,0 };
for (int NTHREADS = 1; NTHREADS < TURNS; NTHREADS++) {
double start_time, run_time;
double pi, err;
pi = 0.0;
memset(sum, 0.0, sizeof(double)*NTHREADS);
int actual_nthreads;
step = 1.0 / (double)num_steps;
omp_set_num_threads(NTHREADS);
start_time = omp_get_wtime();
#pragma omp parallel
{
int id = omp_get_thread_num();
int numthreads = omp_get_num_threads();
double x;
if (id == 0)
actual_nthreads = numthreads;
for (int i = id; i < num_steps; i += numthreads) {
x = (i + 0.5) * step;
sum[id] += 4.0 / (1.0 + x * x);
}
}//end of parallel
pi = 0.0;
for (int i = 0; i < actual_nthreads; i++)
pi += sum[i];
pi = step * pi;
err = pi - PI;
run_time = omp_get_wtime() - start_time;
std::cout << std::format("pi is {} in {} seconds {} thrds.step is {},err is {}",
pi,
run_time,
actual_nthreads,
step,
err
)<<std::endl;
out << std::format("{},{:.15f},{:.15f},{:.15f},{}",
NTHREADS,
pi,
err,
run_time,
num_steps
) << std::endl;
}
out.close();
return 0;
}
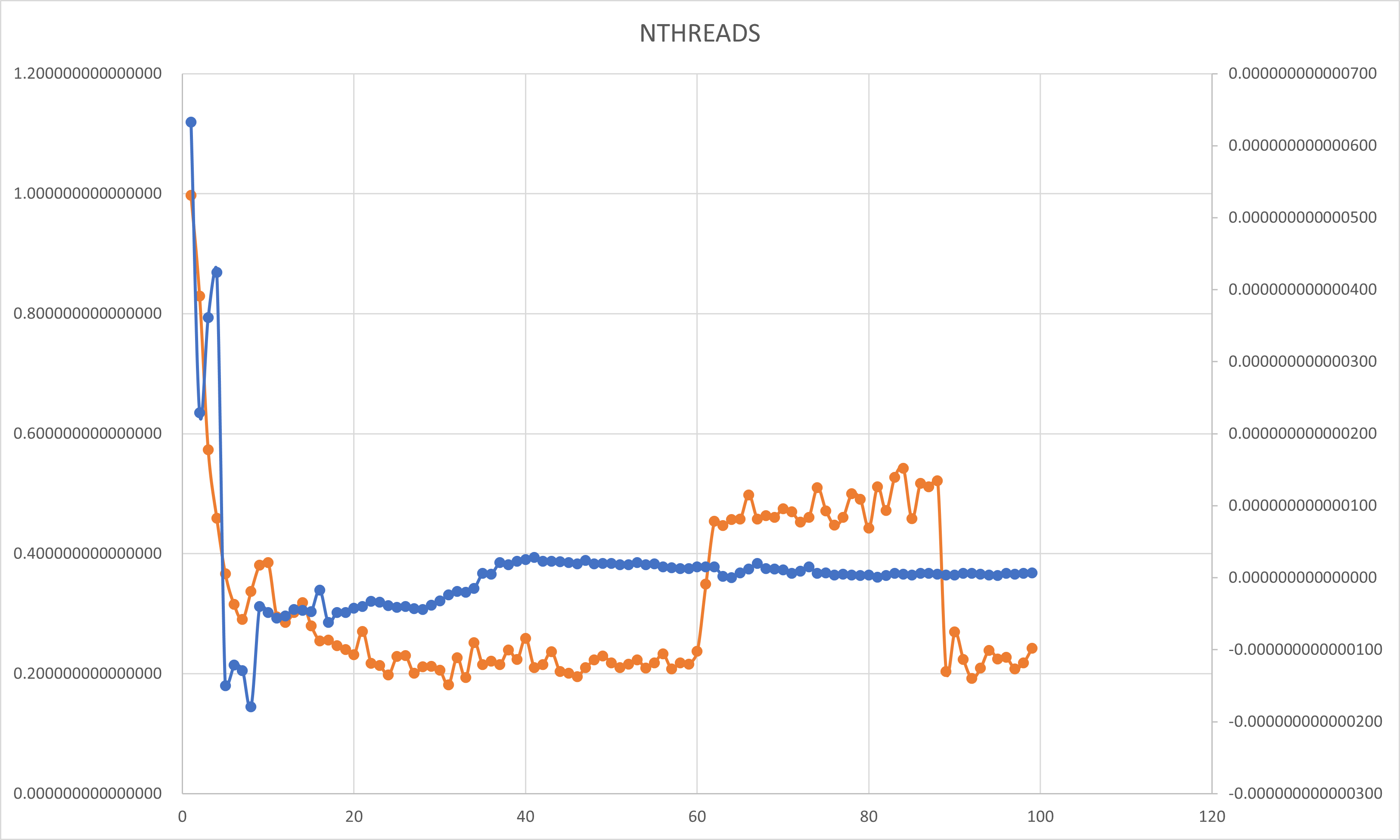
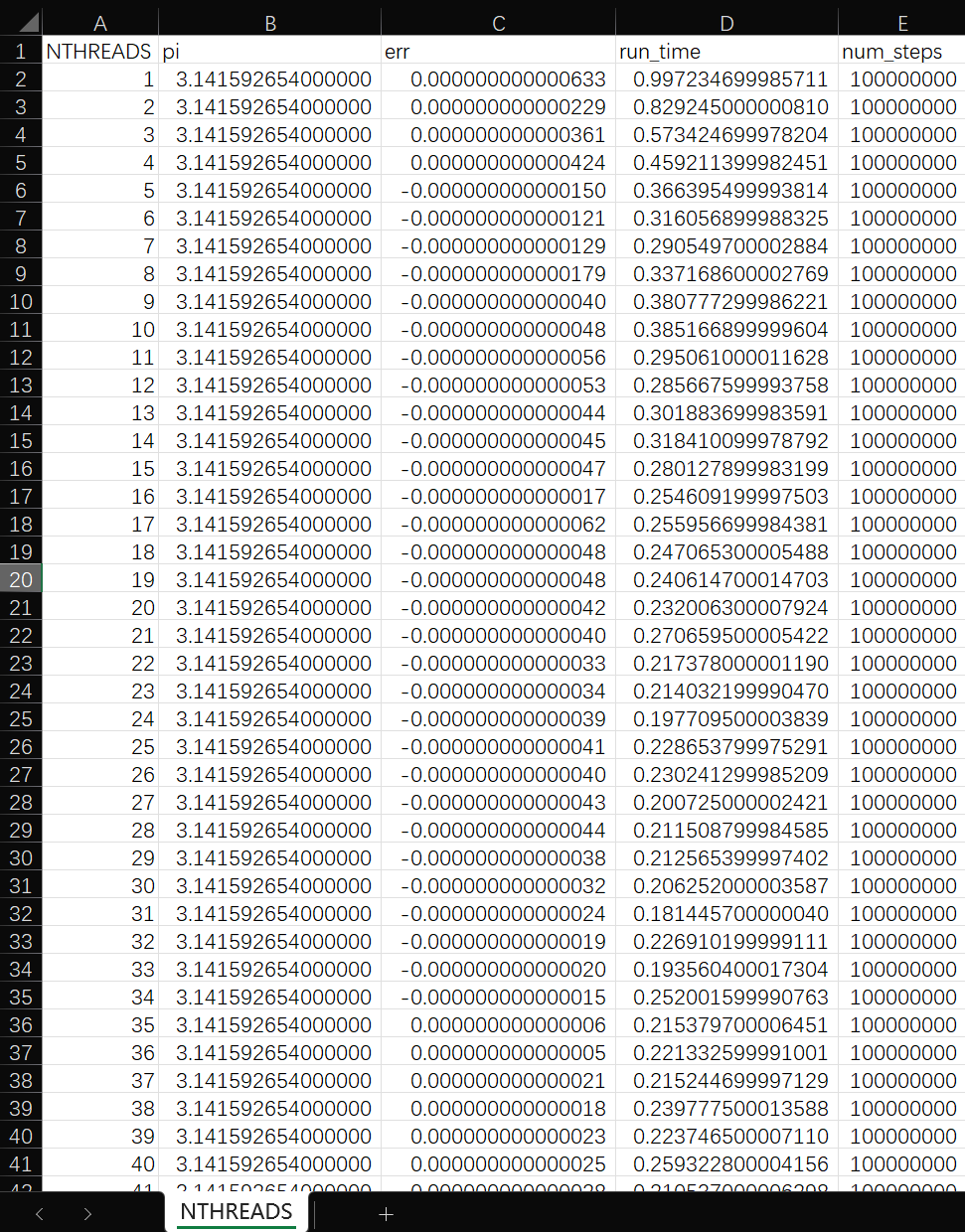
- 基于块分解划分循环迭代的SPMD并行数值积分:
- 不同步长情况
#include <iostream>
#include <omp.h>
#include <fstream>
#include <cmath>
import <format>;
#define TURNS 100
#define PI 3.141592653589793
long double num_steps = 1e9;
double step;
int main()
{
std::ofstream out;
out.open("example.csv", std::ios::ate);
out << "NTHREADS,pi,err,run_time,num_steps" << std::endl;
int NTHREADS = 10;
double sum[TURNS] = { 0,0 };
for (int j = 1; j < TURNS; j++) {
double start_time, run_time;
double pi, err;
pi = 0.0;
memset(sum, 0.0, sizeof(double) * NTHREADS);
int actual_nthreads;
step = 1.0 / (double)num_steps;
omp_set_num_threads(NTHREADS);
start_time = omp_get_wtime();
#pragma omp parallel
{
int id = omp_get_thread_num();
int numthreads = omp_get_num_threads();
double x;
if (id == 0)
actual_nthreads = numthreads;
int istart = id * num_steps / numthreads;
int iend = (id + 1) * num_steps / numthreads;
if (id == (numthreads - 1))
iend = num_steps;
for (int i = istart; i < iend; i++) {
x = (i + 0.5) * step;
sum[id] += 4.0 / (1.0 + x * x);
}
}//end of parallel
pi = 0.0;
for (int i = 0; i < actual_nthreads; i++)
pi += sum[i];
pi = step * pi;
err = pi - PI;
run_time = omp_get_wtime() - start_time;
std::cout << std::format("pi is {} in {} seconds {} thrds.step is {},err is {}",
pi,
run_time,
actual_nthreads,
step,
err
) << std::endl;
out << std::format("{},{:.15f},{:.15f},{:.15f},{}",
NTHREADS,
pi,
err,
run_time,
num_steps
) << std::endl;
num_steps /= 2.0;
}
out.close();
return 0;
}
- 不同线程数情况
#include <iostream>
#include <omp.h>
#include <fstream>
import <format>;
#define TURNS 100
#define PI 3.141592653589793
long double num_steps = 1e8;
double step;
int main()
{
std::ofstream out;
out.open("example.csv", std::ios::ate);
out << "NTHREADS,pi,err,run_time,num_steps" << std::endl;
double sum[TURNS] = { 0,0 };
for (int NTHREADS = 1; NTHREADS < TURNS; NTHREADS++) {
double start_time, run_time;
double pi, err;
pi = 0.0;
memset(sum, 0.0, sizeof(double) * NTHREADS);
int actual_nthreads;
step = 1.0 / (double)num_steps;
omp_set_num_threads(NTHREADS);
start_time = omp_get_wtime();
#pragma omp parallel
{
int id = omp_get_thread_num();
int numthreads = omp_get_num_threads();
double x;
if (id == 0)
actual_nthreads = numthreads;
int istart = id * num_steps / numthreads;
int iend = (id + 1) * num_steps / numthreads;
if (id == (numthreads - 1))
iend = num_steps;
for (int i = istart; i < iend; i++) {
x = (i + 0.5) * step;
sum[id] += 4.0 / (1.0 + x * x);
}
}//end of parallel
pi = 0.0;
for (int i = 0; i < actual_nthreads; i++)
pi += sum[i];
pi = step * pi;
err = pi - PI;
run_time = omp_get_wtime() - start_time;
std::cout << std::format("pi is {} in {} seconds {} thrds.step is {},err is {}",
pi,
run_time,
actual_nthreads,
step,
err
) << std::endl;
out << std::format("{},{:.15f},{:.15f},{:.15f},{}",
NTHREADS,
pi,
err,
run_time,
num_steps
) << std::endl;
}
out.close();
return 0;
}
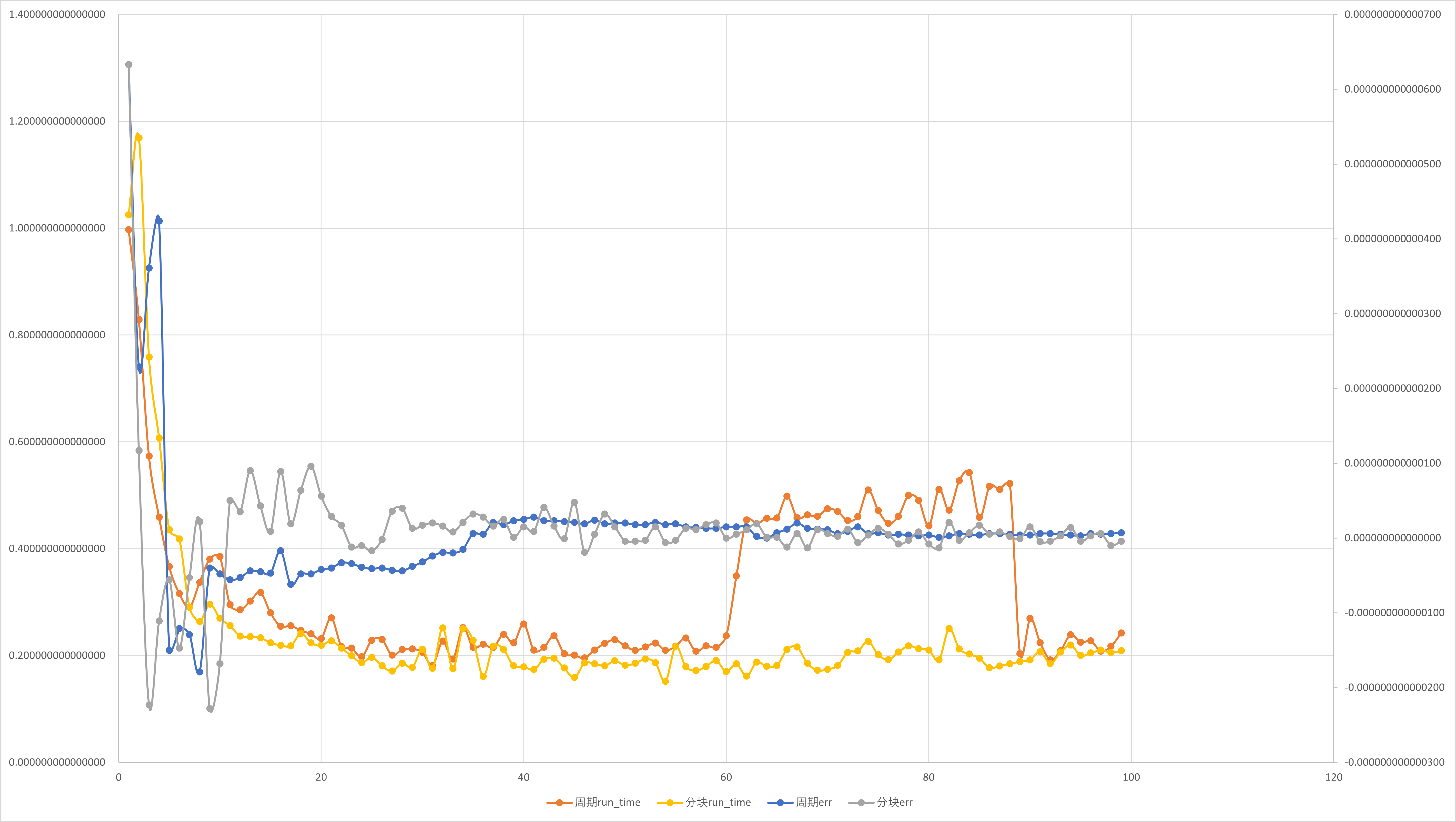
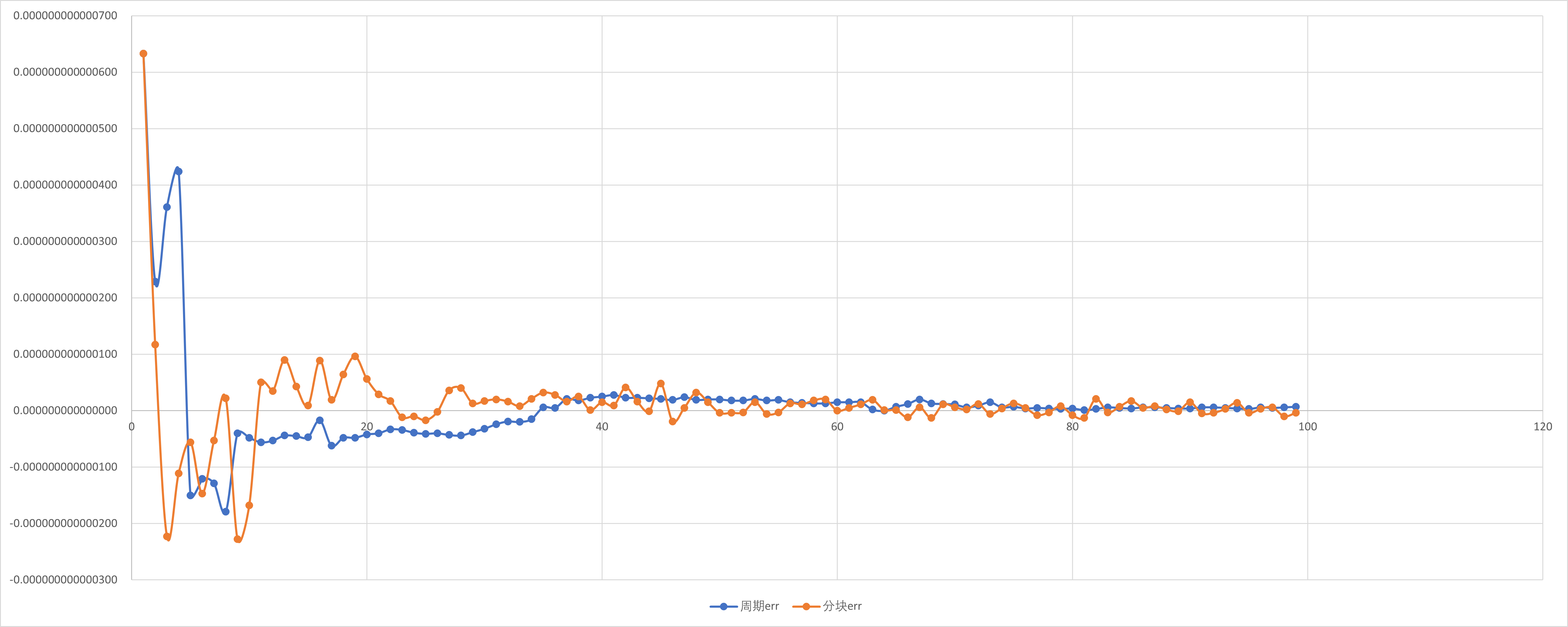
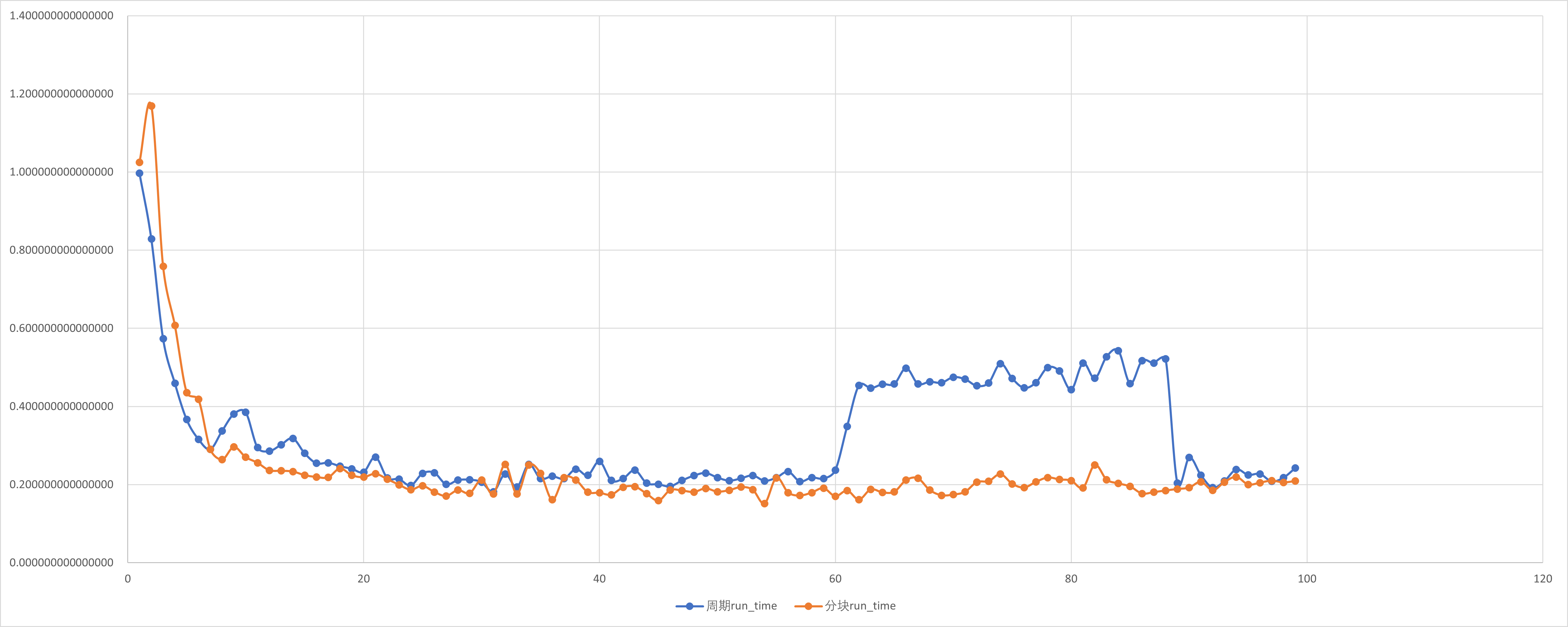
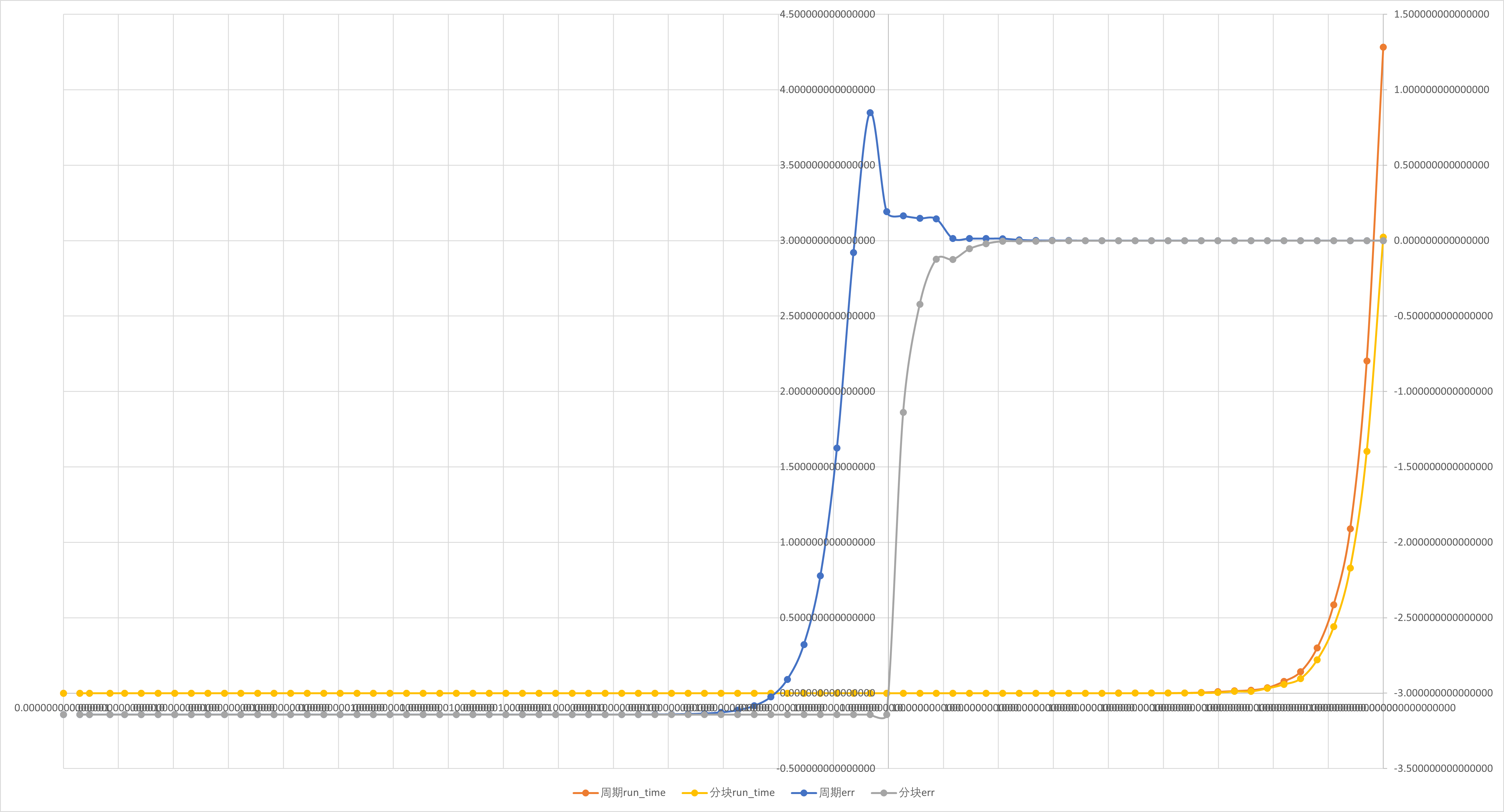
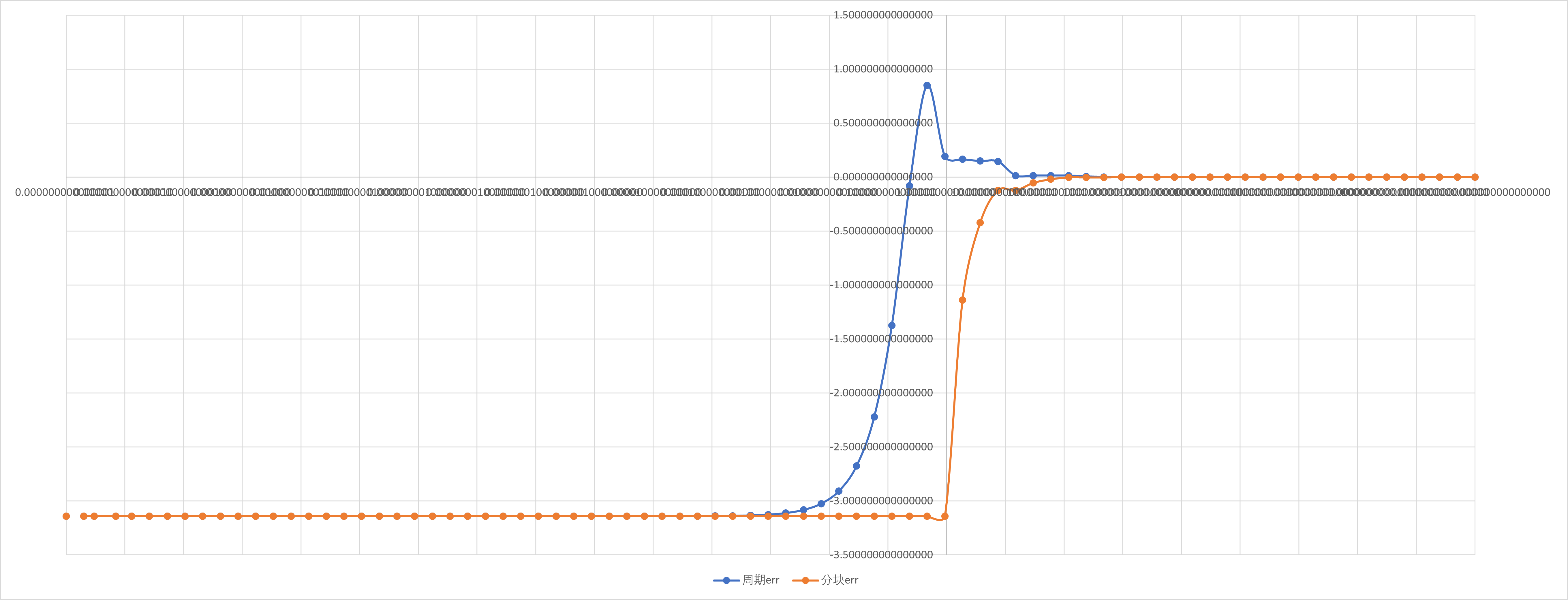
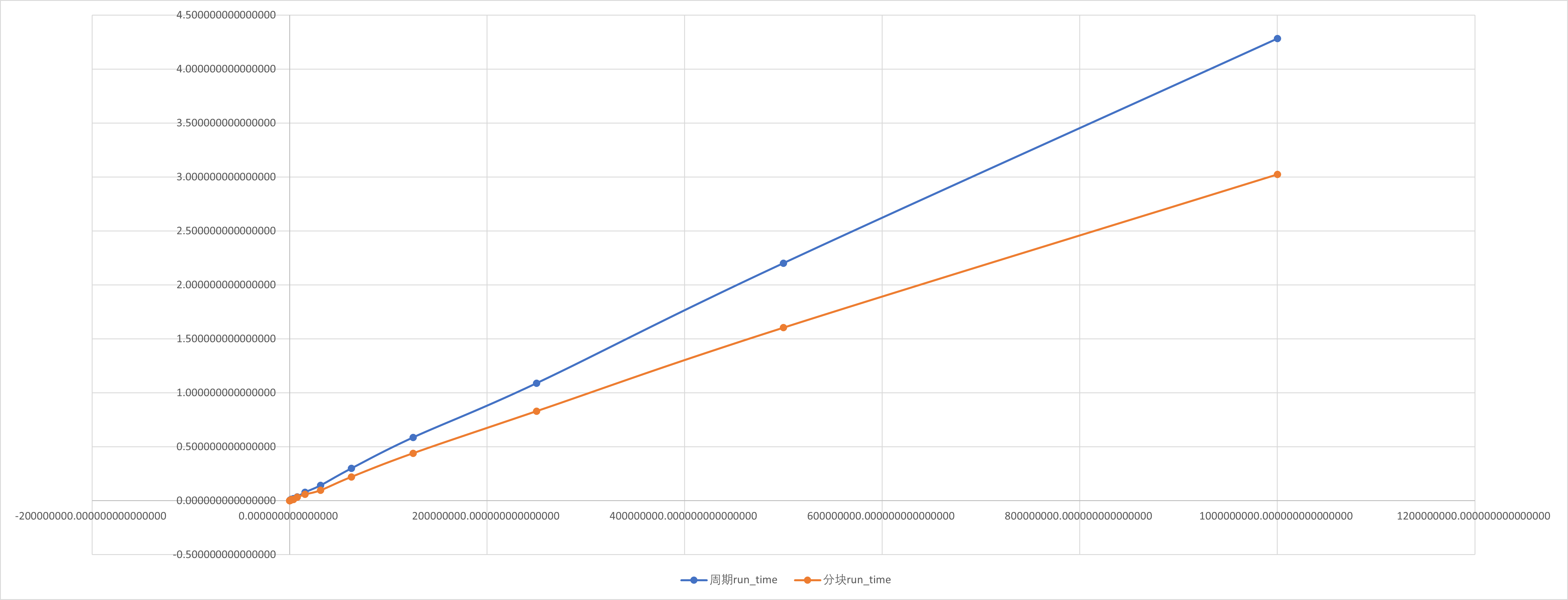
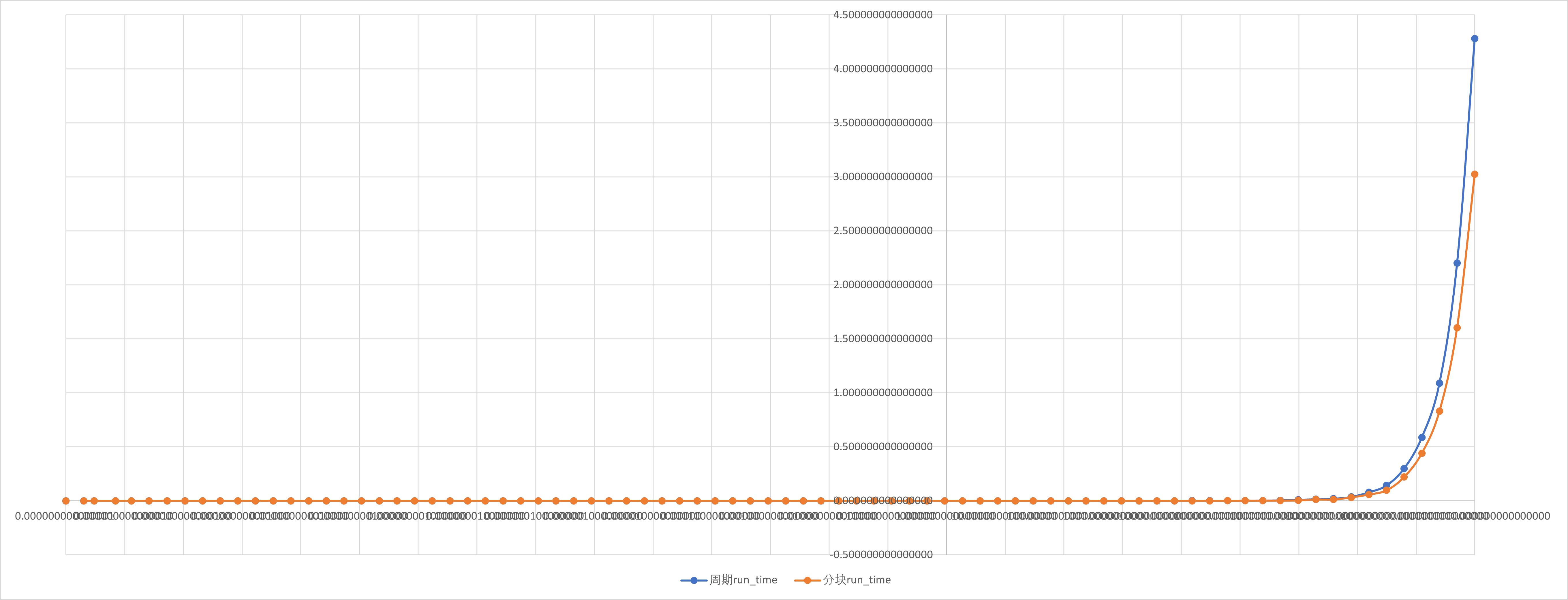
加速比与并行效率分析
在前面的学习过程中,我们已经了解到了加速比与并行效率的定义:
加速比S(P): 加速比是一个程序运行时间的比率.理想情况下,在一个处理器上用可获得的最好串行算法运行一个程序,然后用并行软件在P个处理器上再次运行它.
如果定义$T_S$为串行程序的运行时间,定义$T_P$为在P个处理器上的并行程序的运行时间,那么加速比的定义为:
$$S(P)=\dfrac{T_S}{T_P}$$
在理想的情况下,加速比等于处理器的数量.
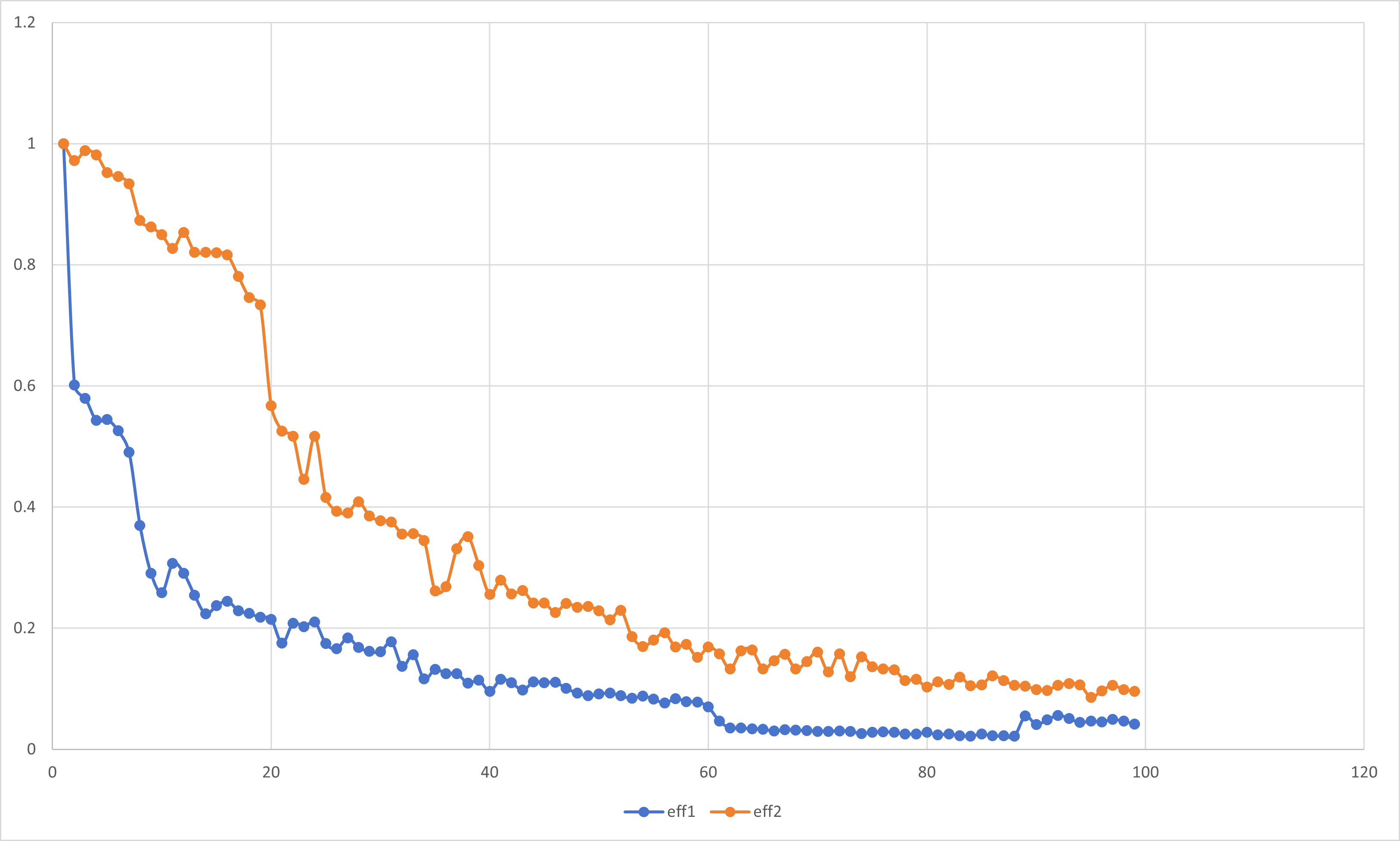
并行效率eff: 用于衡量可缩放的加速比与完美线性加速比接近程度的量.
$$eff=\dfrac{S(P)}{P}$$
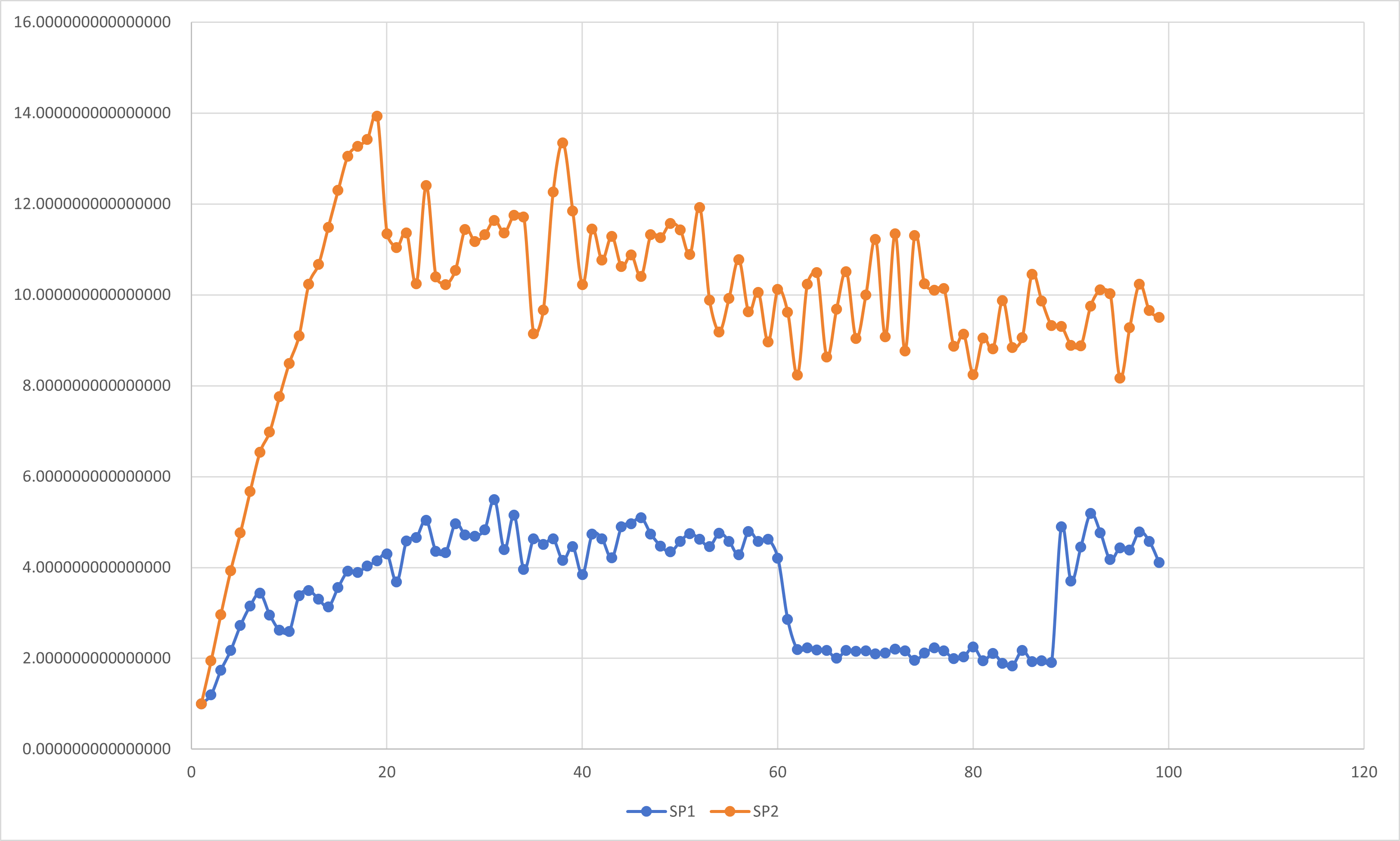
按照定义,我们对前文所述实验内容进行分析.
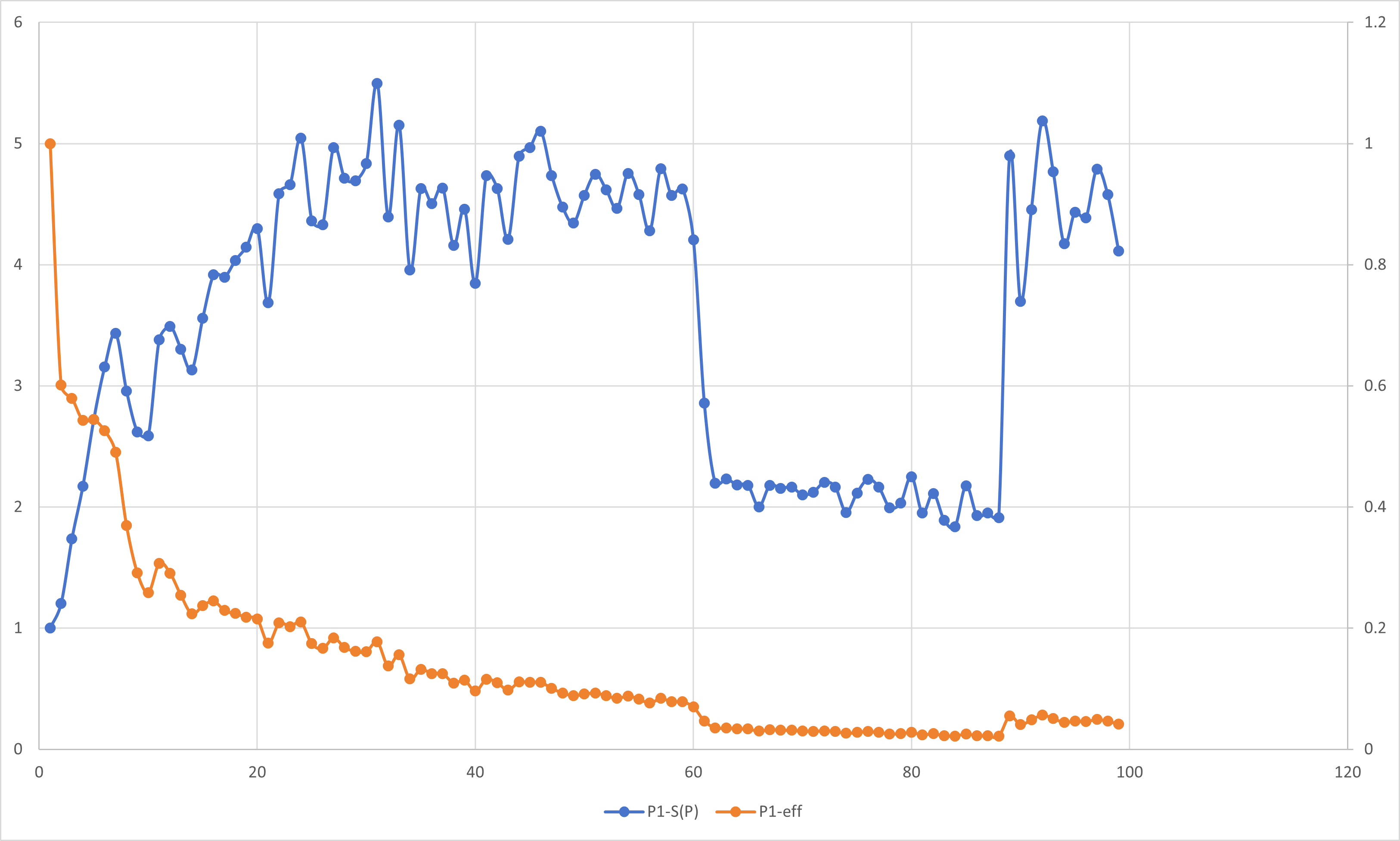
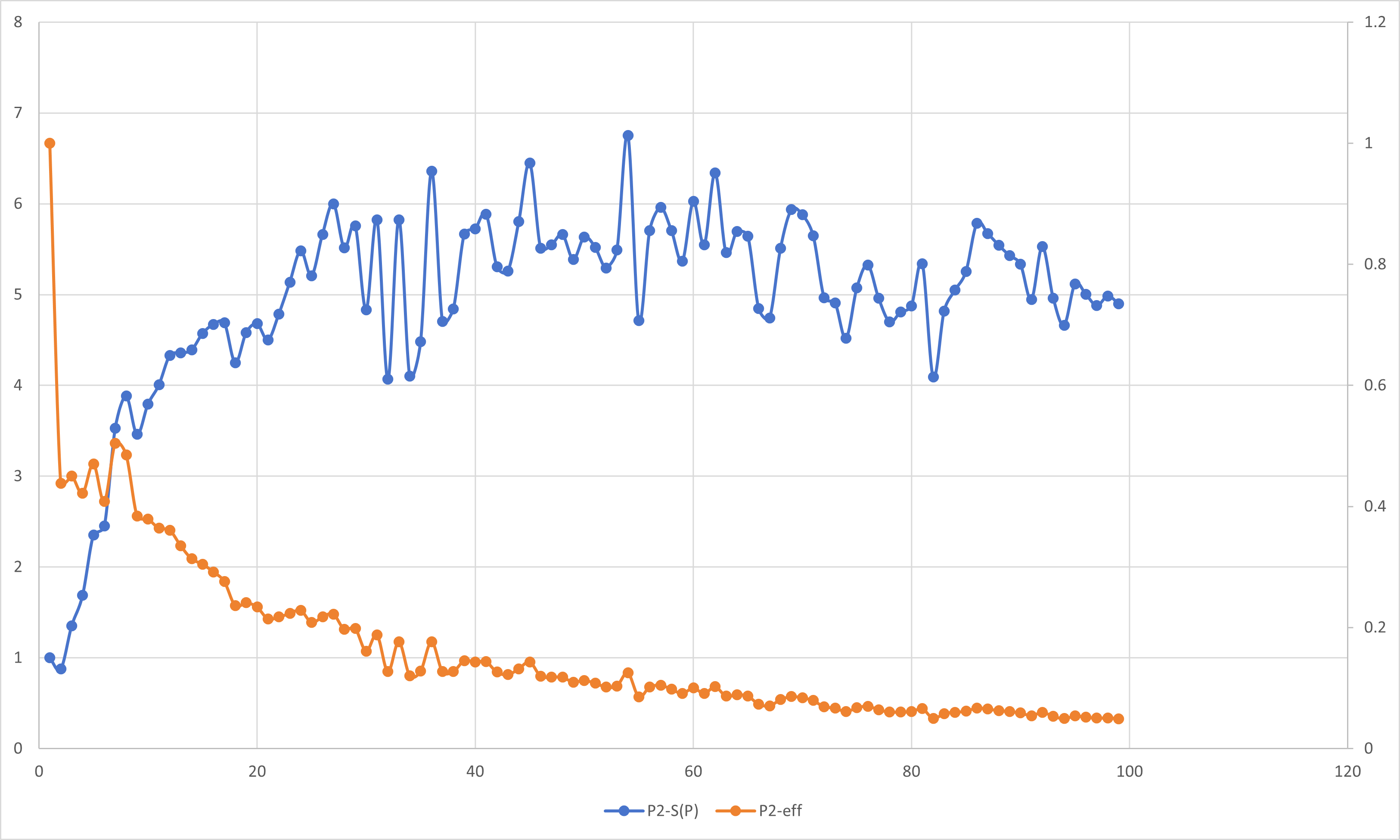
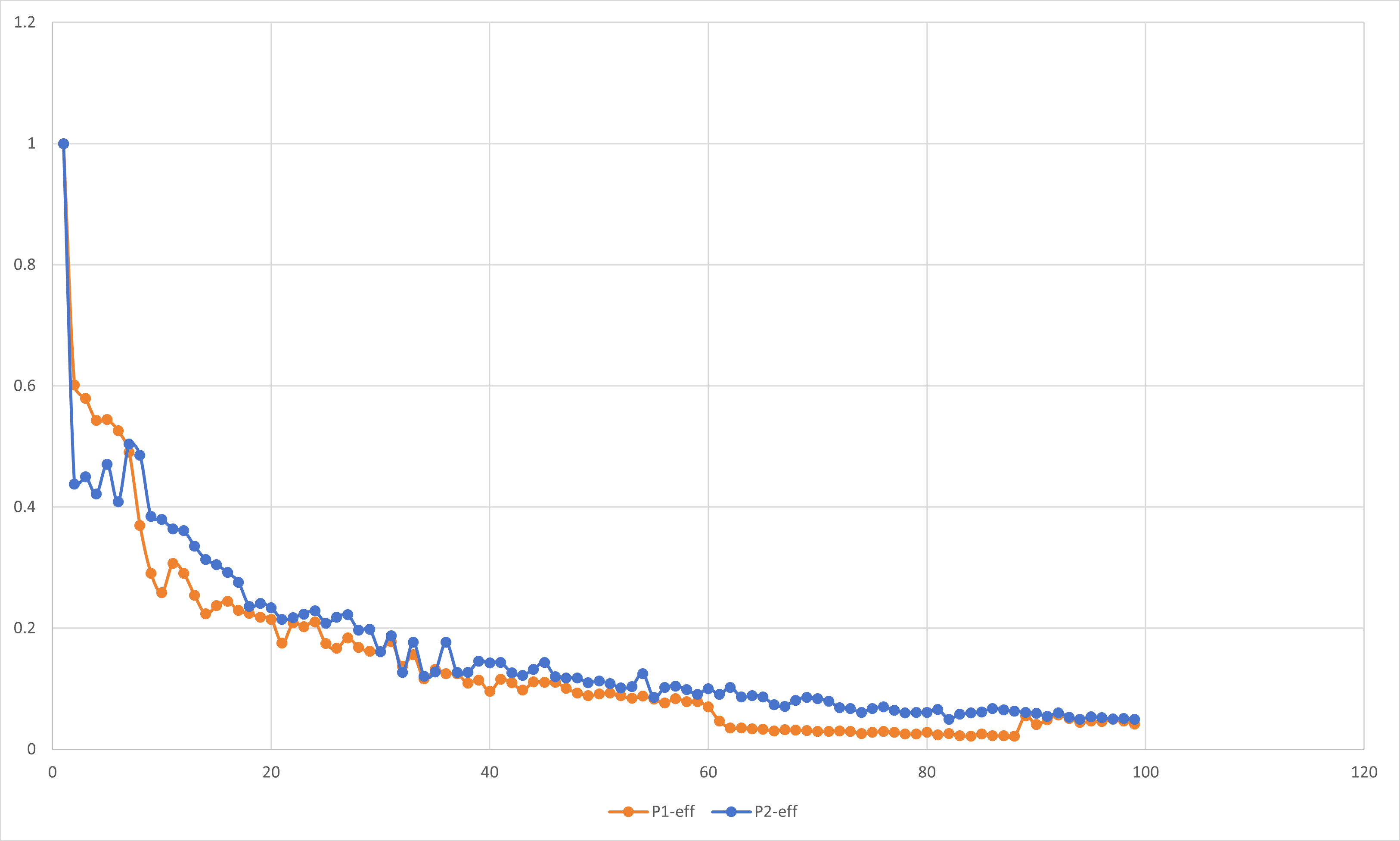
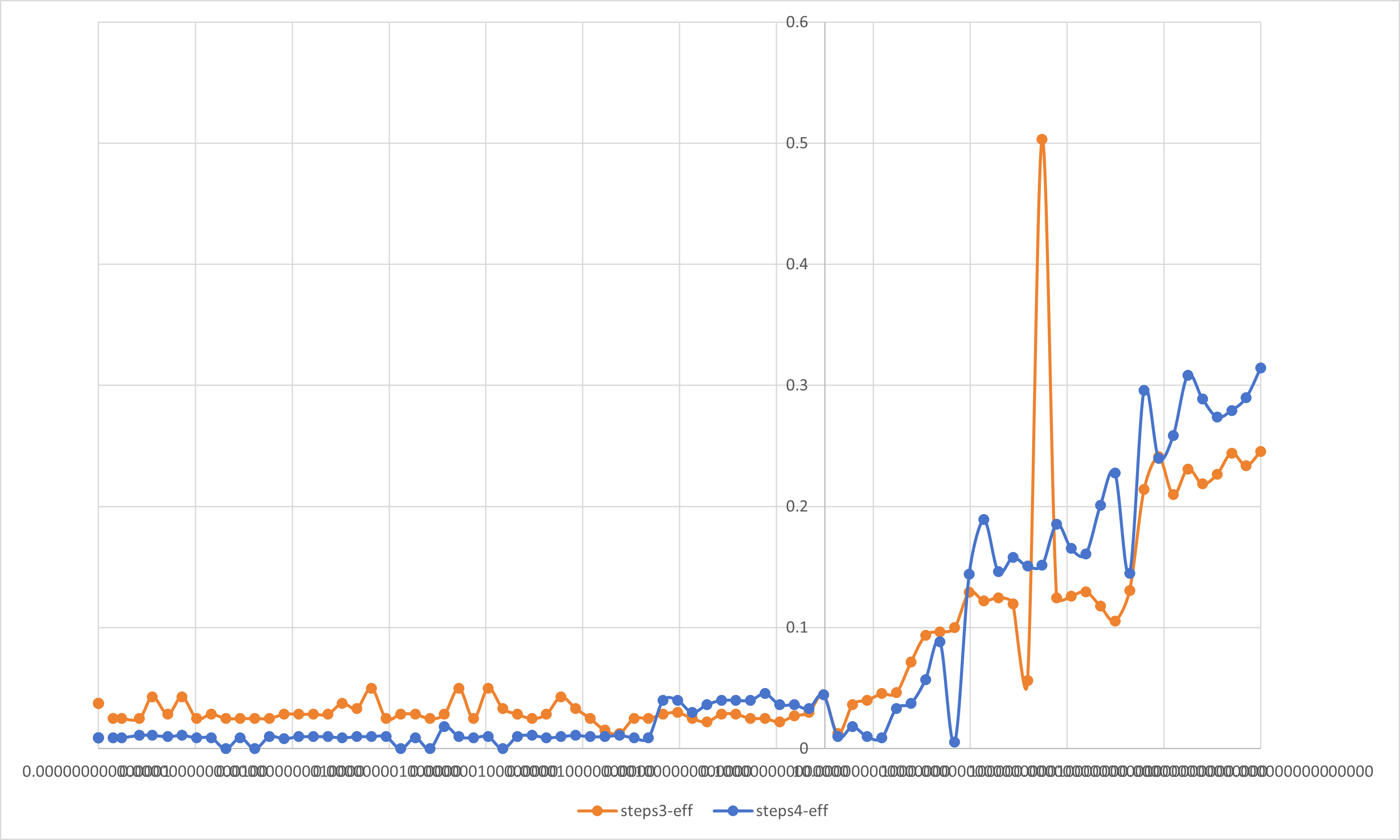
周期分布与块状分解只是在一组线程中划分循环迭代的两种方法.还有很多方法可以完成这一任务.
伪共享
空间的局限性: 如果一个线程访问数组的某个元素,那么随后对该数组的内存引用最有可能是紧接着的元素.
伪共享: 为了利用空间局限性,相邻数组元素倾向于在同一个共享的L1 缓冲行中.当独立的数据元素恰好是同一个高速缓存行的一部分时,每次更新都会导致高速缓存行在核心之间 来回移动.这种多余的内存流动会极大地降低程序的速度.
为了消除伪共享,一种方法是填充出现伪共享的数组,使其大到足以填满L1缓存行.(8个4字节数=32字节)
下面我们在基于按周期分布划分循环迭代的不同线程数的SPMD并行数值积分基础上消除伪并行进行比较:
#include <iostream>
#include <omp.h>
#include <fstream>
import <format>;
#define TURNS 100
#define PI 3.141592653589793
#define CBLK 8
long double num_steps = 1e8;
double step;
int main()
{
std::ofstream out;
out.open("example.csv", std::ios::ate);
out << "NTHREADS,pi,err,run_time,num_steps" << std::endl;
double sum[TURNS][CBLK] = { 0,0 };
for (int NTHREADS = 1; NTHREADS < TURNS; NTHREADS++) {
double start_time, run_time;
double pi, err;
pi = 0.0;
memset(sum, 0.0, sizeof(double) * NTHREADS * CBLK);
int actual_nthreads;
step = 1.0 / (double)num_steps;
omp_set_num_threads(NTHREADS);
start_time = omp_get_wtime();
#pragma omp parallel
{
int id = omp_get_thread_num();
int numthreads = omp_get_num_threads();
double x;
if (id == 0)
actual_nthreads = numthreads;
for (int i = id; i < num_steps; i += numthreads) {
x = (i + 0.5) * step;
sum[id][0] += 4.0 / (1.0 + x * x);
}
}//end of parallel
pi = 0.0;
for (int i = 0; i < actual_nthreads; i++)
pi += sum[i][0];
pi = step * pi;
err = pi - PI;
run_time = omp_get_wtime() - start_time;
std::cout << std::format("pi is {} in {} seconds {} thrds.step is {},err is {}",
pi,
run_time,
actual_nthreads,
step,
err
)<<std::endl;
out << std::format("{},{:.15f},{:.15f},{:.15f},{}",
NTHREADS,
pi,
err,
run_time,
num_steps
) << std::endl;
}
out.close();
return 0;
}
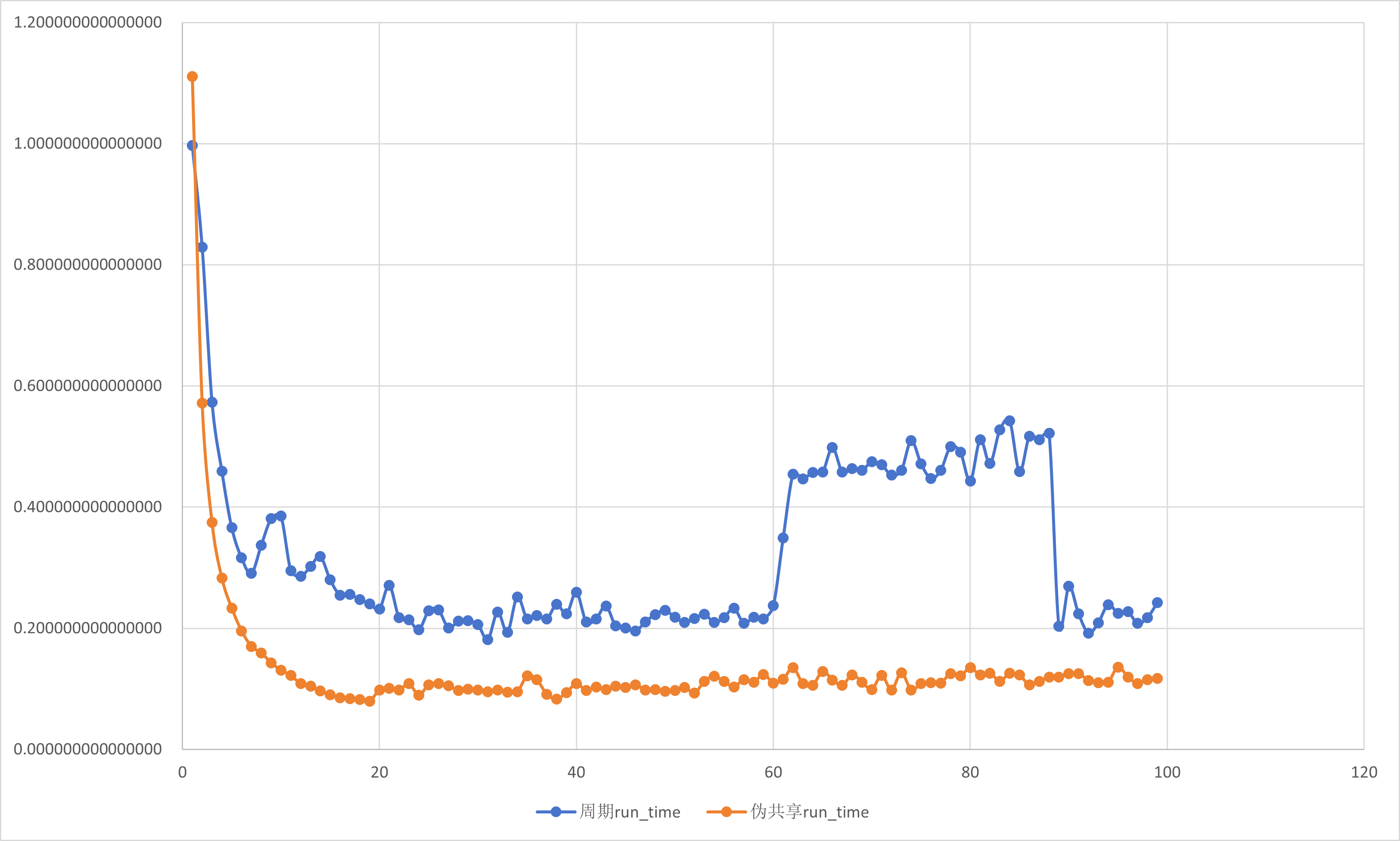
使用数组作为累加器会导致伪共享问题.如果可以在一个线程执行的结构化块的作用域内使用标量,那么变量很可能不会存储在同一缓存行中,伪共享就是不可能的.谓词,需要重新审视共享变量.
同步
在OpenMP通用核心中,有两种同步机制: 临界区 和 栅栏.
临界区: 为多线程运行的代码提供了一种相互排斥关系.如果一个线程与另一个线程同时试图执行同样的代码块,那么第二个线程将暂停并等待,直到第一个线程执行完成.
- 通过critical构造实现临界区:
#pragma omp critical
{
//etc codes...
}
在大多数情况下,使用临界区的最大开销来自等待执行代码的线程.
下面我们在基于按周期分布划分循环迭代的不同线程数的SPMD并行数值积分基础上使用临界区消除对累加器的需求进行比较:
#include <iostream>
#include <omp.h>
#include <fstream>
import <format>;
#define TURNS 100
#define PI 3.141592653589793
long double num_steps = 1e8;
double step;
int main()
{
std::ofstream out;
out.open("example.csv", std::ios::ate);
out << "NTHREADS,pi,err,run_time,num_steps" << std::endl;
double sum = 0.0;
for (int NTHREADS = 1; NTHREADS < TURNS; NTHREADS++) {
double start_time, run_time;
double pi, err;
pi = sum = 0.0;
int actual_nthreads;
step = 1.0 / (double)num_steps;
omp_set_num_threads(NTHREADS);
start_time = omp_get_wtime();
#pragma omp parallel
{
int id = omp_get_thread_num();
int numthreads = omp_get_num_threads();
double x;
double partial = 0.0;
if (id == 0)
actual_nthreads = numthreads;
int istart = id * num_steps / numthreads;
int iend = (id + 1) * num_steps / numthreads;
if (id == (numthreads - 1))
iend = num_steps;
for (int i = istart; i < iend; i++) {
x = (i + 0.5) * step;
partial += 4.0 / (1.0 + x * x);
}
#pragma omp critical
sum += partial;
}//end of parallel
pi = step * sum;
err = pi - PI;
run_time = omp_get_wtime() - start_time;
std::cout << std::format("pi is {} in {} seconds {} thrds.step is {},err is {}",
pi,
run_time,
actual_nthreads,
step,
err
) << std::endl;
out << std::format("{},{:.15f},{:.15f},{:.15f},{}",
NTHREADS,
pi,
err,
run_time,
num_steps
) << std::endl;
}
out.close();
return 0;
}
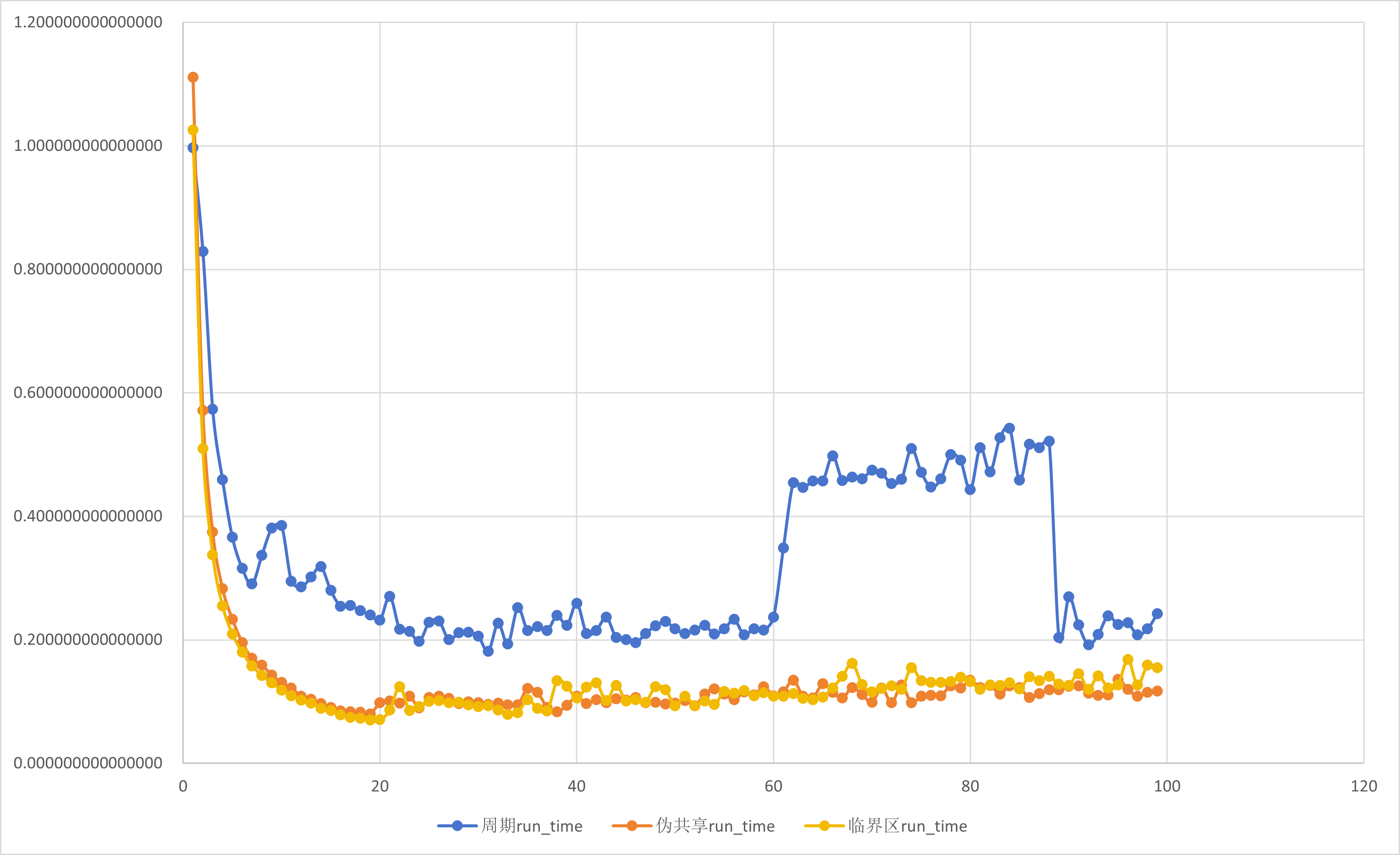
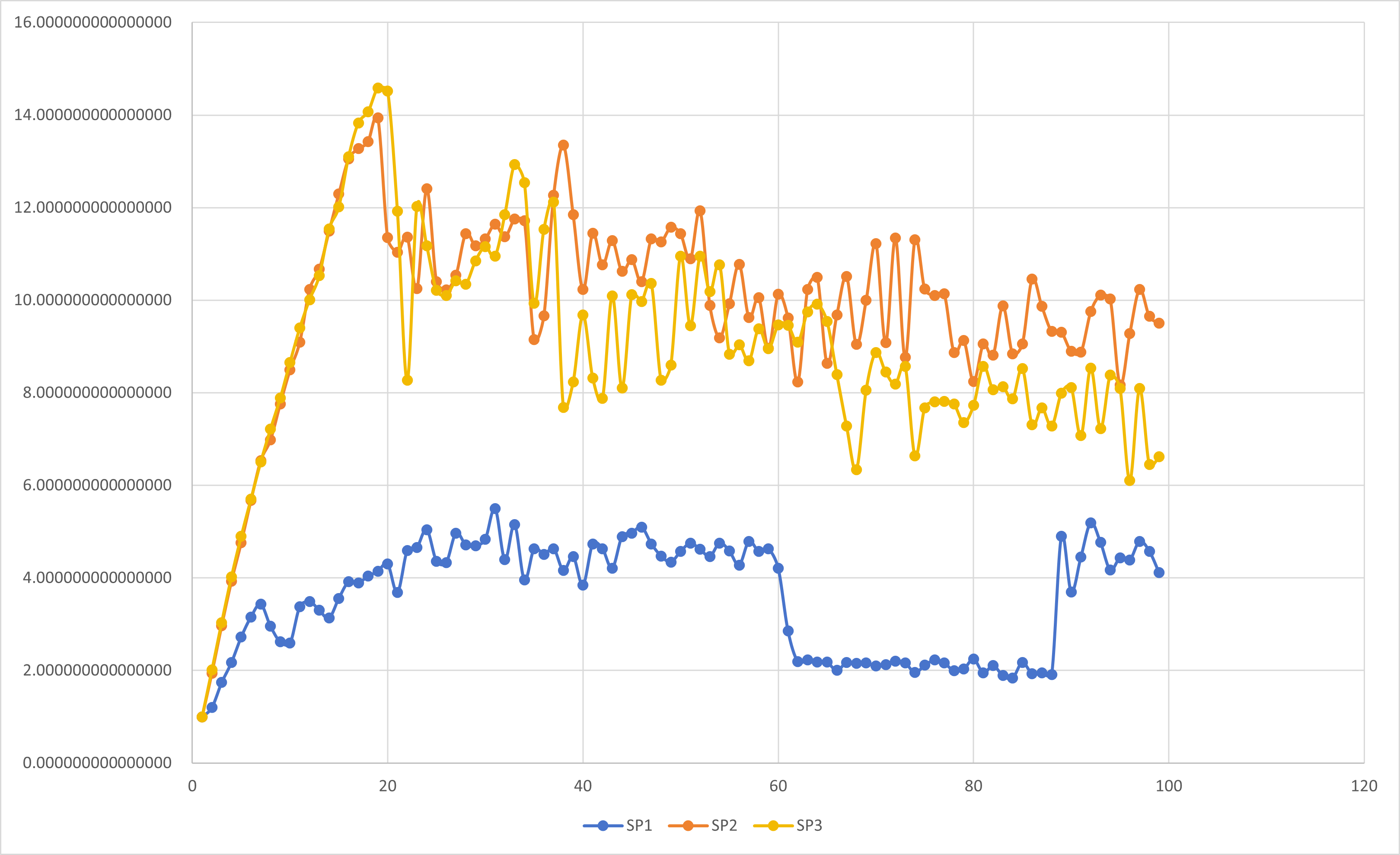
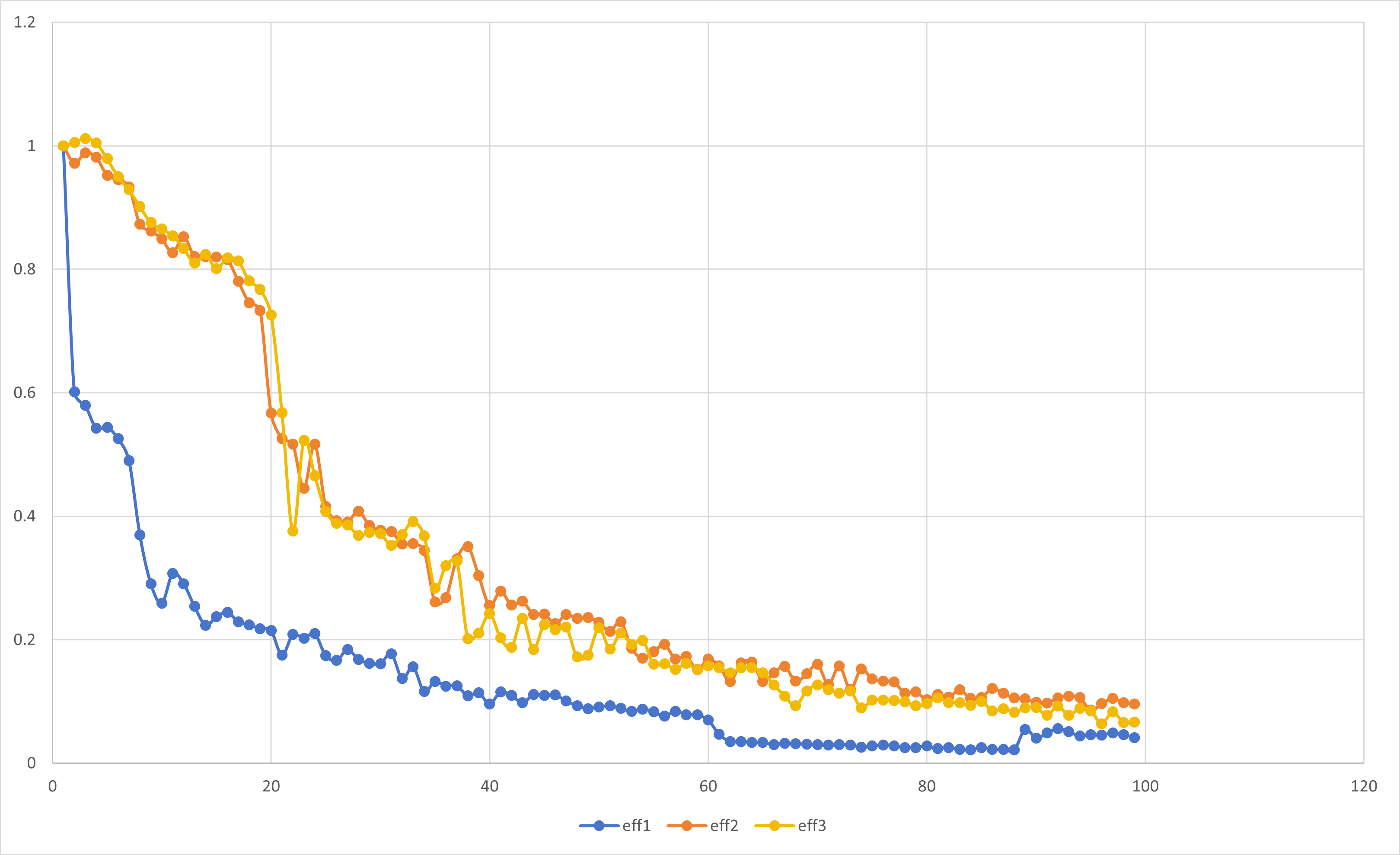
注意到, 使用临界区的代码性能与填充数组消除伪共享的结果的性能非常匹配,证实了主要问题是伪共享.
栅栏(barrier): 栅栏定义了程序中的一个点,在这个点上,所有线程必须在任意线程通过栅栏之前到达.每一个并行区域的结束都隐含着一个栅栏.
- 插入一个显示栅栏的指令:
#pragma omp barrier
栅栏可能是成本很高的.任何时候线程都在同步构造处等待,;有用的工作不会由这些线程完成,这直接转化为并行开销.
