哈尔滨工程大学 ACM程序设计 2023年下期 作业题及题解整理
A+B Problem(高精)
题目描述
高精度加法,相当于 a+b problem,不用考虑负数。
输入格式
分两行输入。$a,b \leq 10^{500}$。
输出格式
输出只有一行,代表 $a+b$ 的值。
样例 #1
样例输入 #1
1
1
样例输出 #1
2
样例 #2
样例输入 #2
1001
9099
样例输出 #2
10100
提示
$20%$ 的测试数据,$0\le a,b \le10^9$;
$40%$ 的测试数据,$0\le a,b \le10^{18}$。
#include <iostream>
using namespace std;
string add(string a, string b){
int a_len=a.length();
int b_len=b.length();
//进行补0操作
if(a_len>b_len){
for(int i=0; i < a_len-b_len; i ++){
b='0'+b;
}
}else{
for(int i=0; i < b_len-a_len; i ++){
a='0'+a;
}
}
int carry = 0;
string result;
int temp;
int length = a.length();
for(int i = length-1; i>=0; i--){
temp = a[i]-'0'+b[i]-'0'+carry;
result= char(temp%10+'0') + result;
carry = temp/10;
}
if(carry !=0){
result = char(carry+'0') + result;
}
return result;
}
int main(){
string a, b;
cin >> a >> b;
cout << add(a, b);
}
A*B Problem
题目描述
给出两个非负整数,求它们的乘积。
输入格式
输入共两行,每行一个非负整数。
输出格式
输出一个非负整数表示乘积。
样例 #1
样例输入 #1
1
2
样例输出 #1
2
提示
每个非负整数不超过 $10^{2000}$。
#include <iostream>
using namespace std;
void getResult(string a, string b){
int a_len = a.length();
int b_len = b.length();
int ag[a_len+5];
int bg[b_len+5];
//得到a, b的数组
for(int i = 0; i < a_len; i ++){
ag[i] = a[a_len-i-1] - '0';
}
for(int i = 0; i < b_len; i ++)
bg[i] = b[b_len-i-1] - '0';
//c的数组定义与初始化
int c_len = a_len + b_len;
int c[c_len+5];
for(int i = 0; i < c_len; i ++){
c[i] = 0;
}
//处理c数组
for(int i = 0; i < b_len; i ++){
for(int j = 0; j < a_len; j ++){
c[i+j]+=bg[j]*ag[i];
}
}
for(int i = 0; i < c_len; i++){
c[i+1]+=c[i]/10;
c[i]=c[i] % 10;
}
//输出结果
int flag = 0;
for(int i=c_len-1; i>=0; i --){
if(c[i] != 0){
flag = 1;
}
if(flag == 1){
cout << c[i];
}
}
if(flag == 0){
cout << 0;
}
}
int main(){
string a, b;
cin >> a >> b;
getResult(a, b);
}
【模板】排序
题目描述
将读入的 $N$ 个数从小到大排序后输出。
输入格式
第一行为一个正整数 $N$。
第二行包含 $N$ 个空格隔开的正整数 $a_i$,为你需要进行排序的数。
输出格式
将给定的 $N$ 个数从小到大输出,数之间空格隔开,行末换行且无空格。
样例 #1
样例输入 #1
5
4 2 4 5 1
样例输出 #1
1 2 4 4 5
提示
对于 $20%$ 的数据,有 $1 \leq N \leq 10^3$;
对于 $100%$ 的数据,有 $1 \leq N \leq 10^5$,$1 \le a_i \le 10^9$。
#include <iostream>
//sort排序的头文件
#include <algorithm>
using namespace std;
int main() {
int n;
//键入个数
cin >> n;
int arr[n];
//键入元素
for (int i = 0; i < n; ++i) {
cin >> arr[i];
}
//sort排序,底层是快速排序
//第一个参数代表开始地址,第二个参数代表结束地址,可以传入第三个参数:排序规则(默认升序排)
sort(arr, arr + n);
//打印结果
for (int i = 0; i < n; ++i) {
cout << arr[i] << " ";
}
return 0;
}
生日
题目描述
cjf 君想调查学校 OI 组每个同学的生日,并按照年龄从大到小的顺序排序。但 cjf 君最近作业很多,没有时间,所以请你帮她排序。
输入格式
输入共有 $n + 1$ 行,
第 $1$ 行为 OI 组总人数 $n$;
第 $2$ 行至第 $n+1$ 行分别是每人的姓名 $s$、出生年 $y$、月 $m$、日 $d$。
输出格式
输出共有 $n$ 行,
即 $n$ 个生日从大到小同学的姓名。(如果有两个同学生日相同,输入靠后的同学先输出)
样例 #1
样例输入 #1
3
Yangchu 1992 4 23
Qiujingya 1993 10 13
Luowen 1991 8 1
样例输出 #1
Luowen
Yangchu
Qiujingya
提示
数据保证,$1<n<100$,$1\leq |s|<20$。保证年月日实际存在,且年份 $\in [1960,2020]$。
#include <iostream>
using namespace std;
class Student{
public:
string name;
int year;
int month;
int day;
int statis;
};
int main(){
int n;
cin >> n;
Student stu[n+5];
for(int i = 0; i < n; i ++){
cin >> stu[i].name >> stu[i].year >> stu[i].month >> stu[i].day;
stu[i].statis = stu[i].year*10000 + stu[i].month*100 + stu[i].day;
}
Student p;
//从小排到大,直接插入排序
for(int i = 1; i < n; i ++){
if(stu[i].statis <= stu[i - 1].statis){
p = stu[i];
int j = 0;
for(j = i - 1; stu[j].statis >= p.statis; j --){
stu[j+1] = stu[j];
}
stu[j+1] = p;
}
}
for(int i = 0; i < n; i ++){
cout << stu[i].name << endl;
}
}
[NOIP2009 普及组] 分数线划定
题目描述
世博会志愿者的选拔工作正在 A 市如火如荼的进行。为了选拔最合适的人才,A 市对所有报名的选手进行了笔试,笔试分数达到面试分数线的选手方可进入面试。面试分数线根据计划录取人数的 $150%$ 划定,即如果计划录取 $m$ 名志愿者,则面试分数线为排名第 $m \times 150%$(向下取整)名的选手的分数,而最终进入面试的选手为笔试成绩不低于面试分数线的所有选手。
现在就请你编写程序划定面试分数线,并输出所有进入面试的选手的报名号和笔试成绩。
输入格式
第一行,两个整数 $n,m(5 \leq n \leq 5000,3 \leq m \leq n)$,中间用一个空格隔开,其中 $n$ 表示报名参加笔试的选手总数,$m$ 表示计划录取的志愿者人数。输入数据保证 $m \times 150%$ 向下取整后小于等于 $n$。
第二行到第 $n+1$ 行,每行包括两个整数,中间用一个空格隔开,分别是选手的报名号 $k(1000 \leq k \leq 9999)$和该选手的笔试成绩 $s(1 \leq s \leq 100)$。数据保证选手的报名号各不相同。
输出格式
第一行,有 $2$ 个整数,用一个空格隔开,第一个整数表示面试分数线;第二个整数为进入面试的选手的实际人数。
从第二行开始,每行包含 $2$ 个整数,中间用一个空格隔开,分别表示进入面试的选手的报名号和笔试成绩,按照笔试成绩从高到低输出,如果成绩相同,则按报名号由小到大的顺序输出。
样例 #1
样例输入 #1
6 3
1000 90
3239 88
2390 95
7231 84
1005 95
1001 88
样例输出 #1
88 5
1005 95
2390 95
1000 90
1001 88
3239 88
提示
【样例说明】
$m \times 150% = 3 \times150% = 4.5$,向下取整后为 $4$。保证 $4$ 个人进入面试的分数线为 $88$,但因为 $88$ 有重分,所以所有成绩大于等于 $88$ 的选手都可以进入面试,故最终有 $5$ 个人进入面试。
NOIP 2009 普及组 第二题
#include<bits/stdc++.h>
using namespace std;
struct r {
int NO;
int f;
};
r arr[10000];
bool cmp(r a, r b) {
if (a.f > b.f) return 1;
if (a.f < b.f) return 0;
if (a.NO < b.NO) return 1;
if (a.NO > b.NO) return 0;
}
int main() {
int n, m;
cin >> n >> m;
m *= 1.5;
for (int i = 1; i <= n; i++) cin >> arr[i].NO >> arr[i].f;
sort(arr + 1, arr + n + 1, cmp);
cout << arr[m].f << ' ';
for (int i = m + 1; i <= n; i++) {
if (arr[i].f == arr[m].f) {
m++;
} else {
break;
}
}
cout << m << endl;
for (int i = 1; i <= m; i++) {
cout << arr[i].NO << ' ' << arr[i].f << endl;
}
return 0;
}
[NOIP2012 提高组] 国王游戏
题目描述
恰逢 H 国国庆,国王邀请 $n$ 位大臣来玩一个有奖游戏。首先,他让每个大臣在左、右手上面分别写下一个整数,国王自己也在左、右手上各写一个整数。然后,让这 $n$ 位大臣排成一排,国王站在队伍的最前面。排好队后,所有的大臣都会获得国王奖赏的若干金币,每位大臣获得的金币数分别是:排在该大臣前面的所有人的左手上的数的乘积除以他自己右手上的数,然后向下取整得到的结果。
国王不希望某一个大臣获得特别多的奖赏,所以他想请你帮他重新安排一下队伍的顺序,使得获得奖赏最多的大臣,所获奖赏尽可能的少。注意,国王的位置始终在队伍的最前面。
输入格式
第一行包含一个整数 $n$,表示大臣的人数。
第二行包含两个整数 $a$ 和 $b$,之间用一个空格隔开,分别表示国王左手和右手上的整数。
接下来 $n$ 行,每行包含两个整数 $a$ 和 $b$,之间用一个空格隔开,分别表示每个大臣左手和右手上的整数。
输出格式
一个整数,表示重新排列后的队伍中获奖赏最多的大臣所获得的金币数。
样例 #1
样例输入 #1
3
1 1
2 3
7 4
4 6
样例输出 #1
2
提示
【输入输出样例说明】
按 $1$、$2$、$3$ 这样排列队伍,获得奖赏最多的大臣所获得金币数为 $2$;
按 $1$、$3$、$2$ 这样排列队伍,获得奖赏最多的大臣所获得金币数为 $2$;
按 $2$、$1$、$3$ 这样排列队伍,获得奖赏最多的大臣所获得金币数为 $2$;
按$ 2$、$3$、$1 $这样排列队伍,获得奖赏最多的大臣所获得金币数为 $9$;
按 $3$、$1$、$2 $这样排列队伍,获得奖赏最多的大臣所获得金币数为 $2$;
按$ 3$、$2$、$1$ 这样排列队伍,获得奖赏最多的大臣所获得金币数为 $9$。
因此,奖赏最多的大臣最少获得 $2$ 个金币,答案输出 $2$。
【数据范围】
对于 $20%$ 的数据,有 $1≤ n≤ 10,0 < a,b < 8$;
对于 $40%$ 的数据,有$ 1≤ n≤20,0 < a,b < 8$;
对于 $60%$ 的数据,有 $1≤ n≤100$;
对于 $60%$ 的数据,保证答案不超过 $10^9$;
对于 $100%$ 的数据,有 $1 ≤ n ≤1,000,0 < a,b < 10000$。
NOIP 2012 提高组 第一天 第二题
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define sf(x) scanf("%d", &x);
#define de(x) cout << x << " ";
#define Pu puts("");
const int N = 2e4 + 9, mod = 1e9 + 7;
int n, m;
int cheng[N], chu[N], ans[N];
struct E {
int l, r;
} e[N];
bool cmp(E a, E b) {
return (a.l * a.r < b.l * b.r);
}
void times(int x) { // 大数乘法
int t = 0;
for (int i = 1; i <= cheng[0]; i++) {
t = cheng[i] * x + t;
cheng[i] = t % 10;
t /= 10;
}
int id = cheng[0];
while (t) {
cheng[++id] = t % 10;
t /= 10;
}
cheng[0] = id;
}
void divition(int x) { // 大数除法(向下取整)
memset(chu, 0, sizeof(chu)); // 除数需要置为0
int t = 0;
for (int i = cheng[0]; i >= 1; i--) {
t = t * 10 + cheng[i];
chu[i] = t / x;
if (chu[0] == 0 && chu[i] != 0) {
chu[0] = i; // 如果当前商为0,并且得到的商不为0
// 此时i即为最后商的位数
}
t %= x;
}
}
bool compare() {
if (ans[0] == chu[0]) {
for (int i = chu[0]; i >= 1; i--) {
if (chu[i] > ans[i])
return 1;
if (chu[i] < ans[i]) {
return 0;
}
}
}
if (ans[0] < chu[0])
return 1;
if (ans[0] > chu[0]) {
return 0;
}
return -1;
}
void cp() {
ans[0] = chu[0];
for (int i = chu[0]; i >= 1; i--) {
ans[i] = chu[i];
}
}
int main() {
cin >> n;
n++;
for (int i = 1; i <= n; i++) {
cin >> e[i].l >> e[i].r;
}
sort(e + 2, e + n + 1, cmp); // 注意国王的位置不变
cheng[0] = 1; // 位数
cheng[1] = 1; // 因为是乘法,所以用1乘以其他的数
for (int i = 2; i <= n; i++) {
times(e[i - 1].l); // 乘以它前面人的左手数
divition(e[i].r); // 除以自己的右手数
if (compare()) { // 如果大于当前存储的最大值,则更换
cp();
}
}
for (int i = ans[0]; i >= 1; i--) {
printf("%d", ans[i]);
}
return 0;
}
【模板】队列
题目描述
请你实现一个队列(queue),支持如下操作:
push(x):向队列中加入一个数 $x$。pop():将队首弹出。如果此时队列为空,则不进行弹出操作,并输出ERR_CANNOT_POP。query():输出队首元素。如果此时队列为空,则输出ERR_CANNOT_QUERY。size():输出此时队列内元素个数。
输入格式
第一行,一个整数 $n$,表示操作的次数。
接下来 $n$ 行,每行表示一个操作。格式如下:
1 x,表示将元素x加入队列。2,表示将队首弹出队列。3,表示查询队首。4,表示查询队列内元素个数。
输出格式
输出若干行,对于每个操作,按「题目描述」输出结果。
每条输出之间应当用空行隔开。
样例 #1
样例输入 #1
13
1 2
3
4
1 233
3
2
3
2
4
3
2
1 144
3
样例输出 #1
2
1
2
233
0
ERR_CANNOT_QUERY
ERR_CANNOT_POP
144
提示
样例解释
首先插入 2,队首为 2、队列内元素个数为 1。
插入 233,此时队首为 2。
弹出队首,此时队首为 233。
弹出队首,此时队首为空。
再次尝试弹出队首,由于队列已经为空,此时无法弹出。
插入 144,此时队首为 144。
数据规模与约定
对于 $100%$ 的测试数据,满足 $n\leq 10000$,且被插入队列的所有元素值是 $[1, 1000000]$ 以内的正整数。
#include<iostream>
#include<queue>
using namespace std;
int x,op,n;
queue<int> q;
int main(){
cin>>n;
for(int i=1;i<=n;i++){
cin>>op;
if(op==1){
cin>>x;
q.push(x);//从队列里放入一个元素
}
if(op==2){
if(!q.empty()) q.pop();//如果队列不是空的,则将队首元素弹出
else cout<<"ERR_CANNOT_POP"<<endl;
}
if(op==3){
if(!q.empty()){
cout<<q.front()<<endl;//如果队列不是空的,则将队首元素输出
}
else{
cout<<"ERR_CANNOT_QUERY"<<endl;
}
}
if(op==4){
cout<<q.size()<<endl;//输出此时队列中的元素个数
}
}
return 0;
}
约瑟夫问题
题目描述
$n$ 个人围成一圈,从第一个人开始报数,数到 $m$ 的人出列,再由下一个人重新从 $1$ 开始报数,数到 $m$ 的人再出圈,依次类推,直到所有的人都出圈,请输出依次出圈人的编号。
注意:本题和《深入浅出-基础篇》上例题的表述稍有不同。书上表述是给出淘汰 $n-1$ 名小朋友,而该题是全部出圈。
输入格式
输入两个整数 $n,m$。
输出格式
输出一行 $n$ 个整数,按顺序输出每个出圈人的编号。
样例 #1
样例输入 #1
10 3
样例输出 #1
3 6 9 2 7 1 8 5 10 4
提示
$1 \le m, n \le 100$
#include<stdio.h>
int n,m,count=0;
int res[105]={0};
int main(){
scanf("%d%d",&n,&m);
for(int i=0;i<n;i++){//所有人都得出去
for(int j=0;j<m;j++){//叫号
//for循环中的两条语句不能更换顺序
if(++count>n) count=1;//如果叫过一轮,从头再叫
if(res[count]) j--;//如果此人已经出去,从头再叫
}
printf("%d ",count);
res[count]=1;//叫到的出去
}
return 0;
}
七海的简单计数问题
题目背景

众所周时,在原晓是个学渣,但他的妹妹在原七海是个学霸。最近马上就要考试了,七海给晓补习。
七海出了一个简单计数题给晓做,这个晓丑显然是做不出计数题的。七海还说晓做不出这个题之后就要做一个星期的饺子,但是晓一点都不想再吃饺子了。
趁着这会七海不在的功夫,晓丑把题目扔给了你,希望你能帮他算一下正确答案。
题目描述
给一个仅包含数字的字符串 $s$;问这个字符串中有多少个子串是七海字符串。
一个字符串是七海字符串当且仅当其含有子序列 773。
如果两个子串在原串中的位置不同,我们就认为这两个子串的是不同的。
输入格式
一行包含一个字符串 $s$;保证 $s$ 中只包含数字。
输出格式
一行一个非负整数代表答案。
样例 #1
样例输入 #1
77
样例输出 #1
0
样例 #2
样例输入 #2
773773
样例输出 #2
7
样例 #3
样例输入 #3
0773
样例输出 #3
2
样例 #4
样例输入 #4
773
样例输出 #4
1
提示
$|s| \leq 300000$
#include <iostream>
#include <cstdio>
using namespace std;
long long ans;
int ls, r = -1;
string s;
int a[20];
int main()
{
ios::sync_with_stdio(false);
cin >> s;
ls = s.length();
for (int l = 0; l < ls; l++) {
while (a[7] < 2 && r < ls) {
r++;
if (r < ls && (int)(s[r] - '0') == 7)
a[(int)(s[r]) - '0']++;
}
while (a[3] < 1 && r < ls) {
r++;
if (r < ls)
a[(int)(s[r] - '0')]++;
}
ans = ans + ls - r;
if ((int)(s[l] - '0') == 7)
a[(int)(s[l] - '0')]--;
if (a[7] < 2)
a[3] = 0;
}
cout << ans;
return 0;
}
【模板】栈
题目描述
请你实现一个栈(stack),支持如下操作:
push(x):向栈中加入一个数 $x$。pop():将栈顶弹出。如果此时栈为空则不进行弹出操作,输出Empty。query():输出栈顶元素,如果此时栈为空则输出Anguei!。size():输出此时栈内元素个数。
输入格式
本题单测试点内有多组数据。
输入第一行是一个整数 $T$,表示数据组数。对于每组数据,格式如下:
每组数据第一行是一个整数,表示操作的次数 $n$。
接下来 $n$ 行,每行首先由一个字符串,为 push,pop,query 和 size 之一。若为 push,则其后有一个整数 $x$,表示要被加入的数,$x$ 和字符串之间用空格隔开;若不是 push,则本行没有其它内容。
输出格式
对于每组数据,按照「题目描述」中的要求依次输出。每次输出占一行。
样例 #1
样例输入 #1
2
5
push 2
query
size
pop
query
3
pop
query
size
样例输出 #1
2
1
Anguei!
Empty
Anguei!
0
提示
样例 1 解释
对于第二组数据,始终为空,所以 pop 和 query 均需要输出对应字符串。栈的 size 为 0。
数据规模与约定
对于全部的测试点,保证 $1 \leq T, n\leq 10^6$,且单个测试点内的 $n$ 之和不超过 $10^6$,即 $\sum n \leq 10^6$。保证 $0 \leq x \lt 2^{64}$。
提示
- 请注意大量数据读入对程序效率造成的影响。
- 因为一开始数据造错了,请注意输出的
Empty不含叹号,Anguei!含有叹号。
#include <bits/stdc++.h>
using namespace std;
typedef unsigned long long ll;
const int N = 1e6 + 1;
class MyStack
{
private:
int i = 0;
ll nums[N];
public:
void push(ll x)
{
if (i < N)
{
nums[i++] = x;
}
}
void pop()
{
if (i > 0)
{
i--;
}
else
{
printf("Empty\n");
}
}
void query()
{
if (i > 0)
{
printf("%llu\n", nums[i - 1]);
}
else
{
printf("Anguei!\n");
}
}
void size()
{
printf("%d\n", i);
}
};
int main()
{
int t;
cin >> t;
while (t--)
{
int n;
scanf("%d", &n);
MyStack stack;
while (n--)
{
string ord;
cin >> ord;
if (ord == "push")
{
ll x;
scanf("%llu", &x);
stack.push(x);
}
else if (ord == "pop")
{
stack.pop();
}
else if (ord == "query")
{
stack.query();
}
else if (ord == "size")
{
stack.size();
}
}
}
return 0;
}
表达式括号匹配
题目描述
假设一个表达式有英文字母(小写)、运算符(+、-、*、/)和左右小(圆)括号构成,以 @ 作为表达式的结束符。请编写一个程序检查表达式中的左右圆括号是否匹配,若匹配,则输出 YES;否则输出 NO。表达式长度小于 $255$,左圆括号少于 $20$ 个。
输入格式
一行:表达式。
输出格式
一行:YES 或 NO。
样例 #1
样例输入 #1
2*(x+y)/(1-x)@
样例输出 #1
YES
样例 #2
样例输入 #2
(25+x)*(a*(a+b+b)@
样例输出 #2
NO
提示
表达式长度小于 $255$,左圆括号少于 $20$ 个。
#include <bits/stdc++.h>
using namespace std;
#define maxn 20;
char c[256];
bool judge (char c[256]){
int top=0,i=0;
while(c[i]!='@')
{
if(c[i]=='(') top++;
if(c[i]==')')
{
if(top>0) top--;
else return 0;
}
i++;
}
if(top!=0) return 0;
else return 1;
}
int main()
{
scanf("%s",c);
if(judge(c)) cout<<"YES";
else cout<<"NO";
return 0;
}
Longest Regular Bracket Sequence
题面翻译
给出一个括号序列,求出最长合法子串和它的数量。
合法的定义:这个序列中左右括号匹配
题目描述
This is yet another problem dealing with regular bracket sequences.
We should remind you that a bracket sequence is called regular, if by inserting «+» and «1» into it we can get a correct mathematical expression. For example, sequences «(())()», «()» and «(()(()))» are regular, while «)(», «(()» and «(()))(» are not.
You are given a string of «(» and «)» characters. You are to find its longest substring that is a regular bracket sequence. You are to find the number of such substrings as well.
输入格式
The first line of the input file contains a non-empty string, consisting of «(» and «)» characters. Its length does not exceed $ 10^{6} $ .
输出格式
Print the length of the longest substring that is a regular bracket sequence, and the number of such substrings. If there are no such substrings, write the only line containing "0 1".
样例 #1
样例输入 #1
)((())))(()())
样例输出 #1
6 2
样例 #2
样例输入 #2
))(
样例输出 #2
0 1
#include <iostream>
#include <cstring>
#include <stack>
#include <cstdio>
using namespace std;
const int N = 1e6+5;
char s[N];
int d[N],c[N]; // d[i]代表与i匹配的左括号的坐标,c[i]代表这个序列的最左边
int main()
{
scanf("%s",s);
int len = strlen(s);
stack<int> a; //存的是左括号的坐标
for(int i = 0 ;i < len ; i++){
if(s[i] == '('){
a.push(i);
}
else{
if(a.empty()){
d[i] = -1;
c[i] = -1;
}
else{
d[i] = a.top();
a.pop();
c[i] = d[i];
if(d[i] > 0 && s[d[i]-1] == ')' && c[d[i]-1] != -1){
c[i] = c[d[i]-1];
}
}
}
}
int ans = 0,cnt = 0;
for(int i = 0 ; i < len;i++){
if(c[i] != -1 && s[i] == ')'){
if(i - c[i] + 1 > ans) {
ans = i - c[i] + 1;
cnt = 1;
}
else if(i - c[i] + 1 == ans){
cnt ++;
}
}
}
if(ans == 0) cout << 0 << " " << 1 << endl;
else cout << ans << " " << cnt << endl;
return 0;
}
全排列问题
题目描述
按照字典序输出自然数 $1$ 到 $n$ 所有不重复的排列,即 $n$ 的全排列,要求所产生的任一数字序列中不允许出现重复的数字。
输入格式
一个整数 $n$。
输出格式
由 $1 \sim n$ 组成的所有不重复的数字序列,每行一个序列。
每个数字保留 $5$ 个场宽。
样例 #1
样例输入 #1
3
样例输出 #1
1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1
提示
$1 \leq n \leq 9$。
#include<bits/stdc++.h>
using namespace std;
bool vis[15];//vis[i]=1,表示数字i已经被占用,此后步骤不能填写数字i,以防数字被重复使用
int a[15],n;
void dfs(int k){
if(k==n+1){
for(int i=1;i<=n;i++){
cout<<setw(5)<<a[i];
}
cout<<endl;
return;
}
for(int i=1;i<=n;i++){
if(vis[i]==true)continue;
a[k]=i;
vis[i]=true;
dfs(k+1);
a[k]=0;
vis[i]=false;
}
}
int main(){
cin>>n;
dfs(1);
return 0;
}
[USACO1.5] 八皇后 Checker Challenge
题目描述
一个如下的 $6 \times 6$ 的跳棋棋盘,有六个棋子被放置在棋盘上,使得每行、每列有且只有一个,每条对角线(包括两条主对角线的所有平行线)上至多有一个棋子。

上面的布局可以用序列 $2\ 4\ 6\ 1\ 3\ 5$ 来描述,第 $i$ 个数字表示在第 $i$ 行的相应位置有一个棋子,如下:
行号 $1\ 2\ 3\ 4\ 5\ 6$
列号 $2\ 4\ 6\ 1\ 3\ 5$
这只是棋子放置的一个解。请编一个程序找出所有棋子放置的解。
并把它们以上面的序列方法输出,解按字典顺序排列。
请输出前 $3$ 个解。最后一行是解的总个数。
输入格式
一行一个正整数 $n$,表示棋盘是 $n \times n$ 大小的。
输出格式
前三行为前三个解,每个解的两个数字之间用一个空格隔开。第四行只有一个数字,表示解的总数。
样例 #1
样例输入 #1
6
样例输出 #1
2 4 6 1 3 5
3 6 2 5 1 4
4 1 5 2 6 3
4
提示
【数据范围】
对于 $100%$ 的数据,$6 \le n \le 13$。
题目翻译来自NOCOW。
USACO Training Section 1.5
#include <iostream>
#include <cmath>
#include <memory.h>
#include <algorithm>
using namespace std;
int ans[115]={0},n,k;
int a[110],b[110],c[110],d[110],m,l;//用a数组记录皇后可以占领的位置,b数组表示已被使用过的列,c,d数组表示两个对角线
void dfs(int ci,int cnt)//ci为行,cnt记录皇后占领位置的个数
{
if(cnt==n)
{
if(m>=3)//只需要求出前三种
{
m++;return;//持续计数
}
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
if(a[j]==i)//从记录的a数组中把找出来的点按顺序放入答案数组中
ans[l++]=j;
m++;//计数
return;
}
for(int i=1;i<=n;i++)
{
if((!b[i])&&(!c[ci+i])&&(!d[ci-i+n]))
{
a[i]=ci;
b[i]=1;
c[ci+i]=1;
d[ci-i+n]=1;//用几个数组统一表示行和列和对角线,对比在”地图“中一个个位置去标记,大大节省了时间复杂度
dfs(ci+1,cnt+1);
a[i]=0;
b[i]=0;
c[ci+i]=0;
d[ci-i+n]=0;//回溯
}
}
}
int main()
{
scanf("%d",&n);
dfs(1,0);
for(int i=0;i<l;i++)
{
printf("%d ",ans[i]);
if((i+1)%n==0)
printf("\n");
}
cout <<m;
}
取数游戏
题目描述
一个 $N\times M$ 的由非负整数构成的数字矩阵,你需要在其中取出若干个数字,使得取出的任意两个数字不相邻(若一个数字在另外一个数字相邻 $8$ 个格子中的一个即认为这两个数字相邻),求取出数字和最大是多少。
输入格式
第一行有一个正整数 $T$,表示了有 $T$ 组数据。
对于每一组数据,第一行有两个正整数 $N$ 和 $M$,表示了数字矩阵为 $N$ 行 $M$ 列。
接下来 $N$ 行,每行 $M$ 个非负整数,描述了这个数字矩阵。
输出格式
共 $T$ 行,每行一个非负整数,输出所求得的答案。
样例 #1
样例输入 #1
3
4 4
67 75 63 10
29 29 92 14
21 68 71 56
8 67 91 25
2 3
87 70 85
10 3 17
3 3
1 1 1
1 99 1
1 1 1
样例输出 #1
271
172
99
提示
样例解释
对于第一组数据,取数方式如下:
$$\begin{matrix}
[67] & 75 & 63 & 10 \
29 & 29 & [92] & 14 \
[21] & 68 & 71 & 56 \
8 & 67 & [91] & 25 \
\end{matrix}$$
数据范围及约定
- 对于$20%$的数据,$1\le N, \le 3$;
- 对于$40%$的数据,$1\le N,M\le 4$;
- 对于$60%$的数据,$1\le N, \le 5$;
- 对于$100%$的数据,$1\le N, M\le 6$,$1\le T\le 20$。
#include<bits/stdc++.h>//万能头文件
using namespace std;
const int d[8][2]={1,0,-1,0,0,1,0,-1,1,1,-1,1,1,-1,-1,-1};//方向数组用来控制搜索时的方向
int t,n,m,s[8][8],mark[8][8],ans,mx;
void dfs(int x,int y){//搜索函数,表示搜索点(x,y)
if(y==m+1){//当y到边界时,搜索下一行
dfs(x+1,1);
return;
}
if(x==n+1){//当x到边界时,搜索结束,刷新最大值
mx=max(ans,mx);
return;
}
dfs(x,y+1);// 不取此数的情况
if(mark[x][y]==0){ //取此数的情况(需保证此数周围没有取其他数,即mark[i][j]==0)
ans+=s[x][y];
for(int fx=0;fx<8;++fx){ //标记周围的数
++mark[x+d[fx][0]][y+d[fx][1]];
}
dfs(x,y+1);
for(int fx=0;fx<8;++fx){ //回溯
--mark[x+d[fx][0]][y+d[fx][1]];
}
ans-=s[x][y];
}
}
int main(){
cin>>t;
while(t--){
memset(s,0,sizeof(s));
memset(mark,0,sizeof(mark));//在做每个数据前都要初始化数组
cin>>n>>m;
for(int i=1;i<=n;++i){
for(int j=1;j<=m;++j){
cin>>s[i][j];
}
}
mx=0;
dfs(1,1);//从点(1,1)开始搜索
printf("%d\n",mx);//输出答案
}
return 0;
}
高手去散步
题目背景
高手最近谈恋爱了。不过是单相思。“即使是单相思,也是完整的爱情”,高手从未放弃对它的追求。今天,这个阳光明媚的早晨,太阳从西边缓缓升起。于是它找到高手,希望在晨读开始之前和高手一起在鳌头山上一起散步。高手当然不会放弃这次梦寐以求的机会,他已经准备好了一切。
题目描述
鳌头山上有 $n$ 个观景点,观景点两两之间有游步道共 $m$ 条。高手的那个它,不喜欢太刺激的过程,因此那些没有路的观景点高手是不会选择去的。另外,她也不喜欢去同一个观景点一次以上。而高手想让他们在一起的路程最长(观景时它不会理高手),已知高手的穿梭机可以让他们在任意一个观景点出发,也在任意一个观景点结束。
输入格式
第一行,两个用空格隔开的整数 $n$ 、 $m.$ 之后 $m$ 行,为每条游步道的信息:两端观景点编号、长度。
输出格式
一个整数,表示他们最长相伴的路程。
样例 #1
样例输入 #1
4 6
1 2 10
2 3 20
3 4 30
4 1 40
1 3 50
2 4 60
样例输出 #1
150
提示
对于 $100%$ 的数据:$n \le 20$,$m \le 50$,保证观景点两两之间不会有多条游步道连接。
#include<bits/stdc++.h>
using namespace std;
const int N=110;
int n,m,flag;
int e[N],ne[N],h[N],w[N],idx;
int st[N];
int ans=-1e13;
void add(int a,int b,int c)
{
e[idx]=b,w[idx]=c,ne[idx]=h[a],h[a]=idx++;
}
void dfs(int u,int dis,int last)
{
// printf("%d %d\n",u,dis);
flag=0;
for(int i=h[last];i!=-1;i=ne[i])
{
int j=e[i];
if(st[j]==0)
flag=1;
}
if(flag==0)
{
ans=max(ans,dis);
return;
}
for(int i=h[last];i!=-1;i=ne[i])
{
int j=e[i];
if(st[j])continue;
st[j]=1;
dfs(u+1,dis+w[i],j);
st[j]=0;
}
}
int main()
{
memset(h,-1,sizeof h);
scanf("%d %d",&n,&m);
while(m--)
{
int a,b,c;
scanf("%d %d %d",&a,&b,&c);
add(a,b,c),add(b,a,c);
}
for(int i=1;i<=n;i++)
{
memset(st,0,sizeof st);
st[i]=1;//标记
dfs(0,0,i);
}
printf("%d\n",ans);
}
新二叉树
题目描述
输入一串二叉树,输出其前序遍历。
输入格式
第一行为二叉树的节点数 $n$。($1 \leq n \leq 26$)
后面 $n$ 行,每一个字母为节点,后两个字母分别为其左右儿子。特别地,数据保证第一行读入的节点必为根节点。
空节点用 * 表示
输出格式
二叉树的前序遍历。
样例 #1
样例输入 #1
6
abc
bdi
cj*
d**
i**
j**
样例输出 #1
abdicj
#include<bits/stdc++.h>
using namespace std;
struct MyStruct
{
char l, r; //左节点 右节点
}tree[200];
void dfs(char pos)
{
cout << pos;
if (tree[pos].l != '*') dfs(tree[pos].l);
if (tree[pos].r != '*') dfs(tree[pos].r);
}
int main()
{
int n;
char a, l, r, bg;
cin >> n;
cin >> bg >> l >> r;
tree[bg].l = l;
tree[bg].r = r;
for (int i = 0; i < n - 1; i++)
{
cin >> a >> l >> r;
tree[a].l = l;
tree[a].r = r;
}
dfs(bg);
return 0;
}
【深基16.例3】二叉树深度
题目描述
有一个 $n(n \le 10^6)$ 个结点的二叉树。给出每个结点的两个子结点编号(均不超过 $n$),建立一棵二叉树(根节点的编号为 $1$),如果是叶子结点,则输入 0 0。
建好这棵二叉树之后,请求出它的深度。二叉树的深度是指从根节点到叶子结点时,最多经过了几层。
输入格式
第一行一个整数 $n$,表示结点数。
之后 $n$ 行,第 $i$ 行两个整数 $l$、$r$,分别表示结点 $i$ 的左右子结点编号。若 $l=0$ 则表示无左子结点,$r=0$ 同理。
输出格式
一个整数,表示最大结点深度。
样例 #1
样例输入 #1
7
2 7
3 6
4 5
0 0
0 0
0 0
0 0
样例输出 #1
4
#include <iostream>
#include <cstdio>
using namespace std;
struct node {
int val, left, right;
}n[1001000];
int N, root = 0, maxLevel = 0;
bool isroot[1001000] = {0};
void dfs(int root, int level) {
maxLevel = max(maxLevel, level);
if(n[root].left != 0) dfs(n[root].left, level + 1);
if(n[root].right != 0) dfs(n[root].right, level + 1);
}
int main() {
scanf("%d", &N);
for(int i = 1; i <= N; i++) {
scanf("%d%d", &n[i].left, &n[i].right);
isroot[n[i].left] = isroot[n[i].right] = 1;
}
while(isroot[root]) root++;
dfs(root, 1);
printf("%d", maxLevel);
return 0;
}
最大子树和
题目描述
小明对数学饱有兴趣,并且是个勤奋好学的学生,总是在课后留在教室向老师请教一些问题。一天他早晨骑车去上课,路上见到一个老伯正在修剪花花草草,顿时想到了一个有关修剪花卉的问题。于是当日课后,小明就向老师提出了这个问题:
一株奇怪的花卉,上面共连有 $N$ 朵花,共有 $N-1$ 条枝干将花儿连在一起,并且未修剪时每朵花都不是孤立的。每朵花都有一个“美丽指数”,该数越大说明这朵花越漂亮,也有“美丽指数”为负数的,说明这朵花看着都让人恶心。所谓“修剪”,意为:去掉其中的一条枝条,这样一株花就成了两株,扔掉其中一株。经过一系列“修剪“之后,还剩下最后一株花(也可能是一朵)。老师的任务就是:通过一系列“修剪”(也可以什么“修剪”都不进行),使剩下的那株(那朵)花卉上所有花朵的“美丽指数”之和最大。
老师想了一会儿,给出了正解。小明见问题被轻易攻破,相当不爽,于是又拿来问你。
输入格式
第一行一个整数 $n\ (1\le N\le 16000)$。表示原始的那株花卉上共 $n$ 朵花。
第二行有 $n$ 个整数,第 $i$ 个整数表示第 $i$ 朵花的美丽指数。
接下来 $n-1$ 行每行两个整数 $a,b$,表示存在一条连接第 $a$ 朵花和第 $b$ 朵花的枝条。
输出格式
一个数,表示一系列“修剪”之后所能得到的“美丽指数”之和的最大值。保证绝对值不超过 $2147483647$。
样例 #1
样例输入 #1
7
-1 -1 -1 1 1 1 0
1 4
2 5
3 6
4 7
5 7
6 7
样例输出 #1
3
提示
数据范围及约定
- 对于 $60%$ 的数据,有 $1\le N\le 1000$;
- 对于 $100%$ 的数据,有 $1\le N\le 16000$。
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<iostream>
#include<queue>
using namespace std;
const int N=1e5+10;
int h[N],e[N],ne[N],idx;
int f[N],ans;//f[i]表示以i为根的子树中的最大美丽指数
void add(int x,int y)
{
e[idx]=y;
ne[idx]=h[x];
h[x]=idx++;
}
void dfs(int x,int fa)
{
for(int i=h[x];i!=-1;i=ne[i])
{
int j=e[i];
if(j==fa) continue;
dfs(j,x);
if(f[j]>0) f[x]+=f[j];
}
ans=max(ans,f[x]);
}
int main()
{
int n;
cin>>n;
memset(h,-1,sizeof h);
for(int i=1;i<=n;i++)
scanf("%d",&f[i]);
for(int i=1;i<n;i++)
{
int u,v;
scanf("%d%d",&u,&v);
add(u,v);add(v,u);
}
ans=-0x3f3f3f3f;
dfs(1,-1);
printf("%d",ans);
return 0;
}
[USACO3.4] 美国血统 American Heritage
题目描述
农夫约翰非常认真地对待他的奶牛们的血统。然而他不是一个真正优秀的记帐员。他把他的奶牛 们的家谱作成二叉树,并且把二叉树以更线性的“树的中序遍历”和“树的前序遍历”的符号加以记录而 不是用图形的方法。
你的任务是在被给予奶牛家谱的“树中序遍历”和“树前序遍历”的符号后,创建奶牛家谱的“树的 后序遍历”的符号。每一头奶牛的姓名被译为一个唯一的字母。(你可能已经知道你可以在知道树的两 种遍历以后可以经常地重建这棵树。)显然,这里的树不会有多于 $26$ 个的顶点。
这是在样例输入和样例输出中的树的图形表达方式:
C
/ \
/ \
B G
/ \ /
A D H
/ \
E F
附注:
- 树的中序遍历是按照左子树,根,右子树的顺序访问节点;
- 树的前序遍历是按照根,左子树,右子树的顺序访问节点;
- 树的后序遍历是按照左子树,右子树,根的顺序访问节点。
输入格式
第一行一个字符串,表示该树的中序遍历。
第二行一个字符串,表示该树的前序遍历。
输出格式
单独的一行表示该树的后序遍历。
样例 #1
样例输入 #1
ABEDFCHG
CBADEFGH
样例输出 #1
AEFDBHGC
提示
题目翻译来自NOCOW。
USACO Training Section 3.4
#include <iostream>
#define Max 50
using namespace std;
typedef struct Node {
char x;
Node *left;
Node *right;
}*node;
Node a[Max];
string mid_str,pre_str;
void pos_print(node root);
Node *get_root(int preL,int preR,int midL,int midR);//先序遍历范围,中序遍历的范围
int main()
{
cin>>mid_str>>pre_str;
node root=get_root(0,pre_str.size()-1,0,pre_str.size()-1);
pos_print(root);
}
Node *get_root(int preL,int preR,int midL,int midR)//先序遍历范围,中序遍历的范围
{
if(preL>preR)
{
return NULL;
}
node root=new Node;
root->x=pre_str[preL];
int i;
for(i=midL;i<=midR;i++)
{
if(mid_str[i]==pre_str[preL])
{
break;//找到了根节点
}
}
int num=i-midL;//左子树的节点个数
root->left=get_root(preL+1,preL+num,midL,i-1);
root->right=get_root(preL+num+1,preR,i+1,midR);
return root;
}
void pos_print(node root)
{
if(root!=NULL)
{
pos_print(root->left);
pos_print(root->right);
cout<<root->x;
}
}
医院设置
题目描述
设有一棵二叉树,如图:
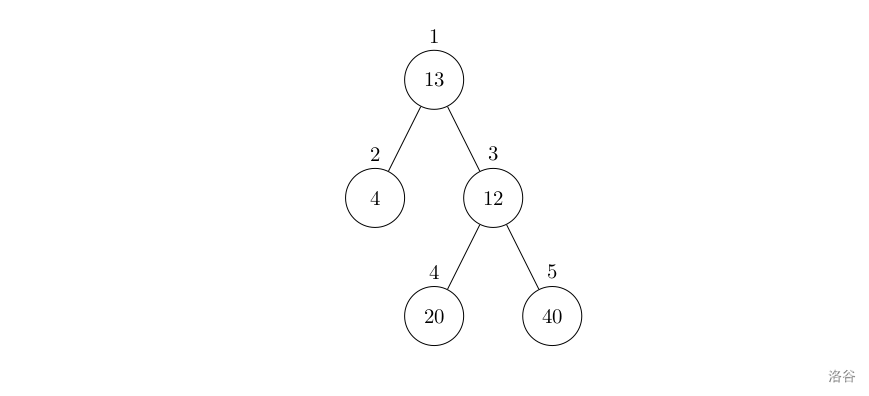
其中,圈中的数字表示结点中居民的人口。圈边上数字表示结点编号,现在要求在某个结点上建立一个医院,使所有居民所走的路程之和为最小,同时约定,相邻接点之间的距离为 $1$。如上图中,若医院建在 $1$ 处,则距离和 $=4+12+2\times20+2\times40=136$;若医院建在 $3$ 处,则距离和 $=4\times2+13+20+40=81$。
输入格式
第一行一个整数 $n$,表示树的结点数。
接下来的 $n$ 行每行描述了一个结点的状况,包含三个整数 $w, u, v$,其中 $w$ 为居民人口数,$u$ 为左链接(为 $0$ 表示无链接),$v$ 为右链接(为 $0$ 表示无链接)。
输出格式
一个整数,表示最小距离和。
样例 #1
样例输入 #1
5
13 2 3
4 0 0
12 4 5
20 0 0
40 0 0
样例输出 #1
81
提示
数据规模与约定
对于 $100%$ 的数据,保证 $1 \leq n \leq 100$,$0 \leq u, v \leq n$,$1 \leq w \leq 10^5$。
#include<stdio.h>
struct node
{
int father,left,right,value;
}t[105];
int sum=999999,ans=999999,vis[105];
int min(int a,int b)
{
if(a>b) return b;
else return a;
}
void dfs(int step,int pos)
{
int i,f,l,r;
sum+=step*t[pos].value;
f=t[pos].father;l=t[pos].left;r=t[pos].right;
if(f&&!vis[f])
{
vis[f]=1;
dfs(step+1,f);
}
if(l&&!vis[l])
{
vis[l]=1;
dfs(step+1,l);
}
if(r&&!vis[r])
{
vis[r]=1;
dfs(step+1,r);
}
}
main()
{
int n,i,j;
scanf("%d",&n);
for(i=1;i<=n;i++)
{
scanf("%d %d %d",&t[i].value,&t[i].left,&t[i].right);
t[t[i].left].father=t[t[i].right].father=i;
}
for(i=1;i<=n;i++)
{
sum=0;
for(j=0;j<=105;j++)
vis[j]=0;
vis[i]=1;
dfs(0,i);
ans=min(sum,ans);
//printf("%d\n",ans);
}
printf("%d",ans);
}
[POI2008] STA-Station
题目描述
给定一个 $n$ 个点的树,请求出一个结点,使得以这个结点为根时,所有结点的深度之和最大。
一个结点的深度之定义为该节点到根的简单路径上边的数量。
输入格式
第一行有一个整数,表示树的结点个数 $n$。
接下来 $(n - 1)$ 行,每行两个整数 $u, v$,表示存在一条连接 $u, v$ 的边。
输出格式
本题存在 Special Judge。
输出一行一个整数表示你选择的结点编号。如果有多个结点符合要求,输出任意一个即可。
样例 #1
样例输入 #1
8
1 4
5 6
4 5
6 7
6 8
2 4
3 4
样例输出 #1
7
提示
样例 1 解释
输出 $7$ 和 $8$ 都是正确答案。
数据规模与约定
对于全部的测试点,保证 $1 \leq n \leq 10^6$,$1 \leq u, v \leq n$,给出的是一棵树。
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1000010;
long long head[maxn],n,cnt,size[maxn],f[maxn],depth[maxn];
struct node{
int to,pre;
}G[maxn<<1];
void addedge(int from,int to){
G[++cnt].to = to;
G[cnt].pre = head[from];
head[from] = cnt;
}
void dfs1(int u,int fa){
size[u] = 1;
depth[u] = depth[fa] + 1;
for(int i = head[u];i;i = G[i].pre){
int v = G[i].to;
if(v == fa) continue;
dfs1(v,u);
size[u] += size[v];
}
}
void dfs2(int u,int fa){
for(int i = head[u];i;i = G[i].pre){
int v = G[i].to;
if(v == fa) continue;
f[v] = f[u] + n - 2 * size[v];
dfs2(v,u);
}
}
int main(){
int x,y;
long long ans,tmp;
scanf("%d",&n);
for(int i = 1;i < n;i++){
scanf("%d%d",&x,&y);
addedge(x,y);addedge(y,x);
}
dfs1(1,0);
for(int i = 1;i <= n;i++) f[1] += depth[i];
dfs2(1,0);
for(int i = 1;i <= n;i++){
if(f[i] > ans) ans = f[i],tmp = i;
}
printf("%lld\n",tmp);
return 0;
}
统计数字字符个数
题目描述
输入一行字符,统计出其中数字字符的个数。
输入格式
一行字符串,总长度不超过 $255$。
输出格式
输出为 $1$ 行,输出字符串里面数字字符的个数。
样例 #1
样例输入 #1
Today is 2021-03-27
样例输出 #1
8
#include<stdio.h>
#include<math.h>
#include<string.h>
#include<stdlib.h>
#include<stdbool.h>
int main(){
char c;
int i,sum=0,n;
while(scanf("%c",&c)!=EOF){
if(c>='0'&&c<='9'){
sum++;
}
}
printf("%d\n",sum);
return 0;
}
输出亲朋字符串
题目描述
亲朋字符串定义如下:给定字符串 $s$ 的第一个字符的 ASCII 值加第二个字符的 ASCII 值,得到第一个亲朋字符;$s$ 的第二个字符加第三个字符得到第二个亲朋字符;依此类推。注意:亲朋字符串的最后一个字符由 $s$ 的最后一个字符 ASCII 值加 $s$ 的第一个字符的 ASCII 值。
输入格式
输入一行,一个长度大于等于 $2$,小于等于 $100$ 的字符串。
输出格式
输出一行,为变换后的亲朋字符串。输入保证变换后的字符串只有一行。
样例 #1
样例输入 #1
1234
样例输出 #1
cege
#include<iostream>
#include<cstring>
using namespace std;
int main(){
ios::sync_with_stdio(false);//缩短cin进行读入所需的时间
char c[110],a[110];
cin>>a;
int i=0,k=0;
int len=strlen(a);
for(i=0;i<len-1;i++){
c[i]=a[i]+a[i+1];
}
c[i]=a[i]+a[0];
for(int j=0;j<len;j++)
cout<<c[j];
return 0;
}
[语言月赛 202307] 扶苏和串
题目背景
众所周知,每个月入门赛的字符串题都是扶苏来枚举 idea 出出来的。
题目描述
给定一个 01 字符串 $s$,你可以任选 $s$ 的一个非空子串,把这个子串在 $s$ 中翻转一次。
问你能得到字典序最小的字符串是什么?
形式化的,你可以选择一个区间 $[l, r]$ 满足 $1 \leq l \leq r \leq |s|$,构造一个串 $t$ 满足:
$$t_i = \begin{cases}s_i, &i < l \text{ 或 } i > r \ s_{r - (i - l)}, & l \leq i \leq r\end{cases}$$
这里字符串的下标从 $1$ 开始。
最小化字符串 $t$ 的字典序。
输入格式
输入只有一行一个字符串,表示 $s$。
输出格式
输出一行一个字符串,表示得到的字典序最小的字符串。
样例 #1
样例输入 #1
101
样例输出 #1
011
样例 #2
样例输入 #2
0010100
样例输出 #2
0000101
提示
样例 1 解释
$s = \texttt{\underline{10}1}$,翻转下划线标出的子串,得到 $t = \texttt{011}$
样例 2 解释
$s = \texttt{00\underline{10100}}$,翻转下划线标出的子串,得到 $\texttt{0000101}$。
数据规模与约定
下面用 $|s|$ 表示输入字符串的长度。
- 对 $20%$ 的数据,$|s| \leq 2$。
- 对 $40%$ 的数据,$|s| \leq 8$。
- 另有 $10%$ 的数据,$s$ 只含字符 $\texttt 1$。
- 另有 $10%$ 的数据,$s$ 只含字符 $\texttt 0$。
- 对 $100%$ 的数据,$1 \leq |s| \leq 100$。$s$ 只含字符 $\texttt{0,1}$。
#include <bits/stdc++.h>
using namespace std;
string s, s1, ans;
int l, x, y = 0, c[3000];
int main(){
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
cin >> s;
ans = s;
l = s.size();
for (int i = 0; i < l; i++){
if (s[i] == '1'){
x = i;
break;
}
}
for (int i = x; i < l; i++){
if (s[i] == '0'){
c[i] = c[i - 1] + 1;
} else {
c[i] = 0;
}
if (c[i] >= c[y]){
y = i;
s1 = s;
int u = x, v = y;
while (u <= v){
swap(s1[u], s1[v]);
u++;
v--;
}
for (int j = 0; j < l; j++){
if (s1[j] < ans[j]){
ans = s1;
break;
} else if (s1[j] > ans[j]){
break;
}
}
}
}
cout << ans;
return 0;
}
[蓝桥杯 2020 国 C] 重复字符串
题目描述
如果一个字符串 $S$ 恰好可以由某个字符串重复 $K$ 次得到,我们就称 $S$ 是 $K$ 次重复字符串。例如 abcabcabc 可以看作是 abc 重复 $3$ 次得到,所以 abcabcabc 是 $3$ 次重复字符串。
同理 aaaaaa 既是 $2$ 次重复字符串、又是 $3$ 次重复字符串和 $6$ 次重复字符串。
现在给定一个字符串 $S$,请你计算最少要修改其中几个字符,可以使 $S$ 变为一个 $K$ 次字符串?
输入格式
输入第一行包含一个整数 $K$。
第二行包含一个只含小写字母的字符串 $S$。
输出格式
输出一个整数代表答案。如果 $S$ 无法修改成 $K$ 次重复字符串,输出 $−1$。
样例 #1
样例输入 #1
2
aabbaa
样例输出 #1
2
提示
其中,$1 \le K \le 10^5$,$1 \le |S| \le 10^5$。其中 $∣S∣$ 表示 $S$ 的 长度。
蓝桥杯 2020 年国赛 C 组 G 题。
#include<iostream>
#include<cstring>
#include<cstdio>
using namespace std;
int k,len,cir,ans,maxn,sum[1005];
string s;
int main(){
cin>>k>>s; //输入。
len=s.length(); //字符串长度。
cir=len/k; //循环节长度。
if(len%k!=0){ //判断是否可以分成K个循环节。
cout<<-1<<endl;
return 0;
}
for(int i=0;i<len/k;i++){ //因为下标加上循环节长度不能超过总长度,所以是len/k。
memset(sum,0,sizeof(sum)); //初始化桶。
maxn=0; //最大值归零。
for(int j=i;j<len;j+=cir){
sum[s[j]]++; //累加桶。
}
for(char c='a';c<='z';c++){
maxn=max(maxn,sum[c]); //比较选择最大值。
}
ans+=(k-maxn); //其余字符改动次数累加。
}
cout<<ans<<endl; //输出。
return 0;
}
[传智杯 #3 决赛] 子串
题目背景
disangan233 喜欢字符串,于是 disangan333 想让你找一些 disangan233 喜欢的串。
题目描述
在传智的开发课堂上,希望您开发一款文档处理软件。
给定 $T$ 组询问,每次给定 $2$ 个长度为 $n,m$ 的只含英文字母的字符串 $a,b$,求 $a$ 在 $b$ 中的出现次数,相同字符不区分大小写。注意 $a$ 是 $b$ 中连续子序列。
对于所有数据,$T\leq 100$,$\sum n\leq \sum m\leq 10^3$。字符串仅由大小或者小写的英文字母组成。
输入格式
输入共 $3T+1$ 行。
第 $1$ 行输入 $1$ 个正整数 $T$。
接下来共 $T$ 组输入,每组输入共 $3$ 行。
第 $1$ 行输入 $2$ 个正整数 $n,m$。
第 $2$ 行输入一个长度为 $n$ 的字符串 $a$。
第 $3$ 行输入一个长度为 $m$ 的字符串 $b$。
输出格式
输出共 $T$ 行,第 $i$ 行输出 $1$ 个整数,表示询问 $i$ 的答案。
样例 #1
样例输入 #1
5
3 10
abc
abcabcabca
2 10
aa
AAaAaaAaAa
5 5
AbCdE
eDcBa
5 5
abcde
ABCDE
3 10
aba
ABaBaAbaBA
样例输出 #1
3
9
0
1
4
提示
对于第一组输入,出现了 $3$ 次,分别是 [abc]abcabca,abc[abc]abca,abcabc[abc]a;
对于第二组输入,出现了 $9$ 次,分别是 [Aa]AaaAaAa,A[aA]aaAaAa,Aa[Aa]aAaAa,AaA[aa]AaAa,AaAa[aA]aAa,AaAaa[Aa]Aa,AaAaaA[aA]a,AaAaaA[aA]a,AaAaaAa[Aa]。
#include <iostream>
#include <string>
using namespace std;
string bsm(string s){
int l=s.size();
for(int i=0;i<l;i++){
if(s[i]>='A'&&s[i]<='Z')s[i]+=32;
}
return s;
}
int main(){
int t;
scanf("%d",&t);
while(t--){
int m,n,ans=0;
string a,b;
scanf("%d%d",&m,&n);
cin>>a>>b;
a= bsm(a),b= bsm(b);
for(int i=0;i<b.size();i++){
if(b.substr(i,a.size())==a){
ans++;
}
}
printf("%d\n",ans);
}
}
【模板】KMP
题目描述
给出两个字符串 $s_1$ 和 $s_2$,若 $s_1$ 的区间 $[l, r]$ 子串与 $s_2$ 完全相同,则称 $s_2$ 在 $s_1$ 中出现了,其出现位置为 $l$。
现在请你求出 $s_2$ 在 $s_1$ 中所有出现的位置。
定义一个字符串 $s$ 的 border 为 $s$ 的一个非 $s$ 本身的子串 $t$,满足 $t$ 既是 $s$ 的前缀,又是 $s$ 的后缀。
对于 $s_2$,你还需要求出对于其每个前缀 $s'$ 的最长 border $t'$ 的长度。
输入格式
第一行为一个字符串,即为 $s_1$。
第二行为一个字符串,即为 $s_2$。
输出格式
首先输出若干行,每行一个整数,按从小到大的顺序输出 $s_2$ 在 $s_1$ 中出现的位置。
最后一行输出 $|s_2|$ 个整数,第 $i$ 个整数表示 $s_2$ 的长度为 $i$ 的前缀的最长 border 长度。
样例 #1
样例输入 #1
ABABABC
ABA
样例输出 #1
1
3
0 0 1
提示
样例 1 解释
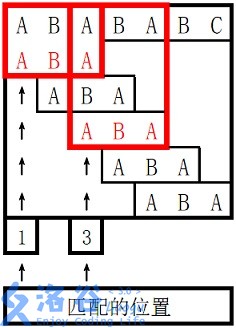 。
。
对于 $s_2$ 长度为 $3$ 的前缀 ABA,字符串 A 既是其后缀也是其前缀,且是最长的,因此最长 border 长度为 $1$。
数据规模与约定
本题采用多测试点捆绑测试,共有 3 个子任务。
- Subtask 1(30 points):$|s_1| \leq 15$,$|s_2| \leq 5$。
- Subtask 2(40 points):$|s_1| \leq 10^4$,$|s_2| \leq 10^2$。
- Subtask 3(30 points):无特殊约定。
对于全部的测试点,保证 $1 \leq |s_1|,|s_2| \leq 10^6$,$s_1, s_2$ 中均只含大写英文字母。
#include <iostream>
#include <string>
#define int long long
using namespace std;
const int N = 1000005;
int nxt[N], p, e;
string s1, s2;
signed main() {
cin >> s1 >> s2;
int ls1 = s1.size(), ls2 = s2.size();
for (int e = 1; e < ls2; e++) {
if (s2[p] == s2[e]) {
p++;
nxt[e] = p;
}
else {
while (nxt[p - 1] && s2[nxt[p - 1]] != s2[e])
p = nxt[p - 1];
if (s2[nxt[p - 1]] == s2[e]) {
p = nxt[p - 1] + 1;
nxt[e] = p;
}
else {
p = 0;
nxt[e] = p;
}
}
}
int j = 0;
for (int i = 0; i < ls1; i++) {
while (j != 0 && s1[i] != s2[j])
j = nxt[j - 1];
if (s1[i] == s2[j])
j++;
if (j == ls2) {
cout << i - ls2 + 2 << endl;
j = nxt[j - 1];
}
}
for (int i = 0; i < ls2; i++)
cout << nxt[i] << " ";
cout << endl;
return 0;
}
赵神牛的游戏
题目描述
在 DNF 中,赵神牛有一个缔造者,他一共有 $k$ 点法力值,一共有 $m$ 个技能,每个技能耗费的法力值为 $a_i$,可以造成的伤害为 $b_i$,而 boss 的体力值为 $n$,请你求出它放哪个技能,才可以打死 boss。
当然,赵神牛技术很菜,他一局只放一个技能,不过每个技能都可以放无数次。
输入格式
第一行有三个整数,分别表示 $k,m,n$。
后面 $m$ 行,每行两个整数,第 $(i + 1)$ 行的整数表示耗费的法力值 $a_i$ 和造成的伤害 $b_i$。
输出格式
输出仅一行,即可以杀死 boss 的技能序号,如果有多个,按从小到大的顺序输出,中间用一个空格隔开;如果没有技能能杀死 boss,输出 -1。
样例 #1
样例输入 #1
100 3 5000
20 1000
90 1
110 10000
样例输出 #1
1
样例 #2
样例输入 #2
50 4 10
60 100
70 1000
80 1000
90 0
样例输出 #2
-1
提示
数据规模与约定
对于全部的测试点,满足:
- $0\le n,m,k\le 3\times 10^4$,
- $0 \leq a_i,b_i\le 2147483647$。
#include<iostream>
#include<cstdio>
#include<string.h>
#include<algorithm>
#include<math.h>
#include<cmath>
using namespace std;
#define LL long long
LL k,n,m,tot;
LL a[30019],b[30019],t;
int main()
{
scanf("%lld%lld%lld",&k,&m,&n);
for(int i=1;i<=m;i++)
scanf("%lld%lld",&a[i],&b[i]);
for(int i=1;i<=m;i++)
{
if(a[i]==0)
{
printf("%d ",i);tot++;
continue;
}
t=(LL)(k/a[i])*b[i];
if(t>=n) printf("%d ",i),tot++;
}
if(!tot) cout<<-1;
return 0;
}
[NOIP2015 普及组] 金币
题目背景
NOIP2015 普及组 T1
题目描述
国王将金币作为工资,发放给忠诚的骑士。第一天,骑士收到一枚金币;之后两天(第二天和第三天),每天收到两枚金币;之后三天(第四、五、六天),每天收到三枚金币;之后四天(第七、八、九、十天),每天收到四枚金币……;这种工资发放模式会一直这样延续下去:当连续 $n$ 天每天收到 $n$ 枚金币后,骑士会在之后的连续 $n+1$ 天里,每天收到 $n+1$ 枚金币。
请计算在前 $k$ 天里,骑士一共获得了多少金币。
输入格式
一个正整数 $k$,表示发放金币的天数。
输出格式
一个正整数,即骑士收到的金币数。
样例 #1
样例输入 #1
6
样例输出 #1
14
样例 #2
样例输入 #2
1000
样例输出 #2
29820
提示
【样例 1 说明】
骑士第一天收到一枚金币;第二天和第三天,每天收到两枚金币;第四、五、六天,每天收到三枚金币。因此一共收到 $1+2+2+3+3+3=14$ 枚金币。
对于 $100%$ 的数据,$1\le k\le 10^4$。
#include <stdio.h>
int main()
{
int k; //天数
int i,n=1,sum=0;
scanf("%d",&k);
while(k>0)
{
for(i=0;i<n;i++)
{
k--;
sum=sum+n;
if(k==0)break;
}
n++;
}
printf("%d",sum);
return 0;
}
[NOIP1999 普及组] 回文数
题目描述
若一个数(首位不为零)从左向右读与从右向左读都一样,我们就将其称之为回文数。
例如:给定一个十进制数 $56$,将 $56$ 加 $65$(即把 $56$ 从右向左读),得到 $121$ 是一个回文数。
又如:对于十进制数 $87$:
STEP1:$87+78=165$
STEP2:$165+561=726$
STEP3:$726+627=1353$
STEP4:$1353+3531=4884$
在这里的一步是指进行了一次 $N$ 进制的加法,上例最少用了 $4$ 步得到回文数 $4884$。
写一个程序,给定一个 $N$($2 \le N \le 10$ 或 $N=16$)进制数 $M$($100$ 位之内),求最少经过几步可以得到回文数。如果在 $30$ 步以内(包含 $30$ 步)不可能得到回文数,则输出 Impossible!。
输入格式
两行,分别是 $N$,$M$。
输出格式
如果能在 $30$ 步以内得到回文数,输出格式形如 STEP=ans,其中 $\text{ans}$ 为最少得到回文数的步数。
否则输出 Impossible!。
样例 #1
样例输入 #1
10
87
样例输出 #1
STEP=4
#include <cstdio>
#include <cstring>
const int S=303;//一次加法顶多多一位,所以顶多多30位,也就是130位左右。我开大一点,开到300.
int n,a[S],l;
char c[S],d[S];
inline void add()
{
for (int i=0;i<l;++i)
d[l-i-1]=c[i];
l+=2;//可能有进位,所以我们干脆在前面先多空个两位
for (int i=0;i<l;++i)
{
c[i]+=d[i];
if (c[i]>=n) c[i+1]++,c[i]-=n;
}
while (!c[l-1]) --l;//大不了多余的前导0再减回来嘛~~简化思维~~
}
inline bool pd()
{
for (int i=0;i<l;++i)
if (c[i]!=c[l-1-i]) return false;
return true;
}
int main()
{
scanf("%d%s",&n,c);l=strlen(c);
for (int i=0;i<l;++i)
{
if (c[i]>='0' && c[i]<='9') c[i]-='0';
else c[i]=c[i]-'A'+10;
}
int step=0;
while (!pd())
{
++step;
if (step>30) break;
add();
}
if (step<=30) printf("STEP=%d\n",step);
else puts("Impossible!");
return 0;
}
kotori的设备
题目背景
kotori 有 $n$ 个可同时使用的设备。
题目描述
第 $i$ 个设备每秒消耗 $a_i$ 个单位能量。能量的使用是连续的,也就是说能量不是某时刻突然消耗的,而是匀速消耗。也就是说,对于任意实数,在 $k$ 秒内消耗的能量均为 $k\times a_i$ 单位。在开始的时候第 $i$ 个设备里存储着 $b_i$ 个单位能量。
同时 kotori 又有一个可以给任意一个设备充电的充电宝,每秒可以给接通的设备充能 $p$ 个单位,充能也是连续的,不再赘述。你可以在任意时间给任意一个设备充能,从一个设备切换到另一个设备的时间忽略不计。
kotori 想把这些设备一起使用,直到其中有设备能量降为 $0$。所以 kotori 想知道,在充电器的作用下,她最多能将这些设备一起使用多久。
输入格式
第一行给出两个整数 $n,p$。
接下来 $n$ 行,每行表示一个设备,给出两个整数,分别是这个设备的 $a_i$ 和 $b_i$。
输出格式
如果 kotori 可以无限使用这些设备,输出 $-1$。
否则输出 kotori 在其中一个设备能量降为 $0$ 之前最多能使用多久。
设你的答案为 $a$,标准答案为 $b$,只有当 $a,b$ 满足
$\dfrac{|a-b|}{\max(1,b)} \leq 10^{-4}$ 的时候,你能得到本测试点的满分。
样例 #1
样例输入 #1
2 1
2 2
2 1000
样例输出 #1
2.0000000000
样例 #2
样例输入 #2
1 100
1 1
样例输出 #2
-1
样例 #3
样例输入 #3
3 5
4 3
5 2
6 1
样例输出 #3
0.5000000000
提示
对于 $100%$ 的数据,$1\leq n\leq 100000$,$1\leq p\leq 100000$,$1\leq a_i,b_i\leq100000$。
#include<bits/stdc++.h>
using namespace std;
int n;
double p,a[100001],b[100001],sum;
int main(){
cin>>n>>p;
for(int i=1;i<=n;i++){
cin>>a[i]>>b[i];
sum+=a[i];
}
if(sum<=p){//如果充电宝的能量比设备需要消耗的能量还多,那就可以一直用下去。
cout<<-1;
return 0;
}
double l=0,r=1e10;//r一定要开大一点,要不然会WA
while(r-l>1e-4){//注意精度误差
double mid=(l+r)/2;//使用时间
double num=0;
for(int i=1;i<=n;i++){
if(b[i]>=a[i]*mid){//如果本身有的能量大于去要消耗的能量
continue;
}
num+=(a[i]*mid-b[i]);//否则使用充电宝
}
if(num<=p*mid){//如果充电宝的能量够用
l=mid;//往大找
}else{//不够用
r=mid;//缩短时间
}
}
cout<<l;
return 0;
}
[NOI1995] 石子合并
题目描述
在一个圆形操场的四周摆放 $N$ 堆石子,现要将石子有次序地合并成一堆,规定每次只能选相邻的 $2$ 堆合并成新的一堆,并将新的一堆的石子数,记为该次合并的得分。
试设计出一个算法,计算出将 $N$ 堆石子合并成 $1$ 堆的最小得分和最大得分。
输入格式
数据的第 $1$ 行是正整数 $N$,表示有 $N$ 堆石子。
第 $2$ 行有 $N$ 个整数,第 $i$ 个整数 $a_i$ 表示第 $i$ 堆石子的个数。
输出格式
输出共 $2$ 行,第 $1$ 行为最小得分,第 $2$ 行为最大得分。
样例 #1
样例输入 #1
4
4 5 9 4
样例输出 #1
43
54
提示
$1\leq N\leq 100$,$0\leq a_i\leq 20$。
#include<bits/stdc++.h>
using namespace std;
const int MAXN = 250;//很吉利
int a[MAXN],sum[MAXN],f[MAXN][MAXN],d[MAXN][MAXN];
int n,maxn=-0x3f3f3f3f,minn=0x3f3f3f3f;
void dp(int p)
{
for(int i=1+p;i<=n+p;i++)
for(int j=i;j<=n+p;j++)
f[i][j]=0x3f3f3f3f,d[i][j]=0;
for(int i=1+p;i<=n+p;i++) f[i][i]=d[i][i]=0;//初始化
for(int j=1+p;j<=n+p;j++)
for(int i=j;i>=1+p;i--)//逆序枚举
for(int k=i;k<j;k++)
{
f[i][j]=min(f[i][j],f[i][k]+f[k+1][j]+sum[j]-sum[i-1]);
d[i][j]=max(d[i][j],d[i][k]+d[k+1][j]+sum[j]-sum[i-1]);
}
minn=min(minn,f[1+p][n+p]);
maxn=max(maxn,d[1+p][n+p]);
}
int main()
{
cin>>n;
for(int i=1;i<=n;i++)
{
scanf("%d",&a[i]);
a[i+n]=a[i];
sum[i]=sum[i-1]+a[i];
}
for(int i=n+1;i<=2*n;i++) sum[i]=sum[i-1]+a[i];
for(int i=0;i<n;i++)//破环成链 枚举区间
{
dp(i);
}
cout<<minn<<endl<<maxn<<endl;
return 0;
}



