霍夫变换

经典霍夫变换

参考：https://blog.csdn.net/shenziheng1/article/details/75307410

 

1换一种方式表示一条直线

在直角坐标系统，我们可以使用通常使用点斜式的方式表示表示一条直线，但是在hough变换中，我们使用的形式表示一条直线。其中r表示该直线到原点的距离，表示直线的垂线与x轴正方向的夹角。如下图所示:

 

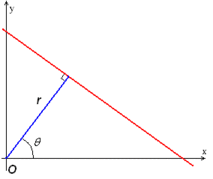
注意！！！和极坐标没有半毛钱关系！！！！！

原点到直线的距离 r = x cos(theta) + y sin(theta)

2经典霍夫变换(检测直线)

对于点P，我们计算得到过点P的n个方向的直线，通常n=180，即直线每转1°，就计算得到该直线的值。这样如果我们有m个点，对这m点都做一次计算，如果有多个点在一条直线上，那么肯定有时，有多个点的r近似等于,也就是多个点在直线上。

 

3霍夫圆检测

直线检测时，对每个点，枚举了所有过该点的直线，最后统计时发现多个点都有过该条直线时，该条直线自然被识别出来。

那么是否可以参考圆检测的思路，对点P枚举所有过点P的圆的集合，再做统计呢？

首先考虑如何表示一个圆？圆由圆心坐标和半径组成，（a,b,r）即我们有三个量。同样对所有的点找到过该点的圆集合，遍历完所有的点后，许多点都有(a,b,r)这个圆，则我们可以认为存在圆(a,b,r),但是这种方法效率较低。考虑到过点P的所有圆的轨迹实质是以(a,b)为圆心，r为半径运动的，所以如果有多个半径相同的圆的轨迹相交于一个点，那么这些点我们可以认为是在一个圆上，圆心即为交点。